Figure 1: Nitric Acid : Three Units of Oxidizing Power
The game of balancing chemical reaction equations is played according to certain rules. We will discuss the rules in a moment (section 2), but before we do that, let’s work through an example. The rules are more meaningful when we have an example to apply them to.
Here is my recommended method for balancing chemical equations that involve charge being transferred from one molecule to each other. These are conventionally called “oxidation-reduction” reactions, or “redox” reactions for short.
We are going to take the simple, direct approach, using charge – not the so-called oxidation number. We balance charge in exactly the same way that we balance atoms: the amount of charge on the LHS of the reaction must equal the amount of charge on the RHS.
|
Charge is important. Charge is fundamental. Charge
strictly obeys a local conservation law. It is worth understanding the charge-conservation law, because it has very broad applications (not just limited to chemistry). |
Oxidation number is not synonymous with charge ... not even close. The conventional “rules” for computing oxidation number have many drawbacks, as will be discussed in section 5. |
I assume you already know how to solve simple stoichiometry problems, so let me dive right into a charge-transfer scenario that is complicated enough to be interesting. I will show that my methods get the right answer – including numbers and insight – without the least bit of brain-strain.
Here’s the scenario: We expose metallic cadmium to nitric acid.
We will start by writing various less-than-optimal forms of the reaction equation, and improve them as we go along. A crude skeletal form of the intended reaction is:
| Cd + NO3– → Cd++ + NO (skeleton) (1) |
The skeleton in equation 1 is the form commonly encountered in textbooks. According to some peculiar convention, we are supposed to imagine that in front of each term in the equation, there is an invisible “implicit” coefficients with an as-yet unknown value. This conflicts with the sensible, well-established algebraic convention that you can omit a factor when it is equal to unity, but not otherwise.
Experts may prefer the brevity of the skeleton, but students prefer the more-explicit form. For present purposes, it is very helpful to write the coefficients explicitly:
| a Cd + b NO3– → w Cd++ + y NO (allegedly) (2) |
where our task is to determine the value of the coefficients a, b, w, and y.
For simplicity, we rescale the equation so that the a coefficient becomes a=1. This gives us:
| Cd + b NO3– → w Cd++ + y NO (allegedly) (3) |
(Note: We reserve the right to change the scale-factor later. In fact we will do so, leading up to equation 7.)
Equation 3 is much clearer than equation 1, but still it is highly problematic. It is unbalanceable with respect to charge ... not just unbalanced, but unbalanceable. It is also unbalanceable with respect to oxygen and, as we shall see, other important elements. To make it balanceable, we must use information that was contained in the original statement of the problem, but not expressed in equation 2, including the fact that the reaction takes place in aqueous solution.
Putting these ideas together, our next (but still slightly problematic) version of the equation is:
| Cd + b (H+ NO3–) + c (H+ OH–) → Cd++ + v OH– + y NO + z (H+ OH–) (allegedly) (4) |
where we have dropped the w coefficient since it is rather obvious that w=1 (or, more generally, w=a).
One good thing about this equation is that the second term on the LHS – the nitric-acid term – can be obtained by starting with the second term in equation 1 and rewriting NO3– in terms of HNO3. This reflects the fact that you cannot obtain a bottle of NO3– from the stockroom, but you can obtain a bottle of nitric acid. A weaker argument leading to the same conclusion involves the rule of thumb that if you are trying to charge-balance a reaction in aqueous solution (especially acidic solution), you should consider the hypothesis that the negative ions are balanced by H+ ions.
Another good thing is that the LHS of equation 4 has manifestly zero charge, no matter what the coefficients may be.
Yet another good thing is that equation 4 is balanceable w.r.t charge and balanceable w.r.t the atoms.
One slight problem with equation 4 is that the OH term on the RHS comes from mis-applying the rule of thumb that if you are trying to charge-balance a reaction in aqueous solution (especially alkaline solution), you should consider the hypothesis that the negative ions are balanced by OH– ions. This is a big problem, because we do not have an alkaline solution. Equation 4 is OK from a “redox only” point of view, i.e. from a charge-balance-only point of view ... but it is not OK from a broader chemistry point of view. There will not be a lot of OH– ions running around. Therefore it makes much more sense to charge-balance the Cd++ ions using NO3– ions, which are by far the most-abundant negative ions available in this situation.
Our almost-final representation for the current example is:
| Cd + b (H+ NO3–) + c (H+ OH–) → Cd++ + x NO3– + y NO + z (H+ OH–) (5) |
The last detail we need to deal with is the fact that the reaction takes place in aqueous solution. Therefore the coefficients b and z are enormous positive numbers. In practice, what we care about is the difference between these two numbers, one way or the other: If the overall reaction consumes H2O, we care about c−z, whereas if the overall reaction produces H2O, we care about z−c. A little thought shows that the latter is what happens in this case. Hint: If you cover the z term in equation 5 with your thumb, what’s left has no H at all on the RHS, so that would be a bad thing. Covering up the b term has no such obvious downside. Therefore we define z’ (pronounced “z prime”) via z’ = z−c and rewrite our equation as:
| Cd + b (H+ NO3–) → Cd++ + x NO3– + y NO + z’ (H+ OH–) (6) |
The coefficients in equation 6 can be determined using the usual methods – such as Gaussian elimination – as discussed in reference 1.
I emphasize that when you do the math, you must write an equation expressing equal amounts of charge on the two sides of the reaction. This is profoundly analogous to the equation expressing equal amounts of, say, nitrogen on the two sides of reaction. In this case, charge-balance immediately tells us that x = 2.
Using Gaussian elimination, I get b = 8/3, x = 2, y = 2/3, and z’ = 4/3. Then by changing the scale factor, scaling things up by a factor of 3, we can write our equation as:
| 3 Cd + 8 (H+ NO3–) → 3 Cd++ + 6 NO3– + 2 NO + 4 H2O (7) |
which is our final answer. It is even easier to verify that it is to derive. Please take a moment to convince yourself it is balanced w.r.t cadmium, oxygen, hydrogen, nitrogen, and charge.
Equation 7 is correctly balanced, in the narrow sense of the word. However, it is not in lowest terms, because it has NO3– on both sides. Sometimes it is worth writing equations in lowest terms (as in equation 8, below) ... but sometimes non-lowest terms have their advantages. One advantage to equation 7 is that each side is separately charge-balanced. Another advantage is that the two items on the LHS – cadmium and nitric acid – are items you can actually obtain from the chemistry stockroom.
To my eyes equation 7 makes some aspects of the chemistry more readily apparent ... but you are not obliged to do it that way. If you find equation 7 too unconventional, you are free to use equation 8, which expresses the same reaction in conventional lowest terms.
| 3 Cd + 8 H+ + 2 NO3– → 3 Cd++ + 2 NO + 4 H2O (8) |
There are at least two viewpoints, two ways of thinking about what a chemical reaction equation means.
This viewpoint is relevant whenever you have a reaction that starts out with pretty much 100% reactants and then goes to completion, producing pretty much 100% products.
According to this viewpoint, the process of balancing a chemical reaction equation involves several steps. These include:
The linear-algebra step is important, because we want our equation to be a faithful representation of what actually happens in the lab. Mother nature enforces the conservation laws in the lab, and we use linear algebra to enforce the same constraints on our equations. In a chemical reaction with N kinds of atoms present, there are N+1 conservation laws. Charge is conserved, and each type of atom is separately conserved.
The constraint-satisfaction step is also important, because there is a another law of nature, a law that says you cannot have a negative amount of any reactant or product.
These steps are sometimes performed out of order. That is, sometimes backtracking and iteration are involved. For example, the constraint-satisfaction step might tell you that you need to go back and rewrite the equation. We have already seen an example of this. If we had written equation 5 with an amount c−z of water on the LHS, the linear algebra would have assigned a negative value to c−z. That is the world’s smallest problem. It is super-easy to fix. It is telling us we really have an amount z−c of water on the RHS (rather than c−z on the LHS).
This viewpoint is relevant when you have a reaction that does not go to completion. There is some nontrivial amount of every species present, and we are primarily interested in the changes i.e. the variations in the amounts.
To make this idea explicit, we can rewrite equation 6 as follows:
| (9) |
The point here is that most of the atoms are spectators. They are represented by the zeroth-order variables a0 through z0. They are present, but they do not participate in the reaction. Because they are present before and after the reaction takes place, the conservation laws have got nothing to say about them.
We therefore turn our attention to the first order variations, represented by the quantities δa through δz. equation 9 is interesting useful, because it expresses a set of constraints on these variables.
The steps to be followed in this situation include:
There is no positivity constraint on the first-order variations δa through δz. The constraint only applies to the zeroth-order quantities a0 through z0. The physics is the same. You just have to realize that a0 is huge and |δa| is small, so a0 + δa is positive no matter whether δa is positive or negative.
The minus signs in equation 9 have been artfully arranged to make the linear-algebra part of this problem exactly the same as the linear algebra we did to derive equation 7. This is not important. It gives positive values for all the deltas, but there is no law of nature that requires this.
The we can put the values together to form a vector [δa, δb, δw, δx, δy, δz]. This is a vector in the tangent space. It tells how things change when the reaction proceeds by an infinitesimal amount.
| Sometimes it is OK to gloss over the distinction between the zeroth-order viewpoint and the first-order viewpoint. | Sometimes the distinction is important. |
| Because the linear algebra is the same in either case, if/when you are focusing on the linear algebra part of the problem, you don’t actually care whether you are solving the zeroth-order problem or the first-order problem. | Sooner or later you are going to run up against the positivity constraint. |
| The tangent vector tells you what’s going on locally. To first order, everything is linear. | There are limits to how far you can extrapolate the linear behavior. Real life is definitely nonlinear. |
To my eyes, equation 7 is a reasonable description (at the black-box level) of what “really” happens. It says we start out with metallic cadmium and nitric acid. We wind up with cadmium nitrate and water, with the evolution of nitric oxide gas.
One aspect of this equation makes students do a double-take, namely the ratio of 8 moles of acid to 3 moles of metal. That is a peculiar ratio. One might reasonably ask what is the physical significance of this.
The answer is that the nitric acid is playing two roles. For each three moles of metal, we need
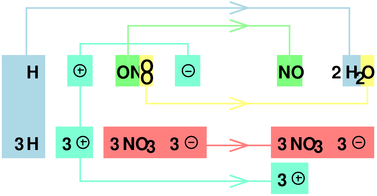
This point is discussed in much greater detail in connection with figure 1 in section 3.2.
For each nitrate ion that is is consumed, there are three acid molecules are basically just proton donors. They could be replaced by more-or-less any other acid, and the reaction would look the same from a redox point of view.
By the way, this sheds quite a bit of light on the oft-misunderstood principles behind the action of aqua regia. You can’t dissolve gold with just HCl, because although that’s a fine acid, it isn’t a particularly powerful oxidizing agent. (It will oxidize zinc, as discussed in connection with equation 12, but not gold.) Conversely, you can’t attack dissolve with just HNO3, because although that’s a fine oxidizing agent, the formation of gold nitrate is not energetically favorable. Gold chloride is energetically more favorable. (Another way to dissolve gold is to use HCl plus electricity, in an electrolytic cell.)
I claim that equation 7 is easy to derive and easy to interpret. It seems advantageous from the conceptual, procedural, and pedagogical viewpoints. It shows we don’t need to bother figuring out the “oxidation number” of the nitrogen or other atoms. We just balance the equation w.r.t charge and w.r.t atoms.
As mentioned in section 3.1,
It is instructive to examine why nitric acid is such a good oxidizing agent.
By way of preliminaries, consider the following scenario: Imagine what would happen if an NO3– ion were converted to NO gas and O2 gas. That would leave behind one unit of negative charge ... so it would be acting as a reducing agent, not the expected oxidizing agent.
Of course that’s not quite what actually happens. Part of that scenario is correct, but part is not. Instead, when the NO3– ion gives up oxygen, it isn’t energetically favorable to form an O2 molecule. Instead, especially in acidic solution, each oxygen atom grabs a couple of H+ ions and thereby forms an H2O molecule, leaving behind four units of positive charge. We still have to account for the negative charge mentioned in the previous paragraph, which leaves +3 units. The process is diagrammed in figure 1. The bottom line is that one unit of nitrate has three units of oxidizing power.
It is easy to understand the oxidation of Cd as a Cd atom giving up electrons, whereas the reduction of nitrate is much more complicated.
Since three of the four nitrate ions in figure 1 are little more than spectators, we can write a more abstract and more general expression:
| NO3– + 4 H+ + 3 e– → NO + 2 H2O (10) |
Of course figure 1 and
equation 10 are only half-reactions. It
cannot occur by itself, since it shows three units of disembodied
charge lying around on the RHS. A half-reaction makes sense only in
conjunction with another half-reaction. In this case, the other half
is the oxidation of Cd to Cd++.
In the literature you can find long lists of half-reactions, balanced w.r.t atoms and charge. Usually the energy balance is included also, e.g.
| NO3– + 4 H+ + 3 e– → NO + 2 H2O + 0.96v (11) |
where the reduction potential is given in volts. The official SI abbreviation for volt is capital V, but here we write it as lower-case v, to avoid confusion with vanadium. Beware that a volt is one joule per coulomb of electrons. So if you want to find the standard molar energy of the reaction, you need to convert coulombs to moles, and then multiply by 3, because in equation 11 there are 3 moles of electrons per mole of reaction (i.e. per mole of “→”).
See e.g. reference 2 for a list of half-cell reactions and their standard reduction potentials.
In an electrochemical cell, there will be one half-reaction occurring at one electrode, and another half-reaction occurring at the other electrode. In this case, the half-cell reactions have real physical significance.
In contrast, if the reaction proceeds without electrochemistry (just by mixing the reactants), picking the reaction apart into half-reactions is arbitrary and optional. Sometimes it is a labor-saving device, and sometimes not. Sometimes it is useful in conjunction with the direct approach, as exemplified by this document: First you balance the equation using the direct approach, then you go back and try to understand it from the half-reaction viewpoint also.
The point of writing equation 11 is that we are making a prediction: We expect that nitrate will behave this way (evolving NO and giving us three units of oxidizing power) independent of which acid(s) supply the four required protons (over a moderately wide range), and independent of what gets oxidized (over a moderately wide range).
This prediction means you can understand more reactions with less work. If you know N oxidation half-reactions and M reduction half-reactions, then (roughly speaking) you can understand MN reactions with only M+N work.
On the other hand, if you are interested in balancing just one given reaction, you don’t need to do MN work or even M+N work ... it is easier to just balance the given reaction directly, using the methods discussed here.
The discussion in this subsection assumes the overall reaction happens in one place (not separated as in an electrochemical cell).
Consider the contrast:
| Energy and conservation of energy are primary and fundamental. | Half-cell reduction potentials are a sometimes-useful elaboration. |
Half-cell reduction potentials are one way, but not the only way, to calculate the energy of a reaction.
Similarly:
| Charge and conservation of charge are primary and fundamental. |
Half-reactions are a sometimes-useful elaboration. Oxidation numbers (as discussed in section 5) are an optional elaboration of very dubious usefulness. |
Half-reactions are one way, but not the only way, of balancing a reaction w.r.t charge. Tabulated half-reactions are always already charge-balanced, so anything you construct as a linear combination of two or more of them will also be charge-balanced. On the other hand, as we saw in section 1, it is straightforward to balance an equation directly, without going anywhere near the half-reaction concept.
Oxidation numbers are another way, but not the only way, of balancing a reaction w.r.t charge. As we saw in section 1, it is straightforward to balance an equation directly, without going anywhere near the oxidation-number concept.
The half-reaction concept and the oxidation number concept are mutually independent. You don’t need oxidation numbers to discuss half-reactions, nor vice versa.
Transition metals can change their electron configuration.
For example, the cuprous ion (Cu+) has configuration [Ar]3d104s0, while in contrast the cupric ion (Cu++) has configuration [Ar]3d94s0.
A change in electron configuration has direct physical significance, including the color of ions in solution, magnetic properties, et cetera.
There are several different ways of looking at this situation, each with its own terminology. As applied to a transition metal ion, talking about charge is equivalent to talking about oxidation number. This is not a problem.
One also very commonly hears the cuprous ion called monovalent, while the cupric ion is called divalent. However, there is no consensus as to whether the ancient idea of valence corresponds to charge or to coordination number (or whatever). Once upon a time there was an attempt to patch this up by talking about primary valence versus secondary valence ... but the current trend seems to be to downplay the whole notion of valence in favor of more modern, more precise terms (i.e. charge and coordination number).
The notion of oxidation numbers can be used to calculate the charge balance of a reaction. This method is undoubtedly better than nothing. But the discussion should not stop there, not even for a moment. “Better than nothing” is not the relevant criterion!
In many cases, including this case, we have a choice of formalisms. We should compare each formalism to each of the others, comparing them in terms of convenience, accuracy, generality, et cetera.
The question here is not whether the oxidation-number concept is “wrong” or “unusable”. The question is, why bother? Why should you bother learning two concepts (charge and oxidation number) when learning one concept (charge) suffices?
All available evidence suggests that if your goal is to understand chemical reactions of the sort that are relevant in a first-year chemistry course, then you don’t need to bother with the oxidation-number concept or the oxidation-number “rules”.
Instead, the two concepts that are important are:
Consider the contrast:
| These two concepts are completely non-arbitrary. They have direct physical significance. They have lasting value. The concepts of conservation in general, and conservation of charge in particular, have a very wide range of applications. | The notion of oxidation number is artificial. It has no direct physical significance. Many of the oxidation-number rules are arbitrary. The concept is applicable to chemistry only. |
There are various ways of stating the oxidation-number “rules”, but almost always the first rule is:
That rule is easy to remember, and has an obviously-sensible physical interpretation.
However, things go downhill from there. In order for the “rules” to be useful at all, they must assign oxidation numbers to each element in polyatomic species such as NO3– and NO. The problem is, for the purpose of balancing an equation w.r.t charge, we don’t need to know what’s going on within the molecule – only the total charge matters, and we already know that. The total charge of NO3– is manifestly -1, and the total charge of NO is manifestly zero.
For other purposes, you might really want to know what is happening within a polyatomic molecule. For example, you might want to predict whether the electron configuration will be paramagnetic or not, and you might want to predict whether the molecule will be polar or not. However, oxidation numbers do not tell you any such thing. The “rules” for assigning oxidation numbers within a polyatomic molecule are:
For example, according to the “rules”, carbon can have any oxidation number from -4 to +4 inclusive. (The extremes are illustrated by CH4 and CCl4, respectively.) The number is not telling you anything about the charge on the carbon atom, or bond strength, or any other observable, non-arbitrary quantity.
In light of all these drawbacks, you may be wondering how oxidation numbers could have any pretense of usefulness. The answer is that only changes in oxidation number contribute to the charge balance, so you can make pretty wacky oxidation-number assignments and still be able to balance the reaction equation, provided you consistently make the same wacky assignments.
In any case, it remains very much open to question whether there is any reason to bother learning the oxidation-number concept. Every example I can think of can be handled just fine using the direct approach as discussed in section 1 ... balancing charge per se, without bothering with oxidation numbers. I don’t know what is the oxidation number of the nitrogen atom in the nitrate ion, and I cannot imagine why anybody would want to know it.
The charge-balance concept is easy to learn, easy to remember, and easy to use. Just convince yourself that charge is conserved, and therefore charge on the two sides of the equation must balance. That’s all there is to it. You perform the balance w.r.t charge on exactly the same footing as the balance w.r.t atoms.
Charge-balance appears to be simultaneously more simple, more profound, and more practical.
As you may have noticed, I recommend using the term “charge balance” in preference to “electron balance”. This is not super-important, because in any chemistry situation (but not more generally) each of those implies the other ... so experienced chemists would be within their rights to consider them to be conceptually equivalent. The wrinkle is that charge can be either positive or negative, while electrons are always negative. Therefore in cases where a positive charge is required, students may have a hard time visualizing it as a negative number of electrons.
The laws marked with a (*) are valid during chemical reactions, but not more generally; this defines the distinction between chemistry and nuclear physics.
If you want, you can remove the (*) restrictions as follows: The electron-conservation law is an approximation to a more general law (conservation of lepton number). Similarly the proton-conservation law is an approximation to a more general law (conservation of baryon number). The following are valid without without limitation, for all practical purposes:
I emphasize that none of the laws on this list should be considered a consequence of the others. Each stands on its own independent fundamental foundations.
As a consequence of the aforementioned laws, we can derive a couple of very useful corollaries,
Beware that some people who ought to know better throw around the term “mass balance” whenever they see a conservation law, even when it’s one of the other conservation laws. Remember: There are lots of independent conservation laws.
Also, beware of another weird bit of conflicting terminology: Chemists use roman numerals in parentheses to designate oxidation number, e.g. Cu(I) and Cu(II). This is called the Stock system. Meanwhile astronomers use roman numerals without parentheses to designate the ionization state, i.e. the charge, offset by one, so that O-III means doubly-ionized oxygen, O++ – which is found in outer space, but not commonly found in bottles in the chemistry stockroom.
Last but not least, beware that “oxidation” has two very different technical meanings. Thoughtful experts freely use the word in both ways ... sometimes even in the same sentence!
| In the context of redox reactions, oxidation means transfer of electrons. An oxidizing agent “pushes” electrons and is reduced by the reaction, while reducing agent “accepts” electrons and is thereby oxidized. | In a far older (and still correct) sense, oxidation means transfer of oxygen. An oxidizing agent “pushes” oxygen and is reduced by the reaction, while a reducing agent “accepts” oxygen and is thereby oxidized. |
As an example where this meaning applies (and the other does
not), consider attacking zinc with hydrochloric acid:
where we see that the zinc is oxidized, even though there are no oxygen atoms anywhere in sight. Actually, there is a wide class of acids that can serve the same purpose, so there is some value in writing a more abstract reaction:
|
As an example where this meaning applies (and the other not), consider the oxidation of SO3= to form SO4=. This involves the transfer of oxygen, but no transfer of charge. |