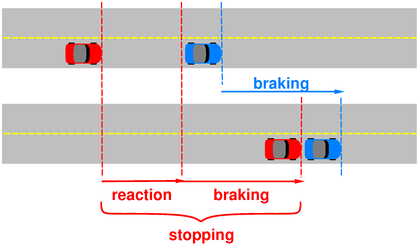
Figure 1: Car Following Similar Car
The process of stopping your car has two main components: reaction and braking. Loosely speaking
| stopping = reaction + braking (1) |
The distance your car travels during the reaction time is proportional to your speed. That’s just distance=rate×time.
The distance required for braking scales like the square of your speed. That makes sense, because at high speeds it takes more time to stop, and during that time you are moving faster. Reference 1 contains some analysis and some useful data. (See also reference 2 for a general discussion of scaling laws.)
One important special case arises if you are following another car with similar performance to yours, and it suddenly slams on its brakes. In this case, you don’t care so much about braking distance, because the other car will have a braking distance also. The main factor that determines whether you will have a rear-end collision is just reaction time. This situation is illustrated in figure 1. You are driving the red car. The top part of the figure shows the situation at the moment the blue car slams on its brakes. The bottom part of the figure shows the situation after both cars have come to a stop.
However, it must be emphasized that this car-following-car scenario is not the only case you need to worry about. As a first example, if you are in a truck following a sports car, the car can stop significantly more quickly than you can, so you need to account for your braking distance as well as your reaction time. As a second example, consider the “discovered threat” scenario as illustrated in figure 2. There is a moose in the road, or some other obstruction. You can’t see the obstruction, because the blue car is blocking your view. The blue car doesn’t need to brake; it just swerves around the moose. You however are unable to swerve because of oncoming traffic (the orange car) and/or other factors. In this scenario, you need the full stopping distance (reaction plus braking).
Other “discovered threat” scenarios arise if you come around a bend in the road and see a threat that couldn’t previously be seen, or if a creature or vehicle suddenly lunges from the side of the road into your lane.
Many years ago I actually experienced a situation like this. I was able to maneuver my way out of it, with no damage or injuries, but it was a close call, much too close.
Human reaction time for tasks like this is about 1.6 seconds (reference 3). That means that if you follow the “three-second rule” as found in reference 4, you will be able to handle the special case of car following similar car, with a reasonable margin of safety.
However, the “three second rule” is nowhere near being enough to handle a discovered-threat situation. It is not enough even at 30 mph, even with no margin of safety. It is less than half what you need at 60 mph, even with no margin.
I am very disappointed in the way some driver-safety courses tout the “three second rule” as if it were the solution to all problems, without mentioning (let alone emphasizing) its limitations.