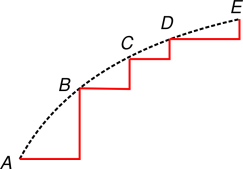
Figure 1: Reversible Approximation to an Irreversible Path
This section describes a typical presentation of classical thermodynamics.
One of the central goals of classical thermodynamics is to be able to describe heat engines, and in particular to describe how much useful work a heat engine can perform under given conditions.
The usual presentation starts by defining a notion of temperature. This can be merely asserted (based on experience or whatever) ... or it can be derived from the zeroth law. The classical version of the zeroth law says that equilibrium is a partial equivalence relation. That is to say, equilibrium is both symmetrical and transitive.
Note that an ordinary equivalence relation would be reflexive as well as symmetrical and transitive.
- Reflexive: A must be equivalent to A, always.
- Symmetrical: If A is equivalent to B, then B must be equilibrium with A.
- Transitive: If A is equivalent to B and B is equivalent to C, then A must be equivalent to C.
Since equilibrium lacks the reflexive property, it is only a partial equivalence relation. That is to say, we cannot assume that A is in equilibrium with itself or with anything else.
Maxwell (1872) emphasized the transitive property of equilibrium. Usually the symmetric property is taken for granted.
Given this partial equivalence relation, you can prove that there must be some state-variable that is the same across any set of systems in equilibrium. The variable we call “temperature” is the canonical example of such a variable. (We shall see, however, that in certain extreme cases, inverse temperature is a slightly better way of labeling equilibrium states.)
The notion of energy is inherited from previous experience with non-thermal dynamics. Ditto for mechanical state-functions such as pressure and volume.
Given a notion of temperature and a notion of energy, the classical procedure is to define entropy as follows:
| (1) |
where the integral is taken along some reversible path Γ.
The second law is then invoked to say that the integral depends only on the endpoints of the path. To say the same thing the other way, if we had a path Γ1 from state A to state B, and another path Γ2 also from state A to state B, if the integrals were not the same we could make a perpetual motion machine using a cycle that goes forward along path Γ1 and then backward along path Γ2.
Now that we know the integral depends only on the endpoints, we know that the entropy S must be a function of state.
The problem with equation 1 is that at this stage of the derivation, the definition of entropy only applies to states that can be reached by reversible paths, and indeed by reversible paths that are in equilibrium at every step along the way (so that temperature is well defined).
This is a huge hole in the plot. Any reasonable theory of thermodynamics must be able to deal with irreversibility.
Consider for example Rumford’s epochal experiments, which involve irreversible frictional heating. This is shown schematically by the dotted black line in figure 1. We might know that the final state E has more entropy than the initial state A, but we don’t know whether the increase of entropy occurred between A and B, or between B and C, or whatever. If we are unable to evalue the entropy of some state (such as B, C, and/or D) we cannot achieve the central goal of thermodynamics. That is, we cannot predict now much useful work could be performed by a heat engine using such a state as one if its inputs. Classical thermodynamics must be considered seriously incomplete unless we can close this hole.
The usual band-aid for this problem goes like this: Even though Rumford’s process was irreversible, we can approximate it by a succession of reversible steps. Recall that in figure 1, the true irreversible path is shown as a black dotted line. It involves boring the cannon with a dull tool. Meanwhile, however, we are supposed to imagine that Rumford could have bored the cannon with a much sharper tool, causing the cutting process to be thermodynamically reversible or nearly so. Meanwhile, the equivalent amount of heating of the cannot could have been achieved reversibily, by reference to a special heat bath, a slush fund of entropy as it were, using perhaps an artful combination of procedures such as isentropically compressing the heat bath while it is contact with the cannon, causing a reversible flow of entropy into the cannon.
The amount of entropy that came out of the slush fund (in theory) is a measure of the irreversibility of the process (in reality).
A possible combination of reversible cutting steps and reversible heating steps is shown by the red lines in figure 1.
The implicit (or sometimes explicit) claim is this:
Any irreversible process can be approximated as closely as necessary by a sequence of reversible steps, and in this way we can use equation 1 to define the entropy in any possible situation.
This claim is important, because it is needed to close the hole in the plot. Otherwise, we would be unable to evaluate the entropy of the intermediate states in figure 1, and our theory would be seriously incomplete.