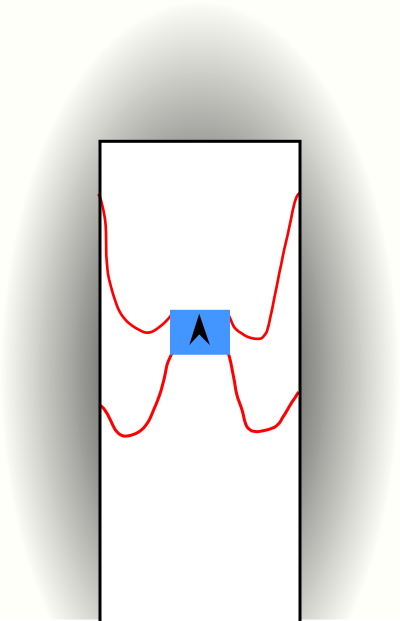
Figure 1: The Dirac String Trick
Consider a situation where rotating something by 720∘ is in some sense the same as no rotation at all. You might think that a 360∘ rotation would work just as well – but this is not true!
Build the simple apparatus shown in figure 1. That is, start with a piece of cardboard or some such, about 10 or 15 cm on a side. Mark one side with an arrow or other symbol so that the card has a definite “front” and a definite “up” orientation. Attach a string to each of the four corners of the card. Attach the other end of each string to a door frame, as shown in the figure. Make the strings long enough to provide a reasonable amount of slack.
Now flip the card over twice. That is, flip it two full turns in the same direction, turning it around the horizontal axis. This puts a double twist into each pair of strings. Now take the two strings on your left and pass them around the back of the card. Then take the other two strings and pass them around also.
This removes the twist.
The remarkable thing is that if you flip the card over only once, only one full turn, you cannot remove the twist. The maneuver that we previously used removes two units of twist, so if you start with only one, you wind up with one unit of twist in the opposite direction.
The demonstration works equally well if you rotate the card around a vertical axis, or any other axis.
It is traditional and logically sufficient to perform this demonstration with only two strings (as in reference 1). A three-string version is featured in reference 2. It can also be performed using just one link, if it’s a belt or something similar that makes it easy to tell whether it’s been twisted (reference 3). It can even be done with no strings at all, using a cup of water (reference 4). Some additional mechanisms are described in reference 5.
All things considered, I prefer the 4-string version, especially when I am performing for an audience.
In quantum mechanics there are some objects for which a 2π rotation causes the wavefunction to change by a factor of −1. An additional 2π (for a total of 4π) returns the wavefunction to where it started. Objects in this category are called spinors. A spin-½ particle such as an electron is in this category. All that is very abstract and mathematical and quantum mechanical. It is remarkable to see something similar happening in a situation that is completely classical, macroscopic, and tangible.