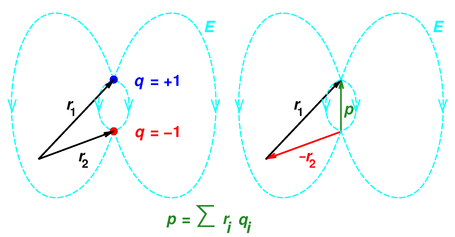
Figure 1: Dipole-Moment Vector based on Position Vectors
The electrical dipole moment is a vector. In almost all situations, it is defined as:
| (1) |
with no minus signs in the definition. The sum in the second line runs over all charged particles involved; the vector ri is the position of the ith particle, and qi is its charge. This is the definition used in reference 1 and in every physics book I know of.
As another way of saying the same thing, the dipole moment is also the first moment of the charge distribution, i.e. the first term in the multipole expansion. Contrast this with the zeroth moment (equation 6).
The only known exception to equation 1 arises sometimes in introductory chemistry classes. As discussed in section 2, some folks diagram their dipole moments in such a way as to suggest that there should be a minus sign in front of the RHS of equation 1. This is never a good idea.
We are going to stick with equation 1 as it stands, because (a) as we shall see, there are good technical reasons for it, and (b) it is conventional in every field of science and engineering, including physics, advanced chemistry, and even sometimes (albeit not always) introductory chemistry.
This definition implies that in simple cases, the dipole moment vector is directed from minus charge and towards positive charge. This is related to the fundamental and non-controversial idea that the position vector of a point is directed from the origin towards the point in question. This relationship is shown in figure 1.
You can see that the position vectors are subtracted in the usual way, namely by reversing r2 and then adding +r1 and −r2 tip-to-tail.
The result is independent of the choice of origin if the system has overall charge neutrality. (Non-neutral systems are discussed in section 3.)
Let’s be clear:
We should not be too surprised that the direction of the electric field vector is opposite to the direction of the dipole moment vector. The oppositeness is related, fundamentally, to the fact that there is a minus sign in the principle of virtual work:
| (2) |
(where F is the force, and U is any potential energy, electrical or otherwise). This minus sign is built in to our most fundamental notions of force and of “height” of potential. You cannot make this minus sign go away just by wishing. The same minus sign shows in the formula relating electric field to electric potential, i.e. equation 4.
Not coincidentally, the direction of the dipole moment shown in figure 1 is consistent with the definition of “moment” (as in quadrupole moment and other multipole moments) and “moment” (as in torque) used throughout the science and engineering community. Equation 1 is consistent with the usual formulas for the energy of a dipole in an applied electric field.
In particular: if/when the situation can be described by an electric potential Φ, the energy is
| Energy = |
| qi Φi (3) |
which has no minus signs in it, whereas the universally-accepted formula for the electric field associated with a potential does have a minus sign:
| E = − ∇ Φ (4) |
Combining these and expanding to first order we find
| (5) |
valid provided the distribution is charge-neutral overall ... and provided all the charge that contributes to the dipole p is packed sufficiently close together and the electric field is sufficiently gradually varying (as a function of position) that we can treat the field as locally uniform.
The non-neutral case is covered by equation 12.
In some chemistry books, especially at the introductory level, when diagramming polar molecules, it is common to find arrows pointing the other way, i.e. away from the positively charged end of the molecule and toward the negatively charged end of the molecule.
When this is done, there is some chance that they will warn you by putting a “+” sign on the tail of the arrow:
There are several inconsistent “just-so stories” purporting to explain the origin and meaning of these arrows. Here are some of the arguments, along with my counterarguments.
| One “explanation” points out that the arrow in figure 2 points in the same direction as the electric field in that part of the molecule. | I suppose that’s OK, provided you don’t call that arrow the dipole moment. Call it something else instead. (I don’t know what.) The real dipole moment vector is supposed to tell us about the location of the charge. It is not supposed to tell us directly about the field. Note that the dimensions and SI units of the dipole moment have to do with charge×distance … not field. You would need a factor of polarizability (є) somewhere to get dimensions of field. Just because you are accustomed to seeing field vectors pointing away from the positive charge doesn’t mean all vectors point away from the positive charge. |
| Another “explanation” argues that the arrow in figure 2 doesn’t represent charge at all, but instead represents the displacement of an electron, as it was donated from the now-positive end of the molecule toward the now-negative end. | I don’t understand why they would put a “+” sign on the end of such an arrow. It makes no sense to talk about the motion of electrons and then talk about conventional charge (i.e. positive charge) in the same breath. |
| It might be sorta nice to have a plus sign in front of p in equation 12c. | It is incomparably nicer to have a plus sign in front of p in equation 12b, which is the more usual way of writing the Taylor series. |
| In some cases, the chemistry teachers learned it that way, so they’re going to teach it that way, whether it makes sense or not. | The main reason introductory texts can get away with drawing the arrows backwards is that in 99% of the introductory-level chemistry applications, the direction of the arrow doesn’t matter anyway. It’s just something learned by rote, with no observable consequences. That means that other than stubbornness, there is no reason to keep drawing backwards arrows. People who care about the direction draw the arrows as in figure 1. People who don’t care shouldn’t make a fuss about it. |
There is confusion in the chemistry community, because in some situations, especially in advanced chemistry or physical chemistry, the direction does have observable consequences, and it becomes necessary to draw the dipole moment properly, as in figure 1.
At the very least, if you insist on drawing something like figure 2, you should warn people that your arrow is opposite to the conventional dipole moment vector.
It would be even better to always draw the dipole arrow properly, pointing to the positive charge as in figure 1, without any “+” sign on its tail. It is hard to imagine any significant downside to doing this.
We now consider systems with nonzero total charge Q:
| (6) |
This Q can be called the overall charge, or the net charge, or the total charge, or simply “the” charge. It is also the zeroth moment of the charge distribution. Contrast this with the dipole moment (equation 1), which is the first moment of the charge distribution.
For a system with nonzero charge Q, we can define the center of charge:
| (7) |
We remark that this is closely analogous to the usual definition of center of mass, for any system with nonzero total mass M:
| (8) |
If the system has nonzero Q, we need a more careful definition of electric dipole moment:
| (9) |
where rref is some reference point. For a neutral system, the value of p is independent of the choice of reference point, so equation 9 reduces to equation 1, as you can easily verify.
In many cases, such as when asking about “the” dipole moment of the proton, it would be nice to arrange it so that “the” dipole moment is a property of the system, independent of the choice of origin.
In order to do that, we need to pick a physically-significant reference point to use in equation 9. In particular, we need to pick a reference point attached to the system. That ensures that if we measure the charge distribution relative to some origin, and measure the reference point relative to the same origin, the choice of origin will drop out (even though the choice of reference point does not drop out).
You might be tempted to choose the center of charge (as defined by equation 7) as the “natural” reference point for such calculations, but if you try it you will discover that the dipole moment identically vanishes.
The conventional choice of reference point is the center of mass (as defined by equation 8). That gives us:
| (10) |
which is no longer a purely electrical property of the system; perhaps it should be called the electro-inertial dipole moment or something like that. It is nearly as much a function of the mass distribution as of the charge distribution, as we can see from the following:
| (11) |
This pcm (usually called p for short) is what people mean when they talk about “the” dipole moment of the proton, for instance in reference 2.
We can generalize equation 5 to the case of a non-neutral distribution as follows:
|
where Φ and E are evaluated at the location rref. This equation makes sense: It has a zeroth-order term and a first-order term. The zeroth-order term takes care of the unbalanced charge Q, and the first-order term is just like equation 5.