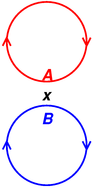
Figure 1: Rotating Hoops
In classical physics, mass is the “source term” that gives rise to the Newtonian gravitational field. In contrast, in general relativity, there are multiple source terms, including potential energy, kinetic energy, stress, pressure, and of course mass.
The way in which general relativity combines the various source terms contribute is not entirely trivial, as illustrated by the following puzzle:
Consider the following scenario: Isolated in outer space we have two massive circular hoops, both rotating the same way, arranged as shown in figure 1. Symmetrically midway between them we have a test particle (x). At point A, the upper hoop is moving right-to-left. At point B, the lower hoop is moving left-to-right. Points A and B are particularly relevant, because they are nearest to x and therefore make the largest contribution to the gravitational field at x.
This is happening in outer space; there are no relevant fields except the gravitational field of the hoops. It’s obvious by symmetry that there is no net gravitational force on x.
Observer Alice is comoving with point A. She knows the invariant mass of the hoops; everybody agrees on that. She reports that nearby parts of the upper hoop are not moving. The nearby parts of the lower hoop (point B) are moving at high speed. Therefore they have kinetic energy, which is one of the “source terms” for the gravitational field. Also she reports that the density of the lower hoop near point B has an increased density, due to the FitzGerald-Lorentz contraction. Therefore, she is tempted to predict that the test particle will accelerate downward, toward point B.
Meanwhile, observer Bob is comoving with point B. He goes through the same steps. He is tempted to predict that the test particle will accelerate upward, toward point A.
It should be obvious by symmetry that both temptations are wrong. But why are they wrong? Where did they go wrong? I’ll leave this as a puzzle for now.
This is not an elementary puzzle. Newtonian physics doesn’t suffice. Special relativity doesn’t suffice. You have to do the general relativity, and you have to do it right.
Usual jsd puzzle rules apply: Everything I’ve said here is true and non-misleading, to the best of my knowledge. But obviously I haven’t told you everything; for instance I haven’t told you the answer. This isn’t a word game; solving the puzzle requires understanding the physics, not finding tricks or twists in the statement of the puzzle.