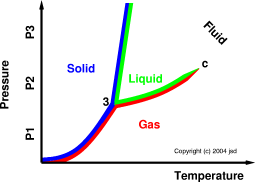
Figure 1: Phase Diagram
Consider the contrast:
| Under some conditions, we can observe that a substance starts out solid at low temperature, then melts when we raise the temperature. The liquid then evaporates when we raise the temperature some more. We have all seen H2O exhibit this behavior. | Under other conditions, and perhaps a different choice of substance, the liquid phase is skipped, and the substance passes directly from the solid to the gas. This is called sublimation. Dry ice, CO2, is a familiar example. |
We can get the lay of the land by referring to figure 1. Suppose we choose to maintain a constant pressure P1 and gradually increase the temperature (starting from a sufficiently low temperature). We observe only one phase transition: We pass directly from the solid phase into the gas phase, which is called sublimation.
Next, we select a constant pressure P2 and gradually increase the temperature. There are two phase transitions: We first pass from the solid phase into the liquid phase, which is called melting, and then we pass from the liquid phase into the gas phase, which is called evaporation.
Finally, we select a constant pressure P3 and gradually increase the temperature. We are back to having only one phase transition. We pass from the solid phase into the fluid phase. This is conventionally called melting, but it could just as logically be called sublimation, because in this regime there is no distinction between liquid and gas.
Note: The term fluid applies to gases, applies to liquids, and (crucially) applies in the regions where you can’t tell whether the fluid is a liquid or a gas or both or neither, i.e. at temperatures and/or pressures above the critical point. (See reference 1 for more about this.) The only time when you can reliably distinguish between a liquid and a gas is when they coexist, and that only happens along the curve between the triple point (labeled “3” on the diagram) and the critical point (labeled “c”). As we approach the critical point, the coexistence curve just peters out, and the distinction between liquid and gas goes away.
Now that we know what happens, let’s examine why it happens. We can get a much deeper understanding of what’s happening in terms of a tradeoff between the energy E and the entropy S. (A reliable definition of entropy, and a discussion of thermodynamics in general, can be found in reference 2.) In particular, as discussed below, must pay attention to the so-called free energy, namely
| F := E − TS (1) |
Remember that F is called free energy, and this name must never be shortened to just energy. The plain old energy is denoted E.
The system is most likely to be found in the states with the lowest F values. There are good reasons for this, as discussed in section 5.
Let’s see what low-F states exist at various temperatures.
At very low temperatures, the TS term is negligible, so we expect things to settle into the form with the lowest achievable energy. That is, low F is equivalent to low E.
At high temperatures, the TS term dominates, so we expect things to settle into the form with the highest achievable entropy. That is, low F is equivalent to high S.
The gas has a significantly higher energy than the solid, because we have to pull apart lots of bonds when we convert the solid to the gas. This is just like pulling a weight upwards against gravity or some other force. Let this difference be called
| Δ Egs := Eg − Es (2) |
which is a positive number.
A more-or-less unrelated fact is that the gas also has a higher entropy. When the substance is in solid form, we know roughly where each particle is, but when the substance is in gaseous form, each particle could be anywhere in the vessel. There are untold zillions of different places it could be. The entropy is roughly the logarithm of the number of possibilities. In any case, we denote the difference in entropy by
| Δ Sgs := Sg − Ss (3) |
We can draw pictures of this. In figure 2, we can calculate the free energy as follows: We arbitrarily choose to start with the solid phase, and measure everything relative to that. To calculate the free energy of the gas phase, we go up by an amount Δ Egs to get to the point Eg, and then to down by an amount T Δ Sgs to get the final Fg value. Since the free energy of the gas is above the free energy of the solid, the solid phase is favored at this temperature.
Figure 3 represents the same system at a higher temperature. The Δ Sgs is the same of course, but the T Δ Sgs is larger. It is enough larger to push the free energy of the gas below the free energy of the solid, so we conclude that the gas is favored at this temperature.
The same principles apply when we consider the liquid. The main difference is that we have three contestants now: maybe the solid will have the lowest F, maybe the liquid will have the lowest F, or maybe the gas will have the lowest F. It all depends on the energy/entropy tradeoff.
In figure 4, the solid is favored. The liquid and the gas have higher energy, and at this temperature the entropy terms cannot make up for the energy difference.
In figure 5, the gas is favored. This is true even though the gas has a much higher energy. The trick is that the gas, under the assumed conditions, has a very high entropy. So as we raise the temperature, before the liquid has a chance to become competitive with the solid, the gas has already won the race. This is the classic sublimation scenario.
The classic melting scenario is shown in figure 6. This differs from the scenario in that we have arranged it so that the gas has less entropy than the gas in figure 5. We can arrange this by decreasing the size of the vessel. This means that whatever gas particles are produced have less room to roam, and hence less entropy. Of course the gas always has more entropy than the liquid, but not by such an overwhelming margin as in the previous scenario.
Finally, figure 7 shows what happens if we continue raising the temperature. Eventually the gas becomes favored. It has the highest entropy, so at sufficiently high temperature that will dominate, overcoming the energy disadvantage. The liquid in figure 6 evaporates.
The energy-differences shown in the figures, such as Δ Egs and Δ Els, are illustrative not quantitative. Starting with some solids such as diamond, forming the liquid requires a tremendous amount of energy, i.e. breaking a lot of very strong bonds. And these bonds involve rather short-range interactions, so once you’ve broken enough bonds to form the liquid, forming the vapor is a relatively small step.
For some other substances, such as ordinary nitrogen (N2), disrupting the solid doesn’t take very much energy. And the interaction strength falls off only moderately quickly as the distance increases. So you can have a fairly tightly-bound liquid. The molecules in the liquid are far enough apart that they can slip past each other, yet close enough to still have considerable mutual attraction, less than in the solid, but not incomparably less.
Similarly the arrows representing entropy differences are illustrative not quantitative.
We get a bonus: using the ideas of section 2, we can easily understand why dissolving something in a liquid can be expected to depress the freezing point.
We begin by assuming that the solute is vastly more soluble in the liquid than in the solid. (If this is not true, all bets are off.) This is normally the case, because a solid is supposed to have a nice regular array of bonds, and the solute would be a foreign body – it wouldn’t fit.
Meanwhile, the presence of the solute raises the entropy of the liquid. Basically you have whatever entropy the pure solvent would have had, plus the entropy of a bunch of solvent particles running around. For dilute solutions, the solute behaves pretty much as an ideal gas.
You can can guess where this argument is going: since the entropy difference between liquid and solid is greater, the downward blue arrow in figure 6 will be longer for any given temperature. Given that freezing occurs when the TΔS arrow is no longer long enough to overcome the energy penalty represented by the ΔE arrow, more ΔS means this happens at a lower T. So we have a depression of the freezing-point.
Now that we understand the freezing-point depression in terms of entropy, we can make a remarkable prediction: To a first approximation, all solutes are the same! That is, a mole of sucrose will cause the same freezing-point depression as a mole of acetone, even though the two molecules are chemically rather different. The buzzword to use here is colligative, which has the same roots and essentially the same meaning as collective ... whenever an effect depends on the amount of substance but not the nature of the substance it is called a colligative effect.
Hint: Whenever you see a colligative effect, you should suspect that entropy is what’s driving it.
Remember that for dilute solutions at least, the solute particles behave pretty much as an ideal gas, and if you’ve seen one ideal gas you’ve seen them all. Even more remarkably, we can greatly improve our prediction by noting that a mole of CaCl2 will be three times as effective as a mole of acetone, because the CaCl2 dissociates into three independent particles and therefore produces three times as much entropy.
I’ve seen lots of attempts to “explain” freezing-point depression based on some notion other than entropy ... but as far as I can tell, they’re all bogus.
Mother Nature is trying to tell you something. It’s colligative. It’s colligative! What does that tell you? You can hypothesize anything you like about
but you haven’t got a ghost of a chance of reconciling that with the observed colligative behavior.
In contrast, the heads-versus-tails entropy of a thousand dimes is identical to the heads-versus-tails entropy of a thousand pennies. The energy, area, volume, etc. are different, but the entropy doesn’t care about any of that; it only cares about how many there are. It’s colligative!
By way of analogy, suppose we are playing a dice game, rolling two dice in the usual way. Every time you roll a seven, I pay you a dollar. Meanwhile, every time I roll a deuce, you pay me a dollar. In this game you have a six-to-one advantage. This is the low-temperature game.
Now suppose we change the rules so that every time you roll the dice once, I get to roll the dice two dozen times, and you still have to pay me a dollar every time a deuce shows up. Your advantage has evaporated, and the advantage is now four-to-one in my favor. This is the high-temperature game.
So it is with thermodynamics. On a microstate-versus-microstate basis, the low energy microstates are more probable, and entropy has got nothing to do with it. But when we consider macrostates, the high-entropy macrostates are made up of huge numbers of microstates. In a situation such as figure 3, where the high-energy (gas) phase is favored, it is because the vast numbers have collected a lot of probability even though each individual microstate is improbable. Meanwhile the microstates of the solid are individually much more probable, because of their low energy, but there just aren’t enough of them to accumulate much total probability.
The free energy quantifies the probability of the macrostate, accounting for but the intrinsic probability and the multiplicity of the microstates. That’s why it is useful for solving problems such as the one discussed here.
Of course there are numerous other things the free energy is good for in other situations.