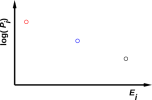
Figure 1: Three-State System with a Positive Temperature
Negative temperatures are interesting and somewhat unusual, but not impossible or paradoxical. The terminology is more peculiar than the physics.
Negative temperatures can only occur in systems where the energy spectrum is bounded above. The canonical example is a collection of spins in a magnetic field. (In contrast, you will never see a negative temperature in an ideal gas.)
Temperature, if and when it is well defined, is the inverse-negative-slope of the log-probability-versus-energy curve. The case of an ordinary, prosaic positive temperature is shown in figure 1. The corresponding case of an infinite temperature is shown in figure 2. The corresponding case of a negative temperature is shown in figure 3.
You can always define a temperature for two-state system, since you can always draw a straight line through two points. In contrast, for a system with three or more states, things get much more complicated. We must keep in mind the distinct possibility that the system will not have any meaningful temperature at all, as illustrated in figure 4.
For more on the definition of temperature, and related issues, see reference 1.
We now move to the case of more than three states.
We shall see that if you think about it the right way, you realize that inverse temperature (β, i.e. beta) is what matters.
Let’s start by taking a tour of the spin system shown in figure 5. We start at the bottom, which represents a very cold system. The inverse temperature β is large. Now, as we add gradually energy to the spin system, β declines smoothly through zero, becomes negative, and eventually becomes large and negative at the top of the thermometer.
Similarly, the temperature starts out very small for the cold system. As we gradually add energy to the system, the temperature increases to +infinity, which is halfway up the thermometer. Temperature=infinity is synonymous with temperature=-infinity; both of them correspond to β=0. As we continue to add energy, the temperature increases from -infinity through the range of negative values up to some small negative value at the top of the thermometer.
At some point we need to ask what “hot” means. You might very reasonably think that T=∞ would be hot, indeed infinitely hot. That’s true, but it is also true that T=∞ is only halfway up the temperature scale in figure 5. So we might say that negative temperatures are “hotter than hot”.
It’s fun to use expressions such as “hotter than hot”, but after the fun wears off we are left with ambiguities. It’s not clear whether “hot” should designate high temperature (the middle of the scale) or high energy and strong negative polarization (the top of the scale). So I will duck the question. I hereby define the term toasty to refer to the top of the scale, where there is high energy and strong negative polarization. Meanwhile, the term high temperature unambiguously refers to the middle of the scale.
As far as I know, the all-time record for the toastiest temperature in the universe is a fraction of a negative microkelvin. This was created by chemical means, using the H↑ + H↓ reaction to purify a sample of H↑ (spin-polarized hydrogen).
So, we can say that a very high temperature (say, one million degrees) isn’t very toasty. I’ve seen things much, much toastier than that.
You can measure the polarization by counting the number of up-spins minus the number of down-spins. This is often converted to a percentage by dividing by the total number of spins, giving a relative polarization that ranges from P=+100% to P=−100%.
The total energy is proportional to the total number of spins N, their polarization P, their magnetic moment µ, and the magnetic field B acting on them:
| E = N P µ B (1) |
When β=0, the spins are completely unpolarized. This is shown at the halfway position in figure 5. In the vicinity of β=0 (i.e. temperatures near ±∞), the polarization is small and is proportional to β. That is, if you cut the temperature in half, you get twice the polarization (when the polarization is small).
At all negative temperatures, there is a population inversion. That is, there are more spins in the high-energy microstate than in the low-energy microstate.
One must be careful in interpreting figure 5. At the coldest temperature, the system is in a single, definite microstate, namely the microstate with 100% polarization. Similarly at the top (toasty) end of the scale, the system is in a single, definite microstate, namely the microstate with −100% polarization. However, at mid-scale (high temperatures) the system is not (really, really not) in a single microstate, even though only a single P=0 microstate is depicted on the middle row of the figure.
There are actually two ways in which multiple microstates are associated with the middle row of the figure. For starters, every possible permutation of the “up” and “down” arrows counts as a different microstate (with the same polarization). For the β=0 row, there are many, many permutations, roughly √2N of them. In contrast, for the fully-polarized states at the coldest temperatures and the toastiest temperatures, there is nothing to permute, so what you see is what you get: just the one microstate.
But wait, there’s more. The high-temperature macrostate has zero macroscopic polarization, but that does not mean that it is built entirely of zero-polarization microstates. You can equally well achieve zero macroscopic polarization by a balanced combination of microstates with positive and negative polarizations. And in fact that’s what happens: In the T=∞ macrostate, all microstates (all 2N of them) are equally likely. This is represented by the braces that appear between the β numbers and the spin-up/down arrows in figure 5.
The entropy is a non-monotone function of temperature. In figure 5, you can see that entropy is small at the bottom of the thermometer (slightly positive temperature), then reaches a maximum at the middle of the thermometer (infinite temperature) and then returns to small values at the top of the thermometer (slightly negative temperature).
It is perfectly possible to have thermal equilibrium at negative temperatures. One spin system will be in equilibrium with another if and only if they are each internally in equilibrium and their temperatures are equal.
The story that explains equilibrium at negative temperatures is word-for-word the same as at positive temperatures.
The canonical example goes like this:
Two regions, A and B, start out as shown in figure 6. That is, A starts with seven spins, six of which are in the "up" microstate. Meanwhile, B starts with seven spins, four of which are in the up microstate.
The spins are all identical. The up microstate differs in energy from the down microstate.
If A and B are isolated, there are seven possible permutations of A and 35 possible permutations of B, for a total of 245. The entropy is therefore
| (2) |
(We consider only permutations, because those are the only microstates consistent with the constant-energy macrostate. Permutations occur by spin/spin coupling within the system.)
Now, we let A and B exchange energy with each other (while they remain isolated from other regions).
We now need to consider states such as those shown in the bottom of figure 6 ... that is, five up spins in each region. There are 21 permutations of A and 21 permutations for B, for a total of 441. So the entropy is
| (3) |
This configuration is more likely, by a factor of 1.7 or so. That’s because there are more ways it could happen. The entropy is larger by more than 3/4ths of a bit.
Note that the discussion in this section is completely independent of whether the spin-up state or the spin-down state has the lower energy! So the story is equally true for the positive-temperature case and the mirror-image negative-temperature case.
For a system with 1023 spins, the max-entropy macrostate is overwhelmingly more likely than others.
Feynman said the equilibrium is when all the fast things have happened but the slow things have not.
In the language of NMR:
It is within the realm of reasonable choices to declare t2 to be a fast thing and t1 to be a slow thing. Therefore paragraph (2) does not invalidate paragraph (1). It is not hard to find real systems where t2 is much less than t1
None of the preceding discussion in this section is restricted to two-state systems. However:
A so-called two-state system1 will always have a temperature. The only thing that matters is the population of the up state versus the population of the down state – and you can always curve-fit an exponential to two points.
For the corresponding thing with three states, in some cases it is possible to create states for which the concept of temperature is undefinable. That’s because you can’t curve-fit an exponential to three points if they’re not monotone. An illustration can be found in reference 1.