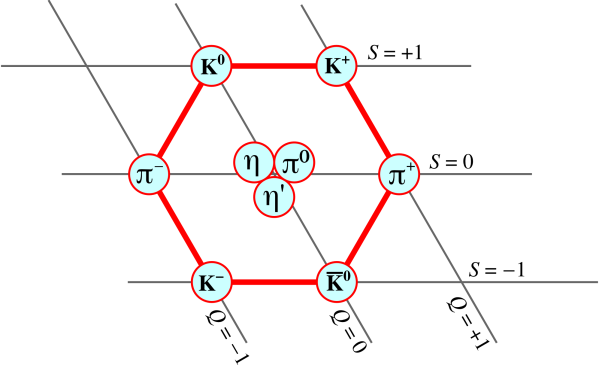
Figure 1: A Nonet of Lightweight Pseudoscalar Mesons
Let’s try to understand how quarks combine to form mesons.
For starters, let’s restrict attention to the three “light” quarks: up, down, and strange. These are an order of magnitude less massive than the other quarks, so this is a reasonable dichotomy.
Mesons are by definition composed of a quark and an antiquark. Obviously there are nine such mesons: there are three ways of picking the quark, and three ways of picking the antiquark.
So, the question arises: Why have people been talking for 50 years about the “eightfold” way whereby “eight” mesons form an “octet”????
Let’s be clear: There are nine mesons in this category, as shown in figure 1 and equation 1.
| (1) |
Sure, the η′ is heavier than the others ... but the η / η′ splitting is not larger than the η / π0 splitting.
In figure 1, Q represents electric charge, and S represents strangeness. For the each of the six mesons on the red hexagon, its antiparticle is diagonally opposite. For each of the three particles in the center, each one is its own antiparticle.
To make sense of this, let’s back up yet another step, so we can make contact with something you already know. This upholds the pedagogical principle: Learning proceeds from the known to the unknown.
Let’s consider the hydrogen atom. One proton and one electron. For purposes involving ordinary chemical reactions, all hydrogen atoms are alike, and magnetic fields are irrelevant. There is no magnetic field on earth that can affect the rate of a chemical reaction at ordinary temperatures. If you lower the temperature by four or five orders of magnitude, the story is completely different, and much more interesting. You can /stop/ the chemical reaction using a magnetic field. Been there, done that.
However, let’s forget about chemistry. Each hydrogen atom has four spin states: (electron up or down) ×(proton up or down). This contributes R log 4 to the molar entropy of a sample of hydrogen. These four states form a Hilbert space.
We can split this space in various ways. If we apply a strong external magnetic field, it splits “mainly” according to electron magnetic moment. There are two “main” states (electron up or down), each of which is slightly perturbed by the nuclear spin (proton up or down). This is the 2×2 representation.
On the other hand ... Suppose the external applied field is very weak compared to the internal hyperfine field. Then the atom is split “mainly” into two hyperfine states, triplet and singlet. The triplet is slightly split by the applied external field. This is the 3+1 representation.
Let’s be clear: You can convert 2×2 to/from 3+1 any time you choose. There is no God-given stone tablet that says one or the other is more fundamental. Your choice might depend on what sort of field is doing the splitting ... but if the two fields are comparable you might wind up using both representations, or neither. And from the chemist’s point of view, the splittings are irrelevant anyway; it’s all just hydrogen.
Returning to the quarks and mesons: There are nine mesons. Choosing one of three quarks and one of three antiquarks is the 3×3 representation. So far so good. Meanwhile, there is a way of splitting things that gives an 8+1 representation, namely an octet plus a singlet. So talking about “the” octet is weird, but not quite as crazy as it might have seemed at first.
The η′ meson is the odd man out, the singlet.
It must be emphasized that there is no God-given stone tablet that requires you to use the 8+1 representation. It is perfectly reasonable to lump them all together. They’re all just mesons. Nine mesons.
Note: The analogy here is imperfect. In the hyperfine situation, the singlet has a minus sign, and has the lower energy ... whereas in the meson situation, the singlet has nothing but plus signs, and has a higher energy. I will not attempt to explain this.
Let’s talk about the quark content of our nine mesons. For the six mesons on the red hexagon in figure 1, things are pretty simple:
| (2) |
To understand the other three particles, again we invoke an analogy. Consider a two-state system, such as the hydrogen molecular ion, or the ammonia molecule, as discussed in reference 1. Given two degenerate basis states |I⟩ and |II⟩, sometimes the states we are most likely to see in nature are the gerade and ungerade combinations, (|I⟩ + |I⟩)/√2 and (|I⟩ − |I⟩)√2. If the basis states are not degenerate, we still see linear combinations, but the mixing angle be more complicated; it won’t be simply 45∘.
So it is with mesons. We start with three simple basis states: uu–, dd−, and ss–.
The neutral pion is approximately the ungerade combination (uu– − dd−)/√2. The gerade combination is something we don’t commonly see. I call it a horton, denoted h.
The horton mixes with the third basis state, i.e. the ss– state. The two combinations give us the η and η′ states, as shown in the last two lines of equation 3. See also reference 2.
| (3) |
To summarize: Starting from the original three quarks and three antiquarks, we can form 9 basis states in the obvious 3×3 representation. We can understand the observed mesons, the 9 lightweight mesons, by taking linear combinations of these basis states.