Figure 1: Sailing Directly Upwind
We shall explain why the physics of sailing directly upwind is the same as the physics of sailing directly downwind, faster than the wind.
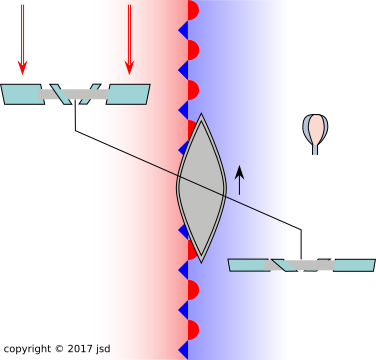
Imagine a sailing craft at the boundary between two fluid masses, as shown in figure 1. Such a situation could arise in various ways, as discussed in section 5.
Our craft has a propeller immersed in the blue fluid. The propeller has a relatively fine pitch. To a zeroth approximation, it serves to lock the craft to the blue fluid. The craft also has a turbine immersed in the red fluid. The turbine has a relatively coarse pitch, which means the fluid can flow through it relatively easily.
Figure 1 analyzes the situation using a reference frame comoving with the blue fluid. This is symbolized by the balloon, which is at rest with respect to the blue fluid. In this frame, we can understand that the turbine is turning, because of all the fluid flowing through it. It doesn’t turn very fast, because of the coarse pitch, but it turns at a decent steady rate.
The turbine drives the propeller. The coarse pitch of the turbine gives it mechanical advantage, so it overpowers the propeller, not the other way around. So the propeller turns a little bit, driving the craft forward a little bit relative to the blue fluid, as indicated by the black arrow.
In the chosen frame, the blue fluid doesn’t count as wind at all; it is just a bunch of stationary fluid. The only thing that counts as wind is the red fluid, and the craft is moving directly upwind against this wind.
Next, let’s analyze the exact same physics using a different reference frame. In accordance with Galileo’s principle of relativity, the observable behavior will be exactly the same ... just described in different words.
This time we choose a reference frame comoving with the red fluid, as symbolized by the balloon in figure 2. Once again, the propeller is immersed in the blue fluid, and to a zeroth approximation serves to lock the craft to the blue fluid.
In our reference frame, the red fluid does not count as wind; it is just a stationary mass of fluid. The blue fluid is the only thing that counts as wind. So to a zeroth approximation, the craft is just drifting downwind.
However, as it drifts, a great deal of fluid is flowing through the turbine. This drives the turbine a little bit, which in turn drives the propeller a little bit, so the craft moves downwind slightly faster than the wind.
Figure 3 shows another way of picturing the situation. The red gear and the blue gear are both locked to a common axle, so they rotate together. The pair is called the gig. The red gear engages the red rack, while the blue gear engages the blue rack.
We start by considering the case where the red gear has radius r1 = 0. When the gig rotates through an angle θ, it advances relative to the red rack by a distance r1 θ, which is zero. In other words, the gig is locked to the red rack. If we imagine the red rack to be the air mass, this corresponds to a sailing craft with a huge spinnaker, carried along with the wind.
The blue rack is moving to the left relative to the red rack and relative to the gig. So the gig will be rotating. The gig can use this rotation to drive an electrical generator. It can harvest energy from the relative motion, even while it is being carried along with the wind.
You may object that trying to drive a generator will cause the gig to make some leeway, i.e. to travel downwind more slowly than it otherwise would, to some extent. That’s true, but that’s an engineering issue, not a fundamental physics issue. This section emphasizes gears (rather than wind and water) to drive home the point that the amount of leeway can be made negligible, under a wide range of conditions.
We now turn to the case where the red gear is nonzero, but still small compared to the blue gear. That is, r1 ≪ r2. When the gig rotates, it advances to the right relative to the red rack by an amount r1 θ, and relative to the blue rack by an amount r2 θ.
Let’s be clear: Relative to the blue rack, the red rack is moving rightward, and the gig is moving rightward faster than that. This corresponds to sailing directly downwind faster than the wind.
At the next level of detail, note that the racks move relative to each other by an amount x = (r2 − r1) θ. We can rearrange this to obtain an expression for the amount of rotation:
| (1) |
So, relative to the blue rack, the gig moves by a distance
where the first term on the RHS of equation 2a arises because the red rack is moving, and the second term arises because the gig is moving faster than that.
For most people, it is easier to imagine ideal (or almost-ideal) gears than it is to imagine ideal sails or propellers, which is the attraction of figure 3. Even so, there are limits: If you get greedy and try to make r1 equal r2, you won’t get infinite downwind speed; instead you will just break the teeth off the gears. To say the same thing another way: When r1 equals r2, the two racks are locked to each other; if you try to move one relative to the other, something will break.
Once upon a time, I posed the sailing upwind/downwind question as a riddle, over lunch, at work.
The next day, a coworker called me and asked me to come down to his office.
−− I want to show you the answer to your question.
++ Why don’t you just tell me over the phone.
−− No, I want to show you the answer.
++ OK, whatever.
When I got to his office, it all became clear. He had built a working model, with a turbine and gears to drive the wheels. He blew on it with a powerful hair dryer, and it obediently crawled upwind.
The situation we have been discussing could arise in various ways:
Mechanical advantage is critical here. Without it, the turbine would not turn the right way, and upwind sailing would not be possible. See also reference 1.
The same concept is critical to understanding how a jet engine, and in particular why it rotates the right way, as discussed in reference 2.
One part of this story is particularly simple: If you can sail directly upwind, you can sail directly downwind faster than the wind. And vice versa. Galileo’s principle of relativity guarantees it.