|
| |
| Figure 1: Light Pulses in the Frame of the Transmitter | Figure 2: Misrepresentation of Light Pulses | |
This document is a companion to reference 1. There are quite a few things that I didn’t want to talk about in that document. Indeed I don’t really want to talk about them at all. However, I feel obliged to mention them, if only so that you will know that de-emphasizing them is fully intentional.
If you were surprised the first time you saw the spacetime approach, you are in good company. Einstein himself was so invested in the old way of doing things that initially he could not make sense of what Minkowski had done. On the other hand, before long he hopped on the bandwagon, and based all the rest of his work (including general relativity) on the spacetime approach.
At one level, some of this comes down to a choice of terminology:
| Some folks choose to include gamma factors in their definition of “the” mass, “the” time, et cetera. To a first approximation, it is pointless to argue that their choice is wrong; it’s just a choice. | Some folks find it elegant and convenient to choose the spacetime approach, but that’s still just a choice, not a law of nature. |
At another level, these choices have real consequences, because they color our thinking. They don’t fully control our thinking, but they do color it.
In general, there is a continuum: Some choices are purely matters of taste, and can be made freely and arbitrarily. Sometimes there are strong reasons for preferring one choice to another in this-or-that situation. Finally, sometimes there are questions of right and wrong.
Specifically: The archaic (pre-1908) approach can be made to work, especially for simple special-relativity problems. On the other hand, it will have to be unlearned before there can be any modern understanding of the topic ... or any extension to more advanced topics, including general relativity.
I am quite pleased that reference 1 does not even mention time dilation, FitzGerald-Lorentz contraction, or velocity-dependent mass (section 2.1). It does not mention poles in barns. It does not mention observers (section 2.2). It does not mention axes (section 2.3).
| Special relativity is not paradoxical, if you think about it the right way. Special relativity is the geometry and trigonometry of spacetime ... nothing more and nothing less. A great deal of what you know about three dimensions can be applied directly four dimensions, and a even more can be applied with minor modifications. | In some quarters, it is fashionable to make special relativity seem as weird and paradoxical as possible. This is spectacularly unwise. |
| More generally: The laws of physics – when correctly stated – do not contain any paradoxes, so far as we know. | You can cook up all sorts of paradoxes by mis-stating the laws of physics. This applies to basic mechanics, relativity, and every other branch of physics. |
| We do not introduce the subject of mechanics by talking about mechanical paradoxes. We do not introduce the subject of thermodynamics by studying the details of perpetual motion machines or other impossible and/or paradoxical devices. | I mention this because it is easy to make special relativity (or anything else) look weird. All you have to do is mis-state things. |
| For more than 100 years, it has been the consensus of informed opinion that a change in the x-component of velocity corresponds to a rotation in the tx plane. Rotations cannot change the length, if you define length properly. Ditto for elapsed time. Ditto for the mass. | There was a time, more than 100 years ago, when people did not understand rotations involving the 4th dimension. As a result, they had some very strange notions about time and length. They thought that the “length”, “elapsed time”, and “mass” would depend on what reference frame was used. |
| Let’s be clear: If you have never heard of Lorentz contracted rulers, time-dilated clocks, and velocity-dependent mass, that’s good. Keep it that way. Every minute you spend learning about that is at least two minutes wasted, because you will have to unlearn it if you want to really understand special relativity, let alone general relativity. |
| For a discussion of the history and pedagogy of the so-called “relativistic mass”, see reference 2. |
| There is energy, and part of the energy is rest energy, and the rest energy is proportional to mass (assuming m≠0). There is only one kind of mass, and it is a Lorentz scalar. It is the same in all frames. It is independent of velocity. | Under no circumstances does it make sense to talk about «rest mass». I mention this because there was a time when people considered the hypothesis that mass might be frame-dependent, i.e. velocity-dependent. This never worked; different ways of calculating the mass gave different answers, leading to “longitudinal mass” and “transverse mass” and who-knows-what else. Don’t go there. |
| In high school algebra, when you learned about rectangular coordinate systems and polar coordinate systems, you did not need to anthropomorphize them. That is, you did not need to imagine an “observer” attached to the rectangular frame and another “observer” attached to the polar frame. | I mention this because in some quarters, it is fashionable to emphasize the role of the “observer” in special relativity. This is a Bad Idea. |
| In particular, when we measure the 4-velocity of a particle at rest in the red reference frame, we get u = [1, 0, 0, 0]@R, which is not zero. This is important, because it the linchpin of the consistency discussed in reference 1. | In contrast, if we were to measure the 4-velocity relative to an actual observer we would get zero, because the observer himself has a nonzero 4-velocity. It is mathematically true that the 4-velocity relative to the observer is zero, but this is unhelpful, because it is the answer to the wrong question. |
| Both the observer and the particle are moving toward the future at the rate of 60 minutes per hour. We measure positions, velocities, et cetera relative to the coordinate system ... which is not moving. | It is a Bad Idea to measure things relative to the observer himself. |
| Any given contour of constant t – by definition – does not move in the t direction. | Any real object necessarily has a nonzero t-component to its 4-velocity. That is to say, any real observer (or any other real object) necessarily crosses contours of constant t as it flows along its world line, flowing through spacetime. |
| Therefore we must consider the contours of constant t to be artificial. They are mathematical abstractions, not real things. | The so-called observer is presumably real, with a nonzero 4-velocity. |
| This is important, because the physics is simple when expressed in terms of the coordinates, expressed relative to the non-moving, abstract coordinate system. | The physics would be disastrously complicated if expressed relative to the motion of any real observer. |
| In each coordinate system, it is important to keep track of the contours of constant t, contours of constant x, constant y, and constant z. | Talking about axes is asking for trouble. The so-called x axis is a contour of constant y, constant z, and constant t. The so-called t axis is emphatically not a contour of constant t. Loosely speaking it is a contour of “everything except” t. Specifically, it is simultaneously a contour of constant x, constant y, and constant z. |
| The contour of constant t is a 3-dimensional hyperplane extending in the x, y, and z directions. | The t axis is a one-dimensional line extending in the t direction. |
| If you know where the contours of constant x are, you can easily find the x-projection of any vector just by counting contours. | You may have been taught to find the x-component by “projecting” the vector onto the x axis, but this is tricky to do, since it requires an orthogonal projection. Unless the contours have been carefully marked out, it may not be obvious what the relevant orthogonal direction is. Conversely, if the contours have been marked out, you don’t need the axis at all. For details, see reference 3. |
| Many people contributed to the development of relativity. The fundamental principle of relativity was clearly enunciated by Galileo in 1632; see the quote in reference 1. Our understanding of relativity at high speeds includes contributions from Michelson, FitzGerald, Lorentz, Poincaré, Einstein, Minkowski, and many others. | I mention this because there are lots of references out there that insist that Einstein invented the principle of relativity, that Einstein invented the idea that the speed of light is the same in all reference frames, that Einstein invented the idea that time is the fourth dimension, et cetera. He didn’t. |
| I have nothing against Einstein. He was a smart guy. He contributed a lot. I’m happy that he won the Nobel prize. I also consider it fitting that his prize was not awarded on the basis of special relativity. |
| As of 1901, Poincaré and Lorentz knew more about relativity than Galileo ever did. As of 1905, Einstein knew more about relativity than Poincaré and Lorentz did. As of 1908, Minkowski knew more about relativity than Einstein did. This is how science works. Newton said he stood on the shoulders of giants. |
| There is no law that says pedagogy must recapitulate phylogeny. That is, just because Einstein approached the subject in such-and-such way in 1905 does not mean we have to approach it in the same way. | In some quarters it is fashionable to pretend that the development of relativity began and ended in 1905. This is insane. |
| Again: Special relativity is the geometry and trigonometry of spacetime. As such, it affects everything: fast-moving particles, slow-moving particles, and everything else. | There was a time, more than 100 years ago, when special relativity was focused on electromagnetism. The title of Einstein’s 1905 paper was “On the Electrodynamics of Moving Bodies”. |
| Of course, special relativity has some interesting things to say about light. | The relativity of electrodynamics is not even the tip of the iceberg. |
| Electromagnetism played an interesting role in the development of special relativity, but that is ancient history now. | Special relativity is not limited to electromagnetism, in the same way that genetics is not limited to peas and fruit flies. |
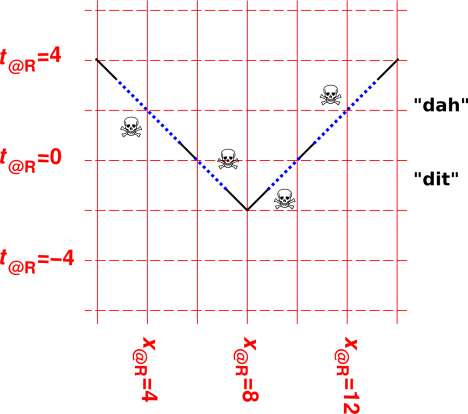
The story behind figure 2 goes something like this:
In this list, item 3 is totally wrong, and item 2 is partly wrong, in the following sense:
| Obviously the light “moves” past a benchmark that is stationary in some chosen frame. | You can’t analyze this from the light’s point of view, because there is no reference frame comoving with the light. a 45∘ diagonal line in spacetime spans zero proper time from end to end, so there is no time for anything to happen. |
| For spaceships it is usually a good strategy to analyze things using the ship’s proper time, using frames comoving with the ship. This is the natural choice. | When analyzing light pulses, there is no natural frame of reference. You have to pick something. |
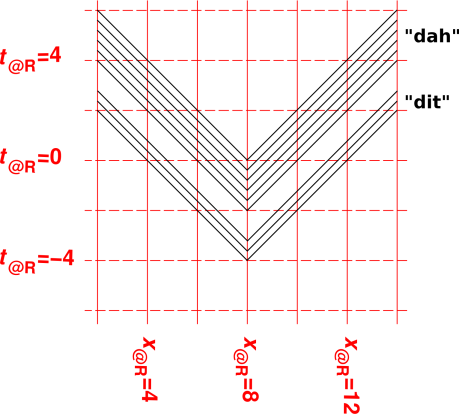
Another way you can tell that figure 2 is wrong is that the entire pulse is emitted in zero time in the red reference frame. It is emitted at (t,x) = (−2,8) in the red frame. Contrast this with the pulse in figure 1, which is emitted over an extended period of time, from t=−4 to t=0 in the red frame.
The correct procedure is to give each feature of the electromagnetic wave its own worldline. The feature could be a peak, trough, node node, or whatever. The feature does not evolve from one end to the other of the worldline. In figure 1 you can measure the period of the wave by measuring vertically, i.e. in the dt@red direction. Similarly you can measure the wavelength by measuring horizontally, i.e. in the dx@red direction. Such things cannot possibly be measured in the 45∘ direction, i.e. in the direction of propagation.
For any object with nonzero mass, such as a railroad train, muon, or whatever, you can talk about what happens in the rest frame of the object (assuming the whole object is moving with a uniform velocity). You cannot do anything comparable with a photon. There cannot possibly be any reference frame comoving with the photon.
Note that gamma [aka cosh(ρ)] appears in two places on the diagonal of the Lorentz transformation, equation 1 Possibly the #1 most common mistake that non-experts make is to get hypnotized by the diagonal elements to the neglect of the off-diagonal elements, namely beta·gamma [aka sinh(ρ)]. In [t,x] space this has to do with the breakdown of simultaneity at a distance. In [E,pxyz] space it means something else, and in [electricity, magnetism] space it means something else yet again.
| (1) |
When explaining relativity, the off-diagonal terms have to be a big part of the story.
I guess this is yet another reason why I don’t like terminology where gamma factors are built into the definitions of “the” mass et cetera. That puts too much emphasis on the gamma factors relative to the the beta·gamma factors.
Also, whenever you see somebody wrapped around the axle of a fallacy this is one of the first things you should check for ... no matter what terminology they are using.
Once upon a time I saw1 the following equation in a textbook. It was supposed to be a “fundamental” equation.
| (2) |
It turns out that equation 2 is messy, inelegant, incomplete, and inconvenient. In contrast, we get more convenience and more insight from the definition of momentum, as defined in e.g. reference 1, namely:
| (3) |
Ask yourself, which would you rather remember, equation 2 or equation 3? Pedagogical tactics are somewhat a matter of taste, but here are my recommendations:
As a general rule, if you see a relativity formula involving lots of square roots and three-dimensional vectors, you should look around for the corresponding spacetime formula. The point is, the spacetime approach will almost certainly be simpler, more elegant, more powerful, and in every way better.
Here’s another example that serves to make the same point: Once upon a time, I saw the following equation in a textbook. It was advertised as the relativistic “position update” formula. That is, if we know the momentum, it tells us how the position changes during a small amount of elapsed time.
| (4) |
Compare that to the fully four-dimensional spacetime equation:
| (5) |
Equation 5 is a clear expression of a simple concept. It is vastly clearer than equation 4. It is also 33% more powerful, because it gives us all four spacetime components, not just the three spacelike components. It is the nice, simple, modern (post-1908) way to represent the physics. It is obviously correct, as a corollary of the definition of velocity, namely:
| (6) |
Equation 4 is not wrong, it’s just ugly and messy. This is the penalty you pay for thinking in pre-1908 three-dimensional terms.
Again: As a matter of tactics, in my opinion, equation 5 is the equation we want to remember. It should be the starting point for any analysis. With any luck, we won’t need equation 4, because there is a lot we can do with equation 5 directly. In other cases, we can always complexify the equation to the extent necessary. The following calculation is carried out in reference 1:
| We start with equation 5. | We understand this equation. |
| If we want to calculate in terms of the lab-frame time Δt rather than the proper time Δτ, we can do that, but we will need to stick in a factor of γ, i.e. a factor of dt/dτ. | We understand what this factor means and where it comes from. |
| Then if we want to express γ in terms of the momentum, we can use trig identities to do that. | We understand that trig identities are just trig identities. |
The result at this point will resemble equation 4. Approaching it this way lets us understand what’s going on. In contrast, if we had started with equation 4, it would have been much harder to remember, and much harder to understand.
| It is 100% OK for experts to discuss misconceptions amongst themselves. | With rare but sometimes important exceptions, it is not a good idea to discuss misconceptions in front of students, especially in the introductory course. |
Mentioning a misconception in front of naïve students is at least as likely to reinforce the misconception as to dispel it. For more on this, see reference 4.
In almost all cases, the best strategy is to get the right idea out there first. The misconception can be discussed later, after the students have a firm foundation of correct ideas that can be used to deal with the misconception.
To say the same thing another way, if you find yourself arguing against misconceptions, it usually means the previous instruction wasn’t handled properly.
For example, consider the contrast:
| You hope students do everything correctly the first time, using something like figure 1 and the associated figures that appear in reference 1. | Figure 2 represents some seriously incorrect physics. You hope students never fall into this trap. |
Whatever the cause, sometimes students do fall prey to misconceptions. You need to have arguments that you keep in reserve, arguments that you can trot out if/when the need arises, to combat this-or-that misconception.