1  Statement of the Puzzle

Consider the circuit diagrammed in figure 1. There are six resistors. Five of them are identical, but the sixth one is different. Assume the difference is large enough to be readily measurable with an ordinary ohmmeter.

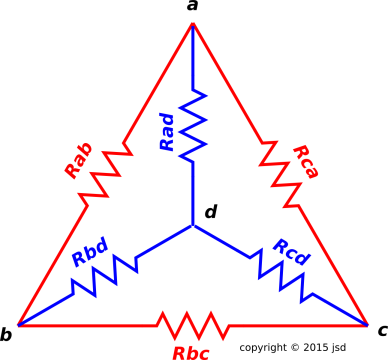Figure 1: Tetrahedral Resistor Network, Circuit Diagram

Here’s a puzzle for you: Figure out which of the resistors is the oddball, by measuring the circuit using an ohmmeter. You must measure the circuit as it is, without disassembling it.

Additionally, try to figure it out using the smallest number of measurements. Also try to figure out the actual resistance of each of the elments.

Note: You can make the problem dramatically easier by assuming that the odd resistor always has less resistance than the others, perhaps by building a completely symmetrical network and then adding something in parallel to one of the elements. At this point the only nontrivial bit is to figure out the value of R without doing a ton of work, which requires a little bit of insight.

However, today we will solve the hard version of the problem, allowing the odd resistor to be larger or smaller than the others.

2  Discussion

1.

We note that the circuit has the symmetry of a tetrahedron. If all the resistors were the same it would be a regular tetrahedron, but since one of the resistors is different it is a slightly irregular tetrahedron. The symmetry is discussed in more detail in item 13.

2.

Let the resistance of the normal resistors be r, and let the resistance of the oddball resistor be x.

3.

Notation: R_ab is the physical resistor connecting node a to node b. Meanwhile, Z_ab is the measured edge resistance when we apply the ohmmeter to nodes a and b. It includes contributions from the physical resistor plus all the stuff in parallel with it.

4.

Pick any resistor in the network, such as R_ab. Four of the other five resistors will be adjacent to this one, by which we mean they connect to it at one end or the other. The remaining resistor is located on the diametrically opposite edge of the tetrahedron. In this case that is R_cd.

5.

Terminology: The oddball resistor is sometimes called the odd pole of the tetrahedron. The resistor diametrically opposite the odd pole is the normal pole. The remaining four resistors are said to be on the equator, halfway between the two poles.

6.

Note that if R_cd is the oddball, all the others are normal, and by symmetry R_cd contributes nothing to the measured resistance Z_ab, and in fact you can easily show that

Znp   =   r/2     (normal pole)

(1)

independent of x. All you need for this are the basic formulas for resistors in parallel and resistors in series.

7.

It is equally true that if R_ab is the oddball, then the situation is once again symmetric, and R_cd contributes nothing to the measured resistance Z_ab. You can easily show that

Zop   =   x∥r     (odd pole)      (2a)   =   x r x+r          (2b)      x   =   r Zop r − Zop          (2c)

8.

There will be four observed resistances on the equator. By symmetry, these will all be equal. Qualitatively speaking, the result will necessarily be somewhere in between the two polar readings: the equatorial readings will not be as strongly affected by the oddball as the odd polar reading, but they won’t be completely immune like the normal polar reading.

Alas at this point the readings still don’t solve the problem, because x could be larger or smaller than r. Knowing that the equator is somewhere in between doesn’t tell us which pole is which.

9.

With some thought you can convince yourself that the equatorial reading is closer to the normal polar reading than it is to the odd polar reading. This is because the effect of the oddball is more diluted by the complicated series/parallel network.

You can check that this result is plausible by considering the extreme cases x=0 and x=∞. If you want reliability, not just plausibility, you have to do the math, as discussed in the next item.

10.

Calculating the exact value for the equatorial readings is a chore, but it can be done. It helps to apply the wye-delta transformation to the blue resistors in figure 1, to produce the equivalent circuit shown in figure 2.

Figure 2: After the Wye-Delta Transformation

In accordance with the usual formula, the resistances of the delta-circuit elements are known in terms of the original wye-circuit elements:

Qab   =   Rad Rbd + Rbd Rcd + Rcd Rad Rcd

(3)

And similarly for all cyclic permutations of (a,b,c).

What remains is a relatively simple series/parallel combination. We can take it step by step. First we combine each red resistor with the corresponding blue resistor:

Kab   :=   Rab ∥ Qab

(4)

Then we combine those in series/parallel:

Zab   =   Kab ∥ (Kbc + Kca)

(5)

The final observed impedance is:

Zeq   =   5 x r + 3 r2 8 x + 8 r     (equator)

(6)

11.

All the results are shown in figure 3. The abscissa is the arctangent of x, which allows us to scan from x=0 to x=∞ in a nice systematic way.

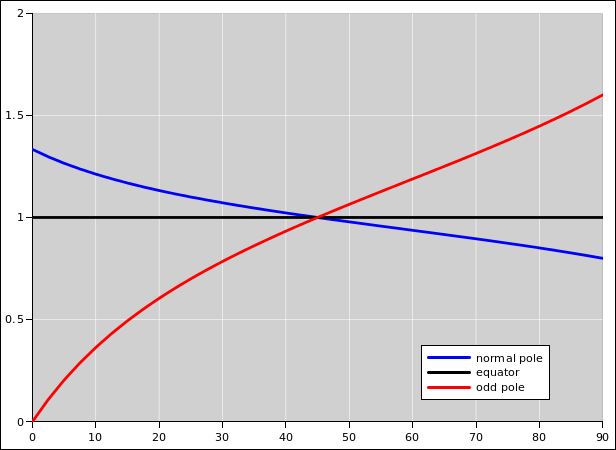Figure 3: Tetrahedral Resistor Network Readings

12.

The three formulas can be put into a common form as follows:

4 x r + 4 r2 8 x + 8 r         (normal pole)         5 x r + 3 r2 8 x + 8 r         (equator)             ‵ 8 x r + 0 r2 8 x + 8 r         (odd pole)

(7)

13.

Note the contrast:

Speaking of the physical resistors R: There are four normals on the equator plus one more on the normal pole, for a total of five normals. Finally there is the oddball on the opposite pole.

Speaking of the measured resistances Z: There is a group of four all the same, plus one higher, plus one lower.

Do not confuse the symmetry of the inputs with the symmetry of the outputs. That is, do not confuse the symmetry of the structure with the symmetry of the function.

3  Solution Procedure

3.1  Simple Version

This version requires four measurements in every case.

1. Pick three edges that form a triangle. Measure them. You are guaranteed that any such triangle will contain one polar edge and two equatorial edges.
2. You can identify the polar edge because it is different from the other two. Measure the diametrically opposite edge, since that is the other pole.
3. Whichever pole has a reading closer to the equatorial readings is the normal pole; the other one is the odd pole.
4. You can determine the value of r from equation 1. You can then determine the value of x from equation 2c.

3.2  Fancy Version

This version is optimized to use the minimum number of measurements. Usually four measurements are required, but if you’re lucky you can sometimes get by with three.

1. Pick any two adjacent edges and measure the resistances.
   • If they are the same, you have identified the equator. One pole will bridge the V formed by these two edges (closing the triangle), and the other pole will connect to the point of the V. Measure the two poles.
   • If the first two edges are not the same, select one of those edges and measure the edge that is diametrically opposite. You now have three measured edges that form a skew figure, not a triangle.
     • There is a 50/50 chance that all three are different, in which case the extreme values are the poles. This is the only case where you can get by with three measurements. All other cases require four.
     • If two are the same and one is different, the different one is a pole. Measure the opposite pole.
2. Whichever pole has a reading closer to the equatorial readings is the normal pole; the other one is the odd pole.
3. You can determine the value of r from equation 1. You can then determine the value of x from equation 2c.

4  References

1.

Donald Simanek,
“Challenging Physics Problems”
https://www.lhup.edu/~dsimanek/scenario/puzzles.htm