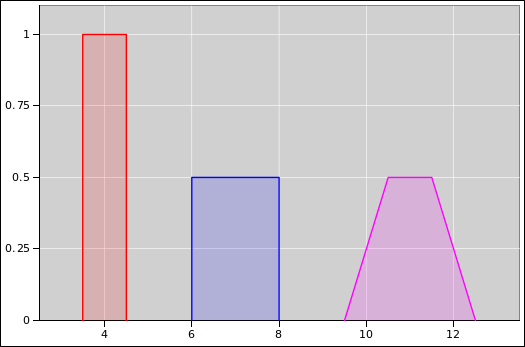
Figure 1: Trapezoid as the Convolution of Two Rectangles
This is relevant to calculating uncertainties. If you have two inputs that exhibit rectangular distributions, the output will exhibit a trapezoidal distribution.
Suppose we have a rectangular distribution R1 where the half-width and half-maximum (HWHM) is h1, and similarly R2 where the HWHM is h2. We assume for convenience, without loss of generality, that h2 ≥ h1.
We now calculate y := x1 + x2, where x1 is drawn from R1 and x2 is drawn from R2. This situation is shown in figure 1.
Here are some of the key relationships:
| R1 | R2 | Trapezoid | Lebesgue | Remarks | |||||||||||||||
| center: | c1 | c2 | c1 + c2 | ||||||||||||||||
| HWHM: | h1 | h2 | h2 | L∞ | independent of h1 | ||||||||||||||
| HWtop: | h1 | h2 | h2 − h1 | ||||||||||||||||
| HWbase: | h1 | h2 | h2 + h1 | L1 | worst-case deviation | ||||||||||||||
| stdev: | σ1 | σ2 | √(σ12 + σ22) | L2 | Euclidean norm | ||||||||||||||
| stdev: |
|
|
| ||||||||||||||||
| HWHM/stdev: |
|
|
| ||||||||||||||||
| height: |
|
|
| normalized to unit area |
The HWHM of the trapezoid is independent of the width of R1, so long as R1 is narrower than R2.
The ratio of HWHM to stdev varies quite a bit: