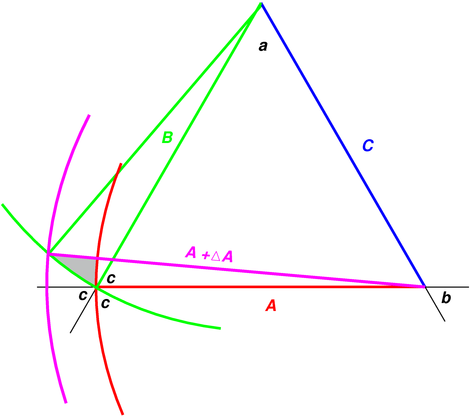
Figure 1: Triangular Truss
We wish to understand what happens when we slightly change the length of one side of a triangular truss, as shown in figure 1. The truss is made of three struts A, B, and C. The struts are held together by a pin at each vertex. The struts are free to rotate around the pins, so as to let the truss assume its natural triangular shape.
We start out with the triangle ABC, shown in red, green, and blue. The angle a is opposite side A, the angle b is opposite side B, and the angle c is opposite side C.
We consider what happens when we increase the length of one side from A (shown in red) to A+ΔA (shown in magenta). For simplicity, and without loss of generality, assume side C does not move. We want to figure to remain a closed figure, so we need to let the other two sides rotate. To find the location of the new vertex, we must find the intersection of the circle of constant radius A+ΔA (shown in magenta) with the circle of constant radius B (shown in green).
We now focus attention on the gray-shaded region. To first order in ΔA/A, we can approximate this region as a triangle, indeed as a right triangle. By using the “opposite angles are equal” theorem enough times, and the fact that a circular arc is (locally) perpendicular to its radius, you can ascertain that the downward-pointing vertex of the gray triangle is equal to c.
Then trigonometry tells us that
| = tan(c) (1) |
| = sin(c) (2) |
whence
| Δb = |
| (3) |
| Δa = |
| (4) |
And since a+b+c = const = 180∘, we have:
| Δc = − Δa − Δb (5) |
This concludes the main derivation.
As a check on our work, we can divide equation 2 by equation 1 to obtain:
| = −cos(c) (6) |
In the case of an equilateral triangle, this reduces to
| Δb = Δc = −½ Δa (7) |
which is as it should be. If you do not immediately see why this result must be correct, think about the symmetry. Consider what happens to the angles if you lengthen all three legs by the same amount.