Units of Measurement
John Denker
* Contents
1 Expressing Units, and Converting Units
-
As a first example, suppose the length of a certain
hallway is L. This length is a thing unto itself, a mathematical
thing, indeed a physical thing. It exists whether you measure it or
not, and it exists independently of whatever units – if any – you
decide to use. Therefore the length is not «L feet» or «L
yards» or anything like that; the length is simply L.
-
Now suppose we measure the hallway and find that it
is 10 yards long. We can write that as an equation:
Note the structure on the RHS: 10 is a pure number, while yd is a unit
of measurement. L is not equal to 10, and L is not equal to yd;
rather, L is equal to the product, 10·yd.
-
As a separate matter, we know:
|
1 yd | | = | | 3 ft | | (by definition)
|
| (2)
|
Therefore we can write:
Equation 3 comes from equation 2 by direct
application of the axioms of algebra, namely the definition of
division, and the definition of equality.
The axioms also say we can multiply the RHS of equation 1 by
unity. This gives us:
|
| |
L | | = | | 10 yd · (1)
| |
(4a)
|
|
| |
| | = | | 10 yd ·
| |
(4b)
|
|
which simplifies to
which is true and useful.
-
This whole discussion illustrates the real-world power
and generality of algebra. Units of measurement (such as ft and yd)
play by the same rules as algebraic variables (such as x and y).
- This is true even though ft and yd are known constants, so
technically speaking they’re not variables and they’re not
unknowns.
- Note that ft and yd are not numbers, and do not represent
numbers. They exist in an abstract space all their own ... 100%
abstract yet 100% practical.
-
This is the way smart people have been doing it for thousands of
years. In King Tut’s time, the royal cubit was equal to 7 palms, and
a palm was equal to 4 fingers. Nowadays kids learn in first grade
that a quarter is equal to 5 nickels, and a nickel is equal to 5
pennies; from this you can infer that a quarter is equal to 25
pennies.
The technique of writing equations to express the relationships
between units is used even in non-scientific settings such as
cooking; see e.g. reference 1. This is the smart way to do
it. (There are plenty of dumber ways, but let’s not get into that.)
The tactic of multiplying by unity is heavily used in science and
engineering at all levels, from high-school chemistry on up. It even
has a name: The Factor Label method.
In my experience, this is the #1 best response to those who claim
they have never had occasion to apply anything they learned about
algebra.
In simple cases, the Factor Label method can be carried out
mechanically, even by people who have no clue about algebra.
However, in more complicated cases – involving (say) square feet and
cubic yards – it helps to know the axioms of algebra. In all cases,
if you want to understand what’s going on, algebra helps a lot.
-
Some pretty smart mathematicians have looked into the
algebraic structure of units. In the metric system, a kilogram is
1000 grams. This was started by a committee that included de Borda,
Laplace, Monge, Condorcet, Legendre, and others. Later Gauss had a
few things to say about units.
-
On various odd occasions, it may be expedient
to strip the unit out of a quantity such as L. In such cases, the
algebraically reasonable way to write such things is L/yd and
L/ft ... with the units in the denominator. This leads to
the inelegant but correct equation:
This inelegant tactic is useful if you are using a calculator that
can multiply pure numbers but is too stupid to keep track of the
units. Such situations are becoming rare; any computer worthy of the
name can run a computer algebra system such as Macsyma that can
easily keep track of units, directly using equations such as
L=10yd.
In any case, it must be emphasized that the LHS of equation 6 is not «L feet», and the RHS is not «L
yards». The units belong in the denominator, because we
are stripping the units out of L by dividing them out.
It must also be emphasized that carrying around a pure number,
stripped of its units, is bad practice. You run the risk of
forgetting which units go with which number. Sometimes the penalty
for getting this wrong is on the order of three hundred million
dollars, as in the case of the Mars Climate Orbiter (reference 2 and reference 3).
 Figure 1
Figure 1: Mars Climate Orbiter mission logo
./img48logo-98t-s.png
-
As hinted in item 1, it is entirely possible
to measure something using no units at all. On more than a few
occasions I have been miles away from the nearest ruler, so I
recorded in my notebook that something was |——| long.
That’s an analog measurement.
2 Some Other Examples
There is a right way and a wrong way to express the units associated
with a given quantity.
2.1 Length and Area
Some simple yet useful examples include:
- The length L is 10 yards. L = 10 yd.
- The length L is 30 feet. L = 30 ft.
- The width W is 2 feet. W = 2 ft.
- The area A is 60 square feet. A = 60 ft2.
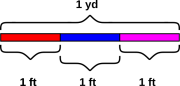
To a good approximation you can make a yardstick by gluing three
one-foot rulers together end-to-end, as shown in figure 2.
This gives us a concrete, physical basis for saying that 1 yard
“equals” three feet.
This physical interpretation is captured in the algebra, if we do
things right. For example, if we multiply two quantities together,
the numerical magnitudes get multiplied and the units get
multiplied. For example, if the length L is 30 feet and the width
W is 2 feet, the area A is given by:
|
A | | = | | L · W |
| | | = | | (30 ft) · (2 ft) |
| | | = | | 60 ft2
|
| (7)
|
It would be quite improper to say «the area was 60», or that
«the area was 60 feet». The area is 60 square feet.
2.2 Deprecated Example: C versus F
Here is an example of what not to do. This is taken from page 13
of reference 4.
|
☠ C | | = | | 5/9 (F − 32) | | ☠ |
| ☠ F | | = | | 9/5 C + 32 | | ☠
|
| (8)
|
|
In this document, we put equations and tables on a red background to
warn you about things that are not recommended. Similarly we
sometimes use «⋯» as scare-quotes around improper expressions.
This equation uses the unit of measurement (C or F) as a stand-in for
the thing being measured. This is a Bad Idea. It is diametrically
inconsistent with modern notions of unit-analysis.
There is a very important difference between the thing being measured
and the unit used to measure it, as discussed in
section 3.2.
2.3 Deprecated Example: Motor Data Plate
Here’s another example: Recently I was looking at the data plate on an
electric motor. It said:
| HP | : | | 1 | | Type | : | | C |
| RPM | : | | 1725 | | SF | : | | 1.0 |
| A | : | | 12.3 | | PH | : | | 1 |
| V | : | | 115 | | HZ | : | | 60 |
|
The colons on the data plate were meant to be interpreted as equal
signs.
If you find this confusing, good for you. This usage is considered
perverse, as indicated by the red background. This usage is exactly
backwards relative to how it should be done. However, you still see
it from time to time, so it is worth learning to recognize it. Here’s
how it should have been done:
| rated power | = | | 1 HP | | type | = | | capacitor-start |
| rotation rate | = | | 1725 RPM | | service factor | = | | 1.0 |
| max current | = | | 12.3 A | | arrangement | = | | 1 phase |
| voltage | = | | 115 V | | powerline frequency | = | | 60 Hz |
Table 2: Recommended Notation for Motor Data
If you are going to use the proper system you must strictly avoid
mixing it with the perverse system. This leaves us with the question,
what to do if you encounter something expressed the bad way, such as
the motor data plate mentioned above.
The simplest answer is to recognize that the RPM mentioned on the data
plate belongs on the RHS of the equation. Another option is to say
that the RPM belongs in the denominator on the LHS; this is inelegant
but not wrong:
| rated power / HP | = | | 1 | | Type | = | | capacitor-start |
| rotation rate / RPM | = | | 1725 | | service factor | = | | 1.0 |
| max current / A | = | | 12.3 | | arrangement / phase | = | | 1 |
| voltage / V | = | | 115 | | powerline frequency / Hz | = | | 60 |
Table 3: Another Good Notation for Motor Data
Note: Whenever you see the words “measured in” you can replace them
by “divided by”. This is a trustworthy rule for translating word
problems into equations. (It is analogous to the rule that says
in expressions like “one tenth of thirty” the “of” gets replaced
by “multiplied by”.)
2.4 Deprecated Example: Indicated Power of a Steam Engine
Here’s a trickier example of bad practice, from page 190 of
reference 4. For a steam engine:
I wish to make two different points about this. Please let’s
not confuse the two points.
- First, I call attention to the LHS, which is “indicated horsepower”.
This is another an example of using the unit of measurement as a
stand-in for the thing being measured. This is a Bad Idea, as
discussed in section 3.2.
The thing that is really interesting here is that the way units are
used on the LHS of equation 9 is inconsistent with the way
units are used on the RHS, and in particular with the way the
quantities P, L, A, and N are defined on the RHS of
equation 10.
This is relevant because if the people who use backwards units would
use them consistently backwards, we might chalk it up to a
difference of taste, not worth arguing about. But when they are
inconsistent about it, it’s more than a question of taste;
it’s an out-and-out blunder.
The best way to remove the inconsistency is to standardize on
the modern approach.
- Secondly, let us turn to the RHS. The book says:
|
average pressure | | = | | P pounds per square inch |
| stroke | | = | | L ft |
| area | | = | | A sq ft |
| there are | | | | N power strokes per minute
|
| (10)
|
|
which is interesting because in some sense those four statements are
dimensionally correct, if we consider P, L, A, and N to be “pure numbers”
(unitless and dimensionless) standing in front of explicit units.
This is, however, still not recommended. Even though it is not wrong
in any deep sense, it is not recommended. The problem is that the
numerical value of (say) A is tied to the units in use.
In contrast, modern practice is to do algebra using variables that
have not had units factored out, so that the area-variable expresses
the concept of area, no matter what units are used. For
example:
|
yes: | | A | | = | | (in whatever units) |
| yes: | | area | | = | | (in whatever units) |
| no: | | area | | = | |
| (11)
|
At this point you may be wondering about an interesting issue:
- Nowadays you can find software that will do algebra for
you. This includes keeping track of the units for you, including
conversions.
- Less-fancy computers, spreadsheets, and handheld calculators
calculate using pure numbers. This means you have to keep track
of the units separately.
So you could argue that a formula involving pure numbers has some value,
when you are using not-so-fancy electronic aids.
That is a valid argument, but there is a stronger counterargument.
The computer’s need for pure numbers can be accommodated within the
formalism of modern unit analysis. One could write:
|
indicated power/HP
= | | (P/psi) (L/ft) (A/ft2) (N/spm) |
|
| 33,000 |
|
(12) |
(where spm means power strokes per minute).
which has the advantage of being absolutely true no matter what units
the variables are measured in. If L is measured in (say) meters
instead of feet, then the problem is obvious: You will wind up with a
factor of (m/ft) left over. More importantly the solution is
obvious if you follow the factor-label method, because 1 (m/ft) is a
number with a well-known value.
3 Discussion
3.1 Units versus Dimensions
Units are not the same as dimensions. A foot and a yard have the same
dimensions, namely dimensions of length. But a foot and a yard are
very different units; one is smaller than the other by a factor of
three. Length and width have the same dimensions. Sometimes
length and width are measured in the same units, and sometimes in different
units. The distinction between units and dimensions comes into
sharp focus when we consider dimensionless units, as in
reference 5.
See reference 6 for an introduction to
dimensional analysis. All notions of units and dimensions rest on
deeper notions of scaling, as discussed in reference 7.
3.2 Units of Measurement versus Thing Being Measured
There is a profound difference between the unit of measurement and the
thing being measured. For example, if you are measuring a
piece of fabric with a yardstick, the fabric is not to be confused
with the yardstick. The fabric is the thing being measured, and the
yardstick embodies the unit of measurement.
Another example can be found in equation 8. Temperature is
the thing being measured; degrees C or degrees F are the units of
measurement.
Yet another example is the rotation rate in table 2.
The rate is the thing being measured, and RPM is the unit of
measurement. Just as the rulers in figure 2 have physical
significance, the RPM has physical significance. If the rate changes
from 1725 RPM to 1730 RPM, the RPM is not what changes; the rate is
what changes. It makes absolutely no sense to write RPM = 1725.
Writing such a thing is super-sloppy.
3.3 Dimensions Named After Units
Sometimes, the thing being measured is named after a unit. Examples
include
- voltage
- acreage
- yardage (football)
- wattage (lightbulb)
- footage (film)
- square footage (within a building)
- mileage (fuel economy)
- mileage (on the odometer of a used car)
- percentage
- tonnage
It must be emphasized that the physical quantity is not required
to be measured in the named units.
4 References
-
-
“Baking Conversion Table”
http://www.weekendbakery.com/cooking-conversions/ -
Douglas Isbell, Mary Hardin, Joan Underwood,
“MARS CLIMATE ORBITER TEAM FINDS LIKELY CAUSE OF LOSS”
http://mars.jpl.nasa.gov/msp98/news/mco990930.html -
“Mars Climate Orbiter Fact Sheet”
http://mars.jpl.nasa.gov/msp98/orbiter/fact.html -
Reno C. King Jr.,
Marine Engineering
Prentice-Hall (1948). -
John Denker,
“Dimensionless Units”
www.av8n.com/physics/dimensionless-units.htm -
John Denker
“Dimensional Analysis”
www.av8n.com/physics/dimensional-analysis.htm -
John Denker,
“Scaling Laws”
www.av8n.com/physics/scaling.htm