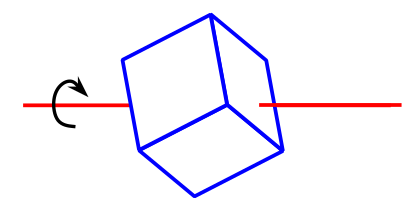
Figure 1: Skewered Cube
Here’s an elegant little riddle for you.
As illustrated in figure 1, suppose I take an ordinary uniform solid cube and skewer it with an axis that runs through an arbitrary point on one face, perhaps (x,y,z) = (0.5, 0.321, π/8), thence through the center of the cube, and out the opposite face. Question: what can you say about the moment of inertia of the cube as it rotates about this axis?
Hint #1: There is something very important you can say even without writing down the exact solution. This is the whole point of the question.
Hint #2: Given the results of hint #1, you should be able to write down the exact answer using nothing more than a pencil and a 3"x5" piece of paper. If you are tempted to use something more than that, you’ve missed the point.
Hint #3: The moment of inertia is really the tensor of inertia. It is a second-rank tensor.
Hint #4: What is a vector? Is it some arbitrary collection of 3 numbers? What about a tensor? Is it some arbitrary collection of 9 numbers? Or is it more special than that? Does it have some geometric and physical significance?
(The following hint is optional. If it helps you, fine; otherwise don’t worry about it.)
Hint #5: Why might somebody bring such a skewered cube to a class that is discussing the Wigner-Eckart theorem?