As an “induction hypothesis” we assume that we already have valid position and rate data for the old point N. Our tasks include advancing to the new point N+1, and printing out the results (not necessarily in that order).
- We evaluate the aerodynamics functions at point N. These functions take as input the positions and rates at point N, and produce as outputs the forces and accelerations. That is, we calculate the second derivatives as a function of the zeroth derivatives and the first derivatives.
- We should print out the results. This is the appropriate place to do so, because it is the first time we have full information about point N, namely the positions, rates, and forces. This is what should happen, but not what the current code actually does, as far as I can tell.
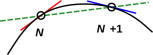
- We integrate to find the rate at point N+1, shown in blue in the figure, calculated from the rate at point N and the acceleration at point N.
- We integrate to find the position at point N+1. This is slightly tricky, because we could use the old rate (shown by the slope of the red line) and/or the new rate (shown by the slope of the blue line). In the example shown in figure 1, the old rate is an overestimate of the average rate, whereas the new rate is an underestimate of the average rate. The average rate is the average over the interval from point N to point N+1, as shown by slope of the dashed green line in the figure.
- We advance the time variable. This can be considered another example of integrating the equations of motion, according to the rule t = ∫dt. This may seem almost trivial, but we mustn’t forget to do it. Similarly we advance the point-counter from N to N+1, so that N+1 becomes the “current” point.
- At this point the current code prints out the results. This is somewhat problematic, because we don’t have force or acceleration data for the new current point (N+1). Those variables still have data from point N hanging around.
- We run the script, including any property-setting directives. In basic wind-tunnel mode, we assume the script sets all relevant positions and rates for point N. See item C for more on this.
- We calculate forces, moments, and accelerations for point N, by evaluating the aerodynamic functions, based on the current positions and rates.
- We print results to the output file.
- We advance the time variable (t). Similarly we advance the point-counter from N to N+1.
We would need to offer a choice of integration methods, just as the existing code does in non-wind-tunnel mode.
One disadvantage is that it is not an inertial frame. Doing physics in a non-inertial frame is tricky, but it can be done. In particular, the equations of motion contain must contain correction terms for the centrifugal field, for Coriolis effects, et cetera.
Another disadvantage is that, simply put, it is not the ECEF frame, i.e. it is not the natural frame for the wind tunnel user interface, as mentioned in item H.
However, everyone should beware that only the leading-order terms are implemented, and there are lots of other terms. Some of the unimplemented terms are not very small compared to the implemented terms.
For one thing, the familiar centrifugal and Coriolis terms only cover the case of steady rotation around a fixed axis. If the rotation rate is changing, or if the rotation axis is changing, all bets are off.
I reckon the existing code is good enough for ordinary aircraft and for ground vehicles, but a stated goal of the JSBSim project is to be able to handle spacecraft. I suspect that if you want to accurately model a spacecraft or a high-precision inertial navigation system, the equation of motion code would need major repairs.
I don’t want to make a big deal out of all this. I’m just saying that there is a price to be paid whenever you choose to use a non-inertial reference system.
One hypothesis is that the null integrator is supposed to represent a vehicle subjected to no forces, such as a freely floating space capsule. Alas, the "none" integrator, as implemented in the existing code, does not correctly represent this. It is implemented using zero lines of code, which means that it leaves out the centrifugal and Coriolis terms that the correct equation of motion must have (even in the absence of applied forces).
Another hypothesis is that the null integrator might leave the aircraft attitude frozen in some earth-fixed frame. This is wishful thinking; it is not what happens. In particular, if the aircraft attitude is changing (due to natural angular motion and/or due to being set by the script) then the aircraft’s momentum vector will magically change. That is, in the absence of forces, the vector’s projection onto the body axes will remain constant, but the actual physical momentum will change ... in violation of the most sacred basic laws of physics.
Remember that the momentum vector has physical and geometric reality, quite independent of its projection onto any set of axes. See reference 1 for details on this.
This also means that if you use a script to set the aircraft velocity and then set the attitude, you get a different result than if you did things in the other order, in violation of the commutativity objective expressed in item I.
You can optionally view non-commutativity as just an extreme version of the previous problem: Setting the attitude corresponds to a near-infinite rate of attitude change, and would require near-infinite correction terms in the equation of motion. The "none" integrator cannot handle any nonzero rate, let alone a near-infinite rate.
Also item F would require wind-tunnel mode to use non-null integrators.
To summarize: we have seen numerous reasons why wind-tunnel mode cannot be implemented simply by selecting the null integrator.