
|
Inner Diameter at bottom |
Inner Diameter at fill line |
Inner Height to fill line |
Volume to fill line |
||
| = | |||||
| in cm |
in3
quarts gallons |
cm3
liters |
|||
Here is the general formula, valid for any round container with uniformly sloping sides:
Volume = π/12 * (Bot2 + Bot*Top + Top2) * Hgt

If you are using nursery pots aka trade pots, beware that a so-called “trade gallon” is only about 0.7 real gallons. So a #7 nursery pot holds only about 5 real gallons. That's assuming you fill it to the normal fill line. (They would hold slightly more if you filled them to the brim, but that's immaterial and impractical.)
Sometimes it's even worse than that. I measured a #5 nursery pot that holds only 2.75 real gallons. Evidently sometimes a so-called “trade gallon” is only about 0.55 real gallons.
Here are some numerical examples. They work by filling in the variables in the online calculator:
The lesson here is that the “nominal” size of the pot doesn't reliably tell you the actual size. This is almost tolerable if you are doing your own over-the-counter shopping, since you can ignore the labels and buy something that “looks right”. On the other hand, if you are ordering stuff online, or if you tell a friend to buy a “five gallon pot”, then there can be significant misunderstandings.
When in doubt, you can measure the inside dimensions and plug into the formula above.
Various ways to measure the ID of the bottom of the pot include:
For best results, you need to measure both the top and bottom diameters, then use the fancy formula discussed above. That's because pots and buckets almost always have tapering sides, so they can be stacked for easy shipment and storage. On the other hand, in many situations it suffices to approximate the pot as a cylinder, using the average diameter. That is: split the difference between the top and bottom diameters, square that, multiply by the height, and multiply by π/4. This results in a slight underestimate, but it is accurate within a few percent in situations where the bottom diameter and top diameter are not wildly different. See below for details on this. To repeat, the exact formula for a cylinder is an approximate formula for a slightly-tapered pot:
Volume = π/4 * ID2 * Hgt (for a cylinder)
For a pot that is “almost” a cylinder, it doesn't much matter what we use as “the” ID, but for best results it makes sense to use some sort of average radius. So the question arises, what sort of average should we use? RMS? Arithmetic? Geometric????
As a warm-up exercise, let's consider a full cone. We know the volume of a cone is 1/3 of the volume of a cylinder with the same height and diameter. So the RMS average is not ideal, because that would predict 1/2 of the volume rather than 1/3. Meanwhile, the arithmetic average is not ideal either, because it would predict 1/4 of the volume (half of the diameter) instead of 1/3 of the volume. The geometric average is even worse, because it would predict 0 instead of 1/3. We want something that is somewhere between RMS and arithmetic.
Remarkably enough, all of the above form a family. We can interpolate between them. The general formula is:
Average = √[(Bot2+N*Bot*Top+Top2) / (2+N)]
for all N from 0 to ∞. In particular:
| N=0 | --> | RMS |
| N=1 | --> | conic |
| N=2 | --> | arithmetic |
| N=∞ | --> | geometric |
The relationships are shown in the following graph:
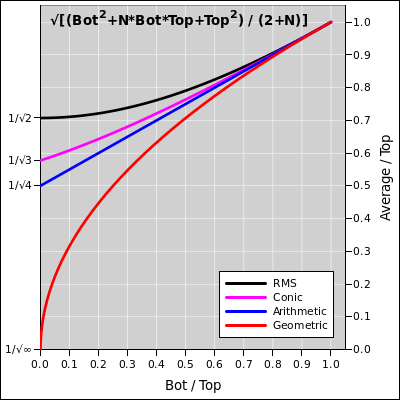
The N=1 average is in fact exactly correct for a truncated cone, as you can easily verify in lots of ways. (Grind out the integrals. Or just subtract one full cone from another.)