The streaklines displayed in the following animations are the result of an ideal experiment in which a passive tracer (like smoke) is injected in the flow, making the path of ``marked'' fluid particles visible. This allows us to follow, in a Lagrangian sense, the motion of the group of fluid particles that have passed through the same point. Since the flow is steady, the trajectories of such particles (the streaklines) are identical to the streamlines.

Changing periodically the color of all the smoke sources allows for a visualization of the time history of subsets of smoke particles injected in the same time interval. When the colored lines become shorter, the marked fluid particles are slowing down and vice versa.

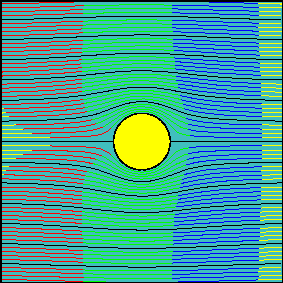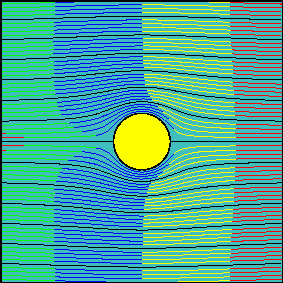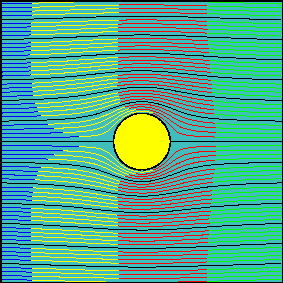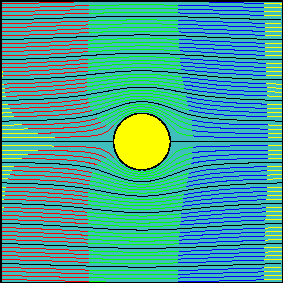
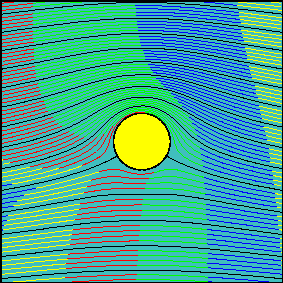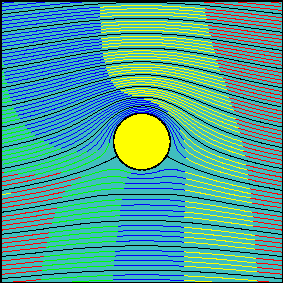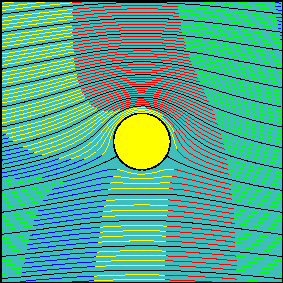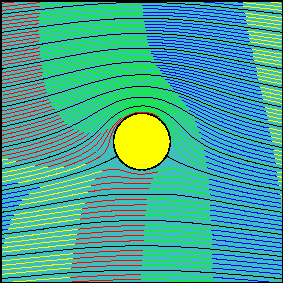
The grid of smoke sources is equally spaced in the vertical direction and it is positioned far upstream from the body (at a distance of about 100 times the radius of the cylinder), so that sources are not influenced by the body (uniform flow). Animations have been realized for three increasing values of the circulation around the cylinder.

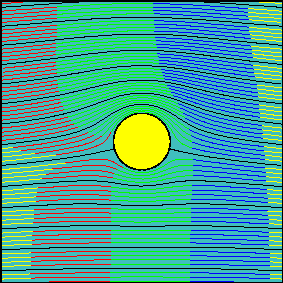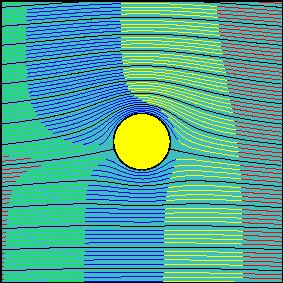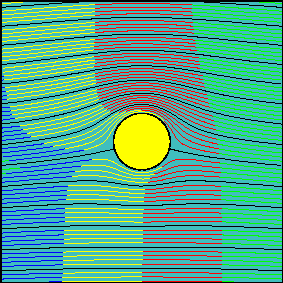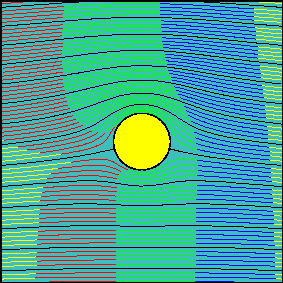
In the first animation the circulation is zero and the flow is symmetrical with respect to the x-axis. Note how the fluid particles closer to the cylinder are delayed with respect to those passing well above (or below) the cylinder. This delay is not due to friction (we are dealing with an inviscid fluid) but to the fact that near the stagnation points velocity tends to decelerate to zero speed. Due to the symmetry of the flow field, if two particles start symmetrically with respect to the x axis, they will need the same amount of time to flow around the body.

When circulation is increased, the latter statement is not true anymore. Now, the fluid flowing above the cylinder reaches the downstream section before the fluid flowing below the cylinder. It is possible to demonstrate that the arrival times are the same only for two particles starting slightly above and below the front stagnation point and flowing along the cylinder surface.

In many elementary aerodynamics textbooks it is stated that, with non-zero circulation, the portion of fluid flowing above the cylinder is accelerated with respect to the one flowing below it ``because it must travel for a longer route to reach downstream in the same amount of time''.

In reality there is no physical law imposing that the two fluid portions flowing above and below the cylinder (the interface of which can be identified with the streamline passing through the two stagnation points) must take the same time to travel around the cylinder.

Indeed, looking at the second animation, it is evident that far from the body, where the flow is essentially uniform, the ``above-the cylinder'' fluid reaches the left end of the window well before the ``below-the cylinder'' fluid does. If we were allowed to observe what happens far downstream, where the flow is certainly uniform again, we would see that this configuration is somewhat ``frozen'' and the fluid particles which have been delayed do not try in any way to catch up.

In the cases examined so far, it is nevertheless still true that two adjacent fluid particles that are separated by the body will become adjacent again once the body is passed, since the arrival times of two particles flowing along the cylinder surface are the same. In the case of flow around an airfoil even the latter statement is true only for a very peculiar case.