We now analyze the case of the so-called hydrodynamic dipole, that results from the superposition of a source and a sink of equal intensity placed symmetrically with respect to the origin. The analogy with electromagnetism is evident. The magnetic field induced by a wire in which a current flows satisfies equations that are similar to those governing irrotational plane flows.

The complex potential of a dipole is

if the source and the sink are positioned in (-a,0) and (a,0) respectively.

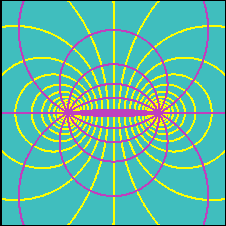
Streamlines are circles, the center of which lie on the y-axis and they converge obviously at the source and at the sink. Equipotential lines are circles, the center of which lie on the x-axis.