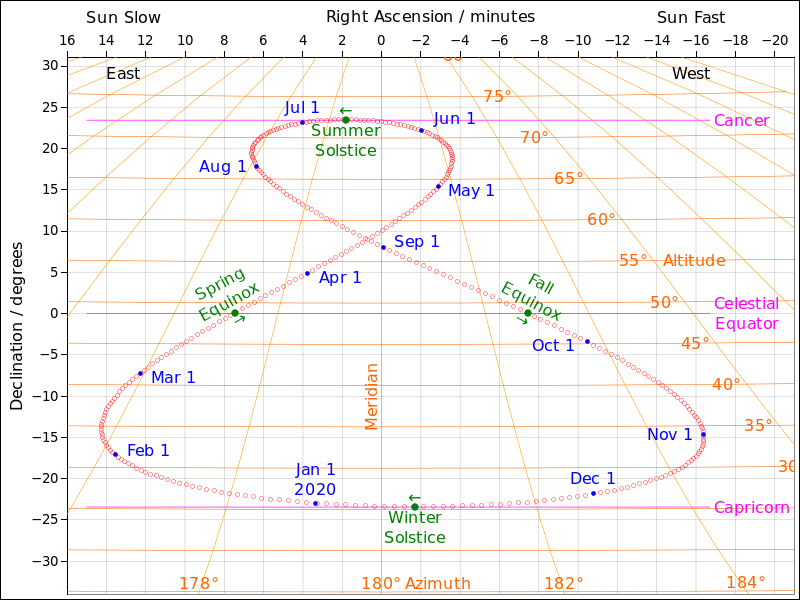
Figure 1: Analemma and Equation of Time
The diagram shows the position of the sun in the sky at noon, local mean time. This figure-8 shape is called an analemma.
The horizontal scale of the diagram is magnified about 10× (relative to the vertical scale) for clarity.
The primary axes (shown in black, with gray grid lines) are minutes of right ascension and degrees of declination. In this system, the celestial north pole is at +90∘, and the celestial equator is at 0∘.
In addition, the orange grid lines show another coordinate system, namely the local horizontal system, in degrees of azimuth and degrees of altitude. In this system, the zenith is at +90∘, the horizon is at 0∘. In this part of the sky, the celestial equator is above the horizon by an amount equal to the observer’s colatitude.
The north-south component of this diagram pertains to the seasons.
The east-west part of this diagram is called the equation of time. In early November, the sundial is ahead of local mean time by about 16½ minutes. In mid-February, the sundial is behind by just over 14 minutes.
In what follows I use the German word Etmal, which unambiguously refers a full day, namely the period from one noon to the next (approximately 24 hours). This stands in contrast to the ambiguous English word day, which could be one Etmal or could be just the daylight portion thereof. (A sidereal day is unambigously 24 sidereal hours.)
The earth spins at a uniform rate, to an excellent approximation, so the sidereal day is always the same. In contrast, the Etmal gets longer and shorter. More than half of that is due to obliquity: the plane of the earth’s orbit is inclined relative to the plane of the earth’s rotation (i.e. the equatorial plane); this accounts for the basic figure-8 shape. Slightly less than half is due to eccentricity: at various times of the year, the earth moves faster or slower in its orbit, because the orbit is elliptical (not circular). There’s a nice graph of the two contributions in reference 1.
The longest Etmal of the year occurs at perihelion, which is in the first week of January each year. The shortest Etmal occurs at aphelion, which is in the first week of July.
The shortest daylight of the year occurs on the solstice, but this is not the latest sunrise or the earliest sunset. That’s because the sunrise and sunset are both getting later, rapidly, during this part of the year. You can see that the dots in the diagram are moving to the east. As a result, the earliest sunset is a few days before the solstice, and the latest sunrise is a few days after.
All the data in the diagram was computing using a python program that depends on Skyfield2 library routines. It is not an “artist’s conception”. (There were of course many cosmetic decisions about styling and labeling.)
For a couple of centuries, navigation depended on having a chronometer that was synced to GMT. To actually use the thing, you needed an ephemeris with the equation of time, so you could convert mean time to/from solar time. A 16 minute discrepancy corresponds to 4 degrees of longitude, which corresponds to a couple hundred miles (at middle lattitudes).3
You also needed the chronometer to keep time at a steady rate, and you needed to know what the rate was, very accurately. So before each voyage, you got a “rating” certificate from the local astronomer.
When I was in elementary school, I read a story that went like this: On a Nantucket evening in 1832, a sea captain is horrified to find that the astronomer is out of town. He can’t afford to wait. However, the astronomer’s 14-year-old kid says she can do the rating.4 She has enough cred that he lets her do it. And he pays her.
I was quite smitten by this story. It was interesting that a piece of paper, more-or-less pure scientific information, was a matter of life and death. It was also the first time I’d seen a business model where a scientist could get paid for doing science (not involving teaching, manufacturing, et cetera). I dreamed of a world where people were treated with respect without regard to age, sex, formal credentials, or anything else.