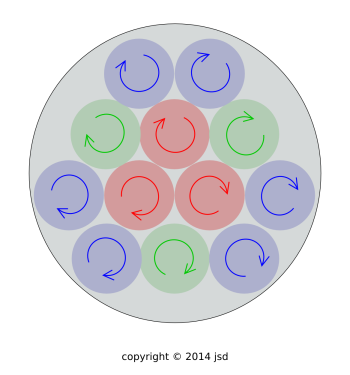
Figure 1: Vorticity in a Spinning Cylinder, End View, Plain
There is a theorem that says if you define things properly, vortex lines cannot end. This is not even a law of physics, but rather a mathematical theorem. In any situation where vortex lines seem to end or disappear, it is worthwhile to figure out where they really went. The math is discussed in section 2, but first let’s look at the physics. Let’s try to understand why the result is useful, not just a mathematical curiosity.
Let’s start with a cup of coffee. More specifically, let’s consider a mug of coffee, in the form of a short squat cylinder. Rather than stirring it with a spoon, let’s set the whole thing on a turntable so that it undergoes uniform rotation. This is not quite the same as a vortex, as we can see from the following contrast:
| Uniform Rotation | Ideal Vortex |
| Uniform rotation has |v| proportional to ρ, where v is the velocity, and ρ is the distance from the axis of rotation. In other words, ρ is the norm of the projection of r onto the plane of rotation. | An ideal vortex has |v| proportional to 1/ρ. |
| A fluid (or anything else) undergoing uniform rotation has vorticity Ω = 2ω everywhere, where ω is the angular rate of rotation. | An ideal vortex has a delta function of vorticity in the middle, and zero vorticity everywhere else. |
Specifically, uniform rotation can be approximated as a whole bunch of little vortices. A first approximation is shown in figure 1. You could make a better approximation by having a larger number of weaker vortices.
Here the vorticity is traditionally defined as the vector
| (1) |
although it may be better to think of it as the bivector
| (2) |
Now we take an important step: We define v(r) to be the velocity of whatever is at location r, be it coffee or air or whatever. We do not restrict r to be inside the mug. I suppose you could restrict it, but there is no advantage in doing so. Leaving it unrestricted is highly advantageous, as will become apparent in a moment.
Since the mug and the coffee are undergoing uniform rotation, we can simplify the picture by replacing them with a solid cylinder. Then we can simplify things even further by getting rid of the turntable. We imagine that the cylinder is hanging by a thread, spinning in mid-air.
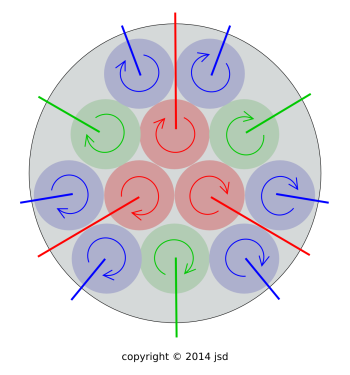
Let’s consider what happens if the air surrounding the cylinder is stationary. Then there will be a tremendous shear layer near the boundary of the cylinder. The situation on one end of the cylinder is shown in figure 2. The straight radial lines represent vortex lines. The lines run parallel to the axis from one end of the cylinder to the other (not shown), then pop out the end, run along the sides of the cylinder inside the shear layer, then re-enter the cylinder at the opposite end.
|
| |
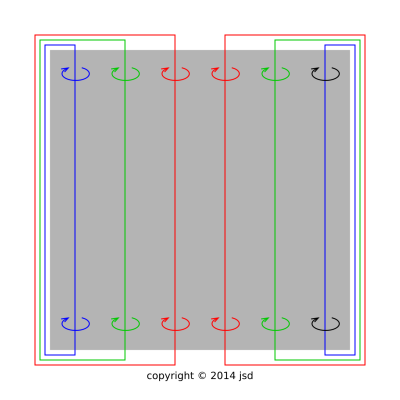
| Figure 2: Spinning Cylinder, End View, Endless Vortices | Figure 3: Spinning Cylinder, Side View, Endless Vortices | |
Figure 3 shows a side view of the situation. This shows more clearly how the vortex lines pop out one end of the cylinder, run along the sides of the cylinder, and then re-enter via the opposite end.
Things get really interesting if the air mass is moving relative to the cylinder. There is a basic principle of fluid dynamics that says the vortex lines get carried along by the fluid. As surely as a puff of smoke gets carried by the wind, a tornado gets carried by the wind. This is shown in figure 4, subject to a few minor simplifications.
The bundle of vortex lines on the left side of the diagram is called the starting vortex. It tells us something about where the cylinder was (relative to the air mass) when it started spinning. Let’s not worry about it.
Figure 4 is interesting because there is a force on the cylinder.
The aerodynamic force on a spinning cylinder is known as the Magnus effect.
An ordinary airplane wing does not spin; it uses other means to produce circulation in the air. The key points is that the vortex lines that are created are endless.
So, here’s the punch line: If you stir up a vortex in a cup of coffee, you can see the vortex in the liquid rather easily. You cannot so easily see how the vortex line continues into the air. Nevertheless, it does continue. Keeping track of the continuation allows you to understand a lot of things, including the aerodynamic forces on sports balls, airplane wings, et cetera.
The idea that vortex lines never end can be explained mathematically as follows. Pick any one (or all) of the following:
| (3) |
where v is the velocity. Actually I’m pretty sure that
| (4) |
where Q is almost any vector field.
To say the same thing without cross products:
| (5) |
where Z is almost anything whatsoever, vector or otherwise.
We can also write
| (6) |
which is equivalent to equation 5 by definition (i.e. the definition of “d” i.e. the exterior derivative).
That simplifies to the operator equation
| (7) |
In words, equation 7 says “the boundary of a boundary is zero”. For example, the topographic contour lines on a landscape do not end. You can make contours on a map “seem” to end by cutting the map, but the map is only a representation of the physical landscape, which is unaffected by such chicanery.
The result depends on the equality of mixed partial derivatives and not much else.
In particular, you should not assume that vortex lines end when they come to the boundary of the medium. Most likely they keep going, either by burrowing into the boundary layer or by extending out of one medium into another.