This violates the letter and spirit of the third law. A force is just a force. It is not just unnecessary but actively misleading to introduce the notion of «agent».
First of all, this embodies a fundamental misconception about vectors. In reality, a vector has a direction and magnitude; it does not have a direction, magnitude, and location.
Secondly, you get into all sorts of trouble if you insist on anchoring vectors by their tails. Sometimes it is better to anchor them by their middles, or to move them somewhere else entirely.
That is a terrible thing to say. In fact, momentum is conserved, period.
In fact, though, all fluids are compressible to some extent, and when we take that into account, we find that Bernoulli’s equation has more to do with enthalpy than energy.
Authors should be allowed to define their terms however they like, within reason, but this is unreasonable. To the extent that «thermal energy» can be defined at all, it needs to include the potential energy as well as the kinetic energy of the atoms and molecules. In a solid, half the heat capacity comes from potential energy, and half from kinetic energy.
Gaaack!
There are definitely not two kinds of charge. If there were, we would need two variables: one to keep track of the “resinous electricity” and another to keep track of the “vitreous electricity”. In fact, we keep track of a single charge variable, which can be positive or negative. For details on this, see reference 1.
This was figured out by Watson (1747) and independently by Franklin (1747). Indeed, Franklin introduced the terms “positive”, “negative”, and “charge” for precisely this reason, to indicate a surplus or a deficit of the one type of electricity. See reference 2.
Ironically, in the book, the 3D diagram – which is harder to draw – is drawn much more accurately.
See also reference 3.
|
| |
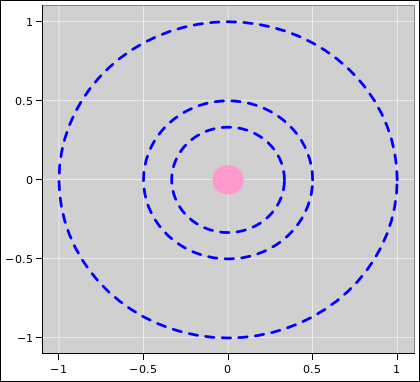
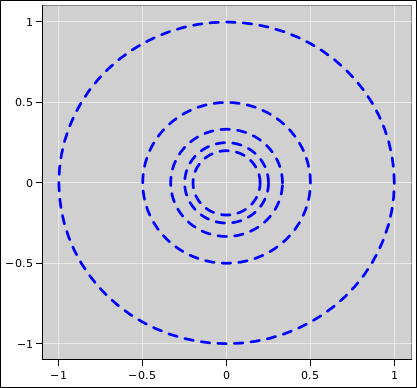
| Figure 1: Equipotentials V=1, V=2, and V=3 for the 1/r Potential | Figure 2: Equipotentials V=1 through V=5 for the 1/r Potential | |
It would be even better to show more contours, as in figure 2.
Secondly, in the elevation graph, it would be better to use a louder color and/or a heavier line to emphasize the contours of constant V. As it is, they are hard to untangle from the contours of constant x and y. Also, given that the plot goes higher than V=4, the fourth contour really should be shown.
The text says «The potential outside the charged sphere is the same as the potential of a point charge at the center.» That’s quite wrong. That’s the worst sort of equation-hunting, i.e. applying an equation in a situation where it is not valid. It leads to getting an answer that is wrong by a factor of infinity.
There is a theorem about a spherically-symmetrical static distribution of charge, but that’s not what we have here, because of the image charge induced by the proton. At zero distance, the induced-dipole interaction is infinitely stronger than the first-order Coulomb interaction. The text ignores this infinitely-large contribution.
One familiar counterexample is any electrical transformer, which depends on the voltage not being a potential. Another example is a betatron. This is perhaps less familiar, but it makes the basic physics particularly obvious.
Similarly in the un-numbered equation in the middle of page 894: it does not make sense to define things in such a way that a minus sign appears in the statement of Ohm’s law. This misbegotten minus sign crops up again and again throughout the chapter.
We are reminded of this at the top of page 898.
This will come as a surprise to every electrical engineer in the world.
I suppose it is “legal” for an author to define a notion of «conservation» as applied to current that is not parallel to the notion of conservation as applied to everything else ... but it’s amazingly bad pedagogy.
- For starters, you might think it makes the subject twice as difficult as it needs to be, because now students need to learn two different notions of «conservation» rather than just one.
- Really, though, it’s much worse than that. If students had to
learn two separate definitions (conservation of charge and
blorkivation of current) that would be twice as much work as
necessary ... but if they have to learn two ideas that share the
same name it imposes the additional burden of confusion
... utterly needless confusion.
This is on top of the pre-existing painful confusion involving the physics notion of conservation as opposed to endangered-wildlife conservation.
A major goal of the course is for students to develop a solid understanding of conservation. This is immediately applicable to charge, energy, momentum, and angular momentum. It can eventually be extended to other things such as lepton number. It can be approximately extended to yet other things, such as the conservation of the number of carbon atoms during a chemical reaction.
The idea referred to in the previous paragraph cannot be extended to current, not even approximately. Here’s a counterexample: the current in an RC circuit just dies away. It doesn’t flow away into some nearby region; the current just stays in place and decreases. Momentum cannot do the analogous thing, because momentum is conserved.
Here’s another counterexample: Consider a photodetector or perhaps a Geiger-Müller tube. It contains some substance subject to an electric field. Initially there is no current. Then a photon comes in and ionizes the substance. Now there is a current, because the negative ion goes one way while the positive ion goes the other way. This current did not come in from outside; it just appeared in place, violating any reasonable notion of conservation of current.
It is a serious disservice to students to speak of «conservation of current» in the same breath as conservation of charge. It seriously undercuts one of the major goals of the course.
The idea that the current is the same everywhere along a given wire already has a perfectly good name, Kirchhoff’s Current Law. This is a corollary of conservation of charge, in the DC limit. The existence of a good name makes it all the more insane to use an abusive name such as «conservation of current».
In other words, we are told that current is conserved and energy is not. That’s two misconceptions in a single sentence.
See also item 21.
In my universe, conservation of energy is of the utmost importance. It is hard to imagine anything more fundamental, more emblematic of the the unity and grandeur of physics.
We already have a problem because students are confused by the ambiguity and contradiction between the physics energy and the “DoE energy”. The latter is some kind of loosely-defined “useful energy” or “available energy”. If the physics teacher starts throwing around the word “energy” in such a way that it does not refer to the physics energy, things get real ugly real fast.
Even if we pretend the statement on page 896 refers to conservation of charge, it amazes me that anyone could make such a statement without noticing that energy is conserved, just as strictly as charge. So it seems off-the-wall to use conservation ideas to assert that energy is used up whereas charge (or current!?!) is not.
The thousand-pound moose on the table is entropy. The only thing in this scenario that is irreversibly used up is the non-entropy. This is not mentioned – not even hinted at – in Knight or in Chabay & Sherwood.
When the DoE-energy gets used up, it is not for reasons having anything to do with the physics energy. The physics energy is still there. It may perhaps become less-available and less-useful, but that’s because of entropy, to the extent that it can be quantified at all.
The true physics is very easily explained by saying that the electrical resistor is creating a lot of entropy. This is incomparably better than replacing one wrong idea (current used up) with another wrong idea (physics energy used up).
This is important, because there is value in applying Kirchhoff’s Junction Rule – aka Kirchhoff’s Current Law – to the junction between the two resistors.
A more correct statement appears on page 900.
The part about fixed and unvarying potential differences is contradicted on the next page. The part about fixed and unvarying EMF is repeated on the next page, but is not true in real life.
Statements that are restricted to ideal batteries should say so.
Hint: Rechargeable battery.
There is no chance that students will be able to answer this question correctly. Incandescents are infamously non-Ohmic. See also item 26.
What’s worse, on page 1009, it says the calculations «aren’t quite right» because they «are based on Galilean relativity». Let’s be clear: There is nothing wrong with Galileo’s principle of relativity, as he stated it in 1638. Indeed the calculations on pages 1008-1009 are not quite right ... but that’s for reasons having nothing to do with Galileo.
| (1) |
We remark in passing that it would make a lot more sense to use an actual derivative, rather than a ratio of finite deltas.
However, the main point is that the book doesn’t do anything useful with this formula. Instead, it immediately converts it to an expression involving the 3-velocity and a factor of gamma, namely equation 36.33. The rest of the discussion emphasizes the latter.
Furthermore, explicitly labeling the transition metals as «d» and the lanthanoids as «f» is a step in the wrong direction. A lot of people who ought to know better think there should be 14 “f block” elements, but there is no data to support this. The set of integers from 0 through 14 inclusive has 15 members. People who cannot reliably count to 15 should not be telling other people how to do quantum mechanics. For details on this, see reference 4.