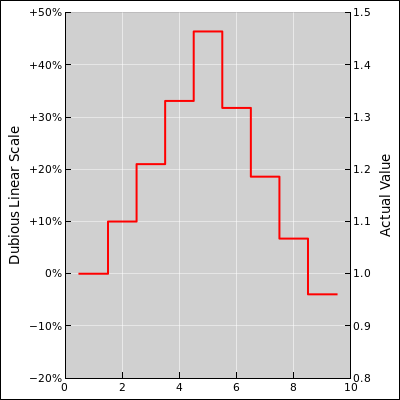
Figure 1: Dubious Linear Scale : Percent
There are situations where thinking in terms of a percentage is problematic, and centineper (cNp) works better, especially when the range of variation is bigger than a few percent. For example, suppose we are measuring something that might change by an amount proportional to the previous amount. This could be radioactive decay, compound interest, stock market fluctuations, the spoilage of milk, or the spread of a pandemic.
This applies to how we formulate our thoughts, as well as communicate our thoughts. In particular, it applies to the units on log and semi-log plots.
Here’s a simple example:
We can eliminate the ambiguity by saying that 51% is 2 cNp bigger than 50%. Adding two cNp is always the same as multiplying by 1.02.
This illustrates how cNp can help, even when the percentage of change is small. When the changes are larger, there are additional benefits, as discussed below.
Here’s a fancier example: Suppose a certain quantity starts out with a value of 1, on Day One, and then goes up by 10% each day for four days. So we multiply by 1.1 four times. The overall result is not a 40% increase from where we started, but rather a 46.5% increase. This can be explained in terms of compound interest (as opposed to simple interest). The fourth step increases by 10% of the Day Four value (not the Day One value). This scenario is shown by the upward steps in figure 1.
Continuing with our example, suppose that the quantity now goes down in steps of 10% per day for four days. That is, we multiply by 0.9 four times. The last increase was 10% of the Day Four value, but the first decrease is 10% of the Day Five value, which is larger. Each decrease is larger than the corresponding increase. At the end of the whole process, we end up significantly below where we started.
These eight steps can be applied in any order, and the final outcome is the same. Multiplication is commutative.
Let’s be clear: The 40% tick-mark in figure 1 is 40% above where we started on Day One, but it is not 10% above the 30% tick-mark. This causes endless confusion.
Things work out better if we think in terms of centinepers instead of percentages. A neper is a logarithmic unit, like a bel (as in decibel), pH units, or Richter units. It measures relative change. The neper is abbreviated Np, and a centineper is abbreviated cNp. Specifically:
| (1) |
In Figure 2, we make a series of proportional changes, going up and then back down in steps of 10 cNp. Things are much simpler when we formulate and communicate our ideas in terms of cNp, as you can see by comparing this figure to the previous one.
Adding 10 cNp and then subtracting 10 cNp gets you back to where you started, exactly. Addition is commutative.
An increase of 1 cNp is very slightly larger than 1%, while a decrease of 1 cNp is very slightly less of a decrease than 1%:
| (2) |
For larger changes, the distinction becomes more noticeable:
| (3) |
A 40 cNp increase is very nearly a 50% increase, while a 40 cNp decrease is very nearly a decrease of 33⅓%.
| (4) |
Here’s another useful fact: There are 69 cNp per octave:
| (5) |
The definition of neper is very similar to the defintion of bel, except that a bel refers to power. In a linear circuit, a tenfold change in power is 10 dB by definition, but a tenfold change in voltage is 20 dB (since power is proportional to voltage squared). Unlike a bel, a neper is a factor of 10 in whatever quantity you are measuring.
Here’s a good rule of thumb: If you are using a logarithmic axis, thinking in terms of percentages is usually a mistake. Nepers work better. (You might get away with percentages if the total range of variation is small, i.e. less then a few percent.)
Similarly: Any time the difference between compound interest and simple interest is important, nepers work better than percentages.