|
| |
| Figure 1: Short-Range Couplings | Figure 2: Long-Range Net Interaction | |
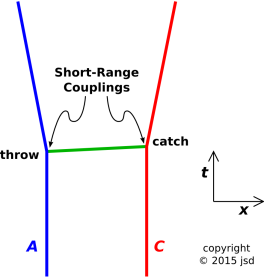
Suppose we have two people, Azura (shown in blue in figure 1 and Cerise (shown in red in the figure). They are both standing on the ice rink, wearing ice skates. As usual, we choose ice skates because of their famously low friction.
Initially, they are a moderate distance apart. They are just standing there, facing each other, not moving, just progressing toward the future at a rate of 60 minutes per hour.
At some point, Azura picks up a baseball and throws a 90 mile-per-hour fastball toward Cerise. In accordance with the third law of motion, i.e. conservation of momentum, the act of throwing imparts rightward momentum to the ball, and an equal amount of leftward momentum to Azura. So she starts moving backward, towards the left in figure 1.
A moment later, Cerise catches the ball. The ball transfers most of its momentum to Cerise. If we make the approximation that the mass of the ball is negligible compared to the mass of the persons, the ball transfers all of its momentum. In any case, Cerise starts moving backward, towards the right in figure 1.
Note that the throw was performed using nothing but short-range forces, namely the force of contact between hand and ball. The same goes for the catch.
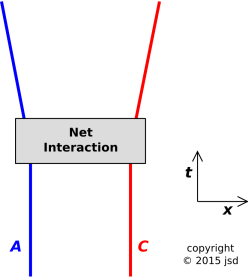
We can describe the same situation in dramatically different terms if we look at figure 2. We use the so-called black-box approach. There is a black box labelled “Net Interaction” and we choose not to look inside the box. All we see is that Azura must have exerted a force on Cerise, and Ceries must have exerted an equal-and-opposite force on Azura. The net interaction can reasonably be described as a long-range interaction. The two persons exerted force on each other, even though they were not close enough to touch each other directly. Nowhere near close enough.
If you look closely enough, you might be able to figure out what happened, because the baseball is in a different location before and after, but let’s pretend we didn’t notice that. Or perhaps there was a symmetrical exchange of baseballs, as shown in figure 3
It must be emphasized that everything in figure 1 is local in time and space. The throw happens at a particular time and place, the catch happens at a particular time and place ... and in between, the baseball moves nicely and smoothly; it does not magically move from one place to some other far-away place.
Our parable applies to physics as follows: Consider the contrast:
| In some fundamental sense, everything in physics happens locally. It’s all short-range, by which we mean zero-range. Strictly speaking, there are no long-range forces. There is no long-range anything. This is pretty much required by special relativity plus basic notions of causality. | To a reasonable approximation, it is possible to speak of long-range interactions, provided we consider only the net interaction, and provided we don’t look too closely. This is the black-box approach. |
| Sometimes you can make progress in physics by ripping open the black box to see what’s inside, to figure out the nitty-gritty details. | Sometimes you can make progress in physics by taking the black-box approach. Sometimes you don’t need to know the details. Borrowing an idea from Galileo, Newton famously said Hypotheses non fingo ... which was his way of saying I don’t know about the details, and I don’t care, and it doesn’t matter. |
Let’s spell out the analogy in detail. The electric field is a classic example of a so-called long-range interaction, if we look only at the net interaction, without peeking inside the black box. For example, the two leaves of an electroscope repel each other, even though they are not touching.
On the other hand, if we rip open the black box, we see nothing but local processes. The charge on one leaf gives rise to an electric field, by strictly local zero-range processes. After a short amount of time, the electric field extends out to enormous distances. The electric field couples to the charge on the other leaf, coupling by strictly local processes.
The electrostatic situation is symmetrical, because each charge gives rise to a field that influences the other, as indicated in figure 3.
The black-box approach always depends on some assumptions. For example, in figure 2, it was assumed that are interested in the people, and not particularly interested in the baseball. That’s OK; there are objective reasons for considering people and baseballs to be different.
When we extend this idea to particles and fields, we need to be careful, because fundamentally they’re all just fields.
Note the similarities and contrasts:
| Each photon is a particle; it is an excitation of the Maxwell field, i.e. the electromagnetic field. | Each electron is a particle; it is an excitation of a certain Dirac field. |
| The photon has zero mass. | The electron has a mass of approximately 511 keV. |
| The electromagnetic interaction is mediated by the exchange of photons, as in figure 2. Even though the coupling is always local (zero range), the net interaction can extend out to very long ranges, to interplanetary distances and beyond. It works just the same for rather small distances, within molecules, within atoms, and even within nuclei. | There are other processes that involve the exchange of electrons. The coupling is, of course, strictly local (zero range). The process does not give rise to long-range forces under ordinary conditions; typically it doesn’t extend more than one Ångstrom or so. |
| This explains why a good radio works over enormous distances. | This explains why atoms and molecules are the size they are. It explains why ordinary matter is not easily compressible. |
Here’s a contrast of another kind:
Terminology: When people talk about “contact forces” or “short-range forces” they are not talking about the couplings that go on inside the black box; those are always zero-range. The typical “contact force” arises when objects get so close that the atoms are touching, and electron-exchange processes become important, in combination with the usual electromagnetic processes.
Let’s be clear:
| In the electroscope example, electrons interact by the exchange of photons. | Meanwhile, the size of atoms is determined by another process that involves the exchange of electrons. |
| When photons pass near the sun, they interact with it via gravity. |
So, you can see that it is a fool’s errand to try to categorize things as objects versus interactions. What’s the object in one scenario is the interaction in another.
| Scenario | “Object” | Exchanging | ||
| Electroscope | electrons | photons | ||
| Chemical Bond | atoms | electrons | ||
| Gravitational Lens | photons | gravitons |
You can, if you choose, talk about matter and interactions and objects and particles and waves and so on. All of those are things, but they are not distinct things! Pretty much all of those things can be explained in terms of fields.