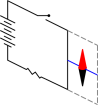
Figure 1: Compass and Turned-Off Electromagnet
Once upon a time, there was a kid named Pierre who was fascinated by the symmetries and apparent asymmetries of electromagnetism. In particular, he was really bothered by the apparatus shown in figure 1. Initially the compass needle lies in the same plane plane as the electrical circuit. It is supported by a torsion fiber. This allows the needle to rotate in the direction perpendicular to the fiber, but provides a restoring force that (in the absence of magnetic forces) favors the symmetric configuration as shown. To summarize: everything appears to be completely reflection-symmetric and non-chiral.
Then close the switch! A magnetic field is created in the neighborhood of the wire. The compass needle rotates out of the plane of the circuit, as shown in figure 2. The apparatus has lost its reflection-symmetry. It is now chiral, like a screw-thread.
It is fairly common to have a physical situation where the solution to the equation of motion is less symmetric than the equation itself. Tossing a coin is an example. The equation of motion doesn’t favor heads or tails. The equation and the initial conditions are up/down symmetric, but after the toss is completed, the coin will either be heads-up (which is not an up/down symmetric state) or tails-up (also not an up/down symmetric state). The average outcome is symmetric, but any particular outcome has broken symmetry.
The situation in figure 2 is very, very different. There is nothing random about it. The red end of the compass needle will rotate to the same side of the plane every time. This is not a randomly broken symmetry, this is a systematically broken symmetry.
Pierre could not understand how something that was initially symmetric could suddenly become less symmetric.
So, here’s the puzzle: What’s going on here?
Hint: You’ve got basically two possibilities:
See reference 1 for the answer to the puzzle.
Pierre asked his teachers about this, but nobody could give him a satisfactory answer. Fortunately, Pierre didn’t let himself be derailed by this frustration. He filed the problem away in his brain, and went on to work on other things (reference 2) for a while.
He never gave up on the magnet symmetry problem. He worried about it off and on for about 20 years before finally figuring it out. Along the way he learned a few interesting things about symmetries in general, and about the inner workings of bar magnets.
Symmetries have continued to be an important part of the foundations of physics. See for example reference 3, reference 4 and reference 5.
English translation: “On symmetry in physical phenomena, symmetry of an electric field and of a magnetic field”