Figure 1: Uniform Acceleration of the Reference Frames
Note: The related topic of coordinate systems is discussed in reference 1.
There is a conflict in terminology concerning “inertial” reference frames. The term means different things to different people:
|
In the context of modern (post-1900) physics, the term
“inertial reference frame” refers to a freely-falling frame. In such a frame, the local gravitational field is necessarily zero. |
In the context of classical (pre-1900) physics (which includes most high-school physics and introductory-level college physics), the term “inertial reference frame” is not always as clearly defined as one would like. Usually the term seems intended to cover frames in which the basic laws of motion are valid, in their usual simple form, including (possibly) a nonzero gravitational field … but that is too vague to be a workable definition. |
| To avoid confusion, it is best to avoid the term “inertial frame” entirely, except perhaps in situations where gravitational effects are negligible. |
| Freely-falling frames are sometimes called unaccelerated frames, in the sense that any freely-falling frame is unaccelerated relative to any other nearby freely-falling reference frame or freely-falling object. However, this is risky because folks who prefer the pre-1900 viewpoint like to think that their frames are unaccelerated, ignoring the gravitational acceleration. | It is usually fairly easy to avoid the term “inertial frame”. For example, if you wish to refer to the usual terrestrial laboratory frame, you can just say “terrestrial laboratory frame”. Closely related is the earth-centered earth-fixed (ECEF) frame. Below we will attempt to define a notion of “Newtonian frame” but this is not so easy. |
| It is an immediate corollary of the definition that any frame moving with uniform velocity relative to a freely-falling frame is also a freely-falling frame, at least locally. This is Galileo’s principle of relativity. | It is an immediate corollary of the definition that any frame moving with uniform velocity relative to a Newtonian frame is also a Newtonian frame. This is another manifestation of Galileo’s principle of relativity. |
We wish to define the notion of Newtonian frame. The following definition is applicable if and only if the overall system is isolated, i.e. not subjected to any outside forces.
We define a Newtonian reference frame as one that is unaccelerated relative to the center of mass of the overall system.
For more on all this, see reference 2.
The usual terrestrial laboratory frame is either the earth centered, earth fixed (ECEF) frame, or some frame that is unaccelerated relative to ECEF.
This is a very important reference frame. ECEF is one of the coordinate systems used by autopilots, flight simulators, and the global positioning system (GPS). Earth-fixed systems are more-or-less obligatory for ordinary terrestrial architecture and engineering. The ECEF system includes centrifugal contributions that are absent from an earth-centered non-rotating (ECNR) frame.
We need to maintain some perspective as to what is important and what is relatively unimportant.
To repeat: the major point is whether you allow your “inertial” frames to include gravity or not. This is a blatant zeroth-order contribution. Because this is an unsettled question, it is best to avoid the term “inertial frame” entirely, lest there be major confusion.
The minor point is that there are at least two ways in which the laboratory frame is not exactly the same as a true Newtonian frame. The rotation rate is not always negligible, as discussed in section 3.2, and the mass of objects in the earth’s field is not always negligible, as discussed in section 3.3.
The Coriolis effect due to the rotation of the earth is extremely significant in geophysical applications including the large-scale circulation of the atmosphere and the large-scale circulation of the oceans. It is significant for long-range ballistics. It can can also be observed in the lab via the precession of a precision gyroscope. It can also be observed using a Foucault pendulum, at any latitude not too near the equator. (Beware that constructing a Foucault pendulum in your lab is a bit tricky. See reference 3 and reference 4 for details.)
Rotation guarantees that the lab frame is not Newtonian. The the usual simple form of the laws of motion does not apply. Coriolis terms must be added.
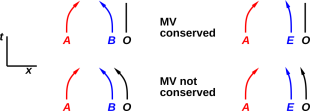
Consider the four scenarios depicted in figure 1. In each case the lines are world lines. The position coordinate runs horizontally, and the time coordinate runs vertically.
| In the upper left corner, we have the world lines of two massive particles A and B. They are initially at rest with respect to one another, but they accelerate toward each other (due to gravity) as time goes on. The observer O is moving parallel to the center of mass (CM) and observes that momentum is conserved, using the conventional MV definition of momentum. | The upper right corner is very similar to the upper left corner, except that one object (E for earth) is much more massive than the other object (A for anvil). When we drop the anvil, it accelerates toward the earth … and the earth accelerates ever so slightly toward the anvil. The observer in this case is moving parallel to the CM, and observes that MV is conserved. It may not be entirely obvious how and why MV is conserved, so the observer might have to say “hypotheses non fingo”. |
| The lower left scenario is the same as the upper left scenario, except that the observer chooses to move along an accelerated path, pacing object B. In this case the observer finds that the MV of object B remains zero, while the MV of object A starts out zero but changes with time. This observer concludes that MV is not globally conserved. (In my opinion, momentum is conserved, but MV is not the right way to calculate momentum.) | In the lower right corner, we have the same scenario except that the observer attaches himself to the laboratory frame, which is attached to the earth. This is ever so slightly different from the CM frame, because the earth accelerates toward the anvil. This observer finds that the MV of the earth remains zero, while the MV of the anvil starts out zero but changes with time. This observer concludes that MV is not globally conserved. |
This lower-right case is a trap for the unwary, because in terms of position and velocity, the observer is “almost” paralleling the CM, since the earth’s path and the CM’s path are “almost” the same … but in terms of MV, this observer does not “almost” get the right answer. His answer is wrong by 100%. That is, 100% of the anvil’s MV is unaccounted-for, in the sense that it cannot be paired with any equal-and-opposite MV in this frame.
To summarize: In all four of these scenarios, the observer is using a Newtonian reference frame, by which I mean a frame that differs from a freely-falling frame by some overall uniform acceleration of the frame. However, MV is globally conserved in only two of these four frames, namely the top two, i.e. the fully Newtonian frames, by which I mean frames that are unaccelerated relative to the CM of the whole system.
Here is a variation on a classic riddle. The following two-part experiment is carried out in an ordinary terrestrial lab frame. It is carried out inside a vacuum chamber, so that we can completely neglect contributions from buoyancy and air drag. We also make sure that there are no significant magnetic fields or electric fields.
| Part 1: We have a hard rubber ball, 10 cm in diameter. | Part 2: We have a lead cannonball, 10 cm in diameter. |
In each case, we drop the ball from a height of one meter onto a smooth horizontal floor. We measure how long it takes to fall, from the moment of release to the moment it touches the floor. The idea is that the two parts of the experiment are identical except that the lead ball is much more massive. The question is, in principle, which ball falls more quickly?
The answer is that the lead ball falls more quickly.
The time difference between the lead ball and the rubber ball may be exceedingly difficult to observe, but in principle the difference exists.
It is easy to see why this must be so, qualitatively, by reversing the roles. We consider each ball to be a very small planet, and we drop the earth onto it, from a height of one meter. The rubber planet has a weaker gravitational field than the lead planet does.
To say the same thing in more quantitative terms, the earth moves. Not only does it move, but it undergoes nonuniform acceleration. When we drop the ball, the ball suddenly accelerates in one direction, while the earth suddenly accelerates in the opposite direction.
This is non-Newtonian behavior, of the same type as illustrated in the lower right of figure 1.
This is just another example from a very wide class of situations in which a reference frame attached to the earth fails to be Newtonian, because of the non-uniform acceleration of the frame.
While we’re on the subject, it should be mentioned that the acceleration of the lab frame is mostly (but not entirely) associated with the law of universal gravitation, which contributes an acceleration equal to G M/r2. The next-largest contribution comes from the centrifugal field due to the rotation of the earth, which is a larger contribution that most people would have guessed. This is locally a uniform acceleration, so it is Newtonian, and is included in the conventional definitions of g, gravity, weight, horizontal, and vertical, as discussed in reference 2.
The previous paragraph applies to the acceleration of an object that is not moving relative to the lab frame. For objects that are in motion, we observe Coriolis effects, which are clearly non-Newtonian, as discussed in section 3.2.
Suppose you have a frame that is not fully Newtonian. In such a frame, the basic laws of motion (in their conventional simple form) are violated to some degree, or are at best inapplicable.
At this point there arise unanswerable – and completely unimportant – questions about which of the three laws of motion are violated.
This is an unacceptable Hobson’s choice situation. You are not allowed to sacrifice one law of nature in order to save another. These issues are more fully discussed in reference 5.
The bottom line is that if you want the laws of motion to hold in their conventional simple form – including the first and second law, and the momentum-conservation law – you must use a fully Newtonian frame. Alas the terrestrial lab frame does not qualify.
In particular, it is hard to conserve MV in the lab frame, since the earth is always at rest (V=0), by definition, in that frame. In the very common case that momentum is transferred from the earth to some other object, there’s a problem.
This is quite a dilemma in introductory physics classes, because everybody “wants” to use the lab frame, and everybody “wants” the simple laws of physics to hold.