In the last example, we superimpose to the complex potential that gives the flow around a cylinder a vortex of intensity positioned at the center of the cylinder. The resulting potential is

The presence of the vortex does not alter the streamline describing the cylinder, while the two stagnation points below the x-axis.

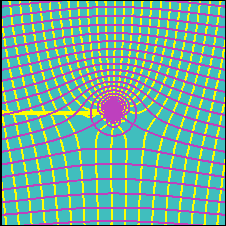
The streamlines are closer to each other on the upper part of the cylinder and more distant on the lower part. This indicates that the flow is accelerated on the upper face of the cylinder and decelerated on the lower part, with respect to the zero circulation case.

The resulting flow field corresponds to the case of a rotating cylinder, which accelerates (with respect to the case of no circulation) fluid particles on part of the cylinder and decelerates them on the remainder of the cylinder.

Note the presence of a discontinuity in the potential function (thick yellow line on the left) that is related to the fact that the vortex potential (as mentioned in a previous section) has a nonzero cyclic constant.