 |
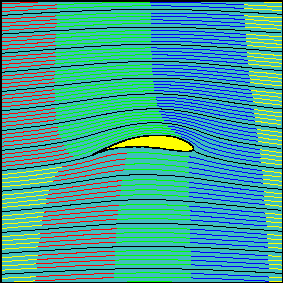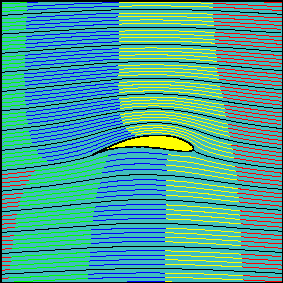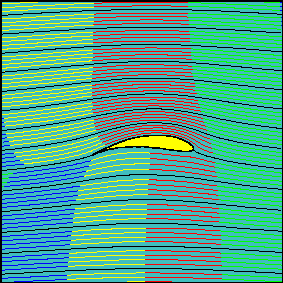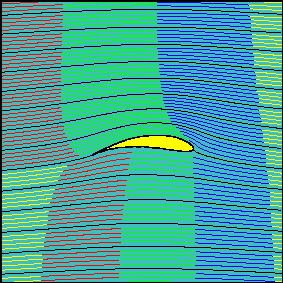
In the following animations the streaklines generated by a set of smoke sources equally spaced in the vertical direction and positioned far upstream of the airfoil are presented. The color of the injected smoke has been changed at regular time steps so as to make the time history of the fluid particles that have been ``marked'' passing through each smoke source visible.
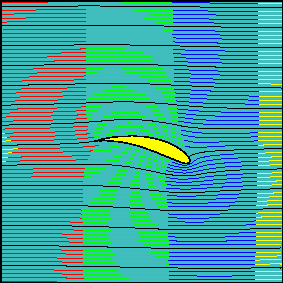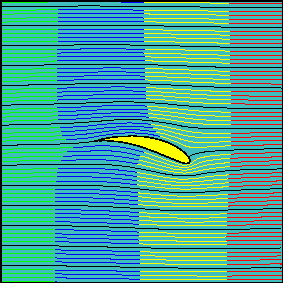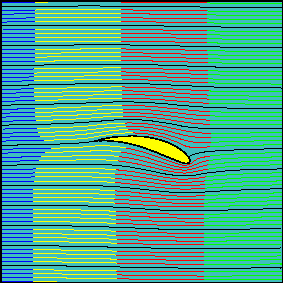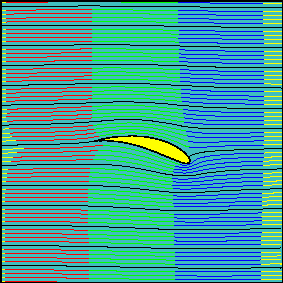
Three increasing values of the effective angle of attack (0, 15 and 30 degrees, respectively) have been chosen for the animations.
The first animation shows a smoke pattern similar to that observed for the flow around a cylinder with no circulation. Indeed, in this case the rear stagnation point is naturally coincident with the trailing edge and the Kutta condition is verified with zero circulation around the airfoil.
 |
Note how the fluid particles closer to the airfoil are delayed with repect to those passing well above (or below) the airfoil. Friction has no role here and this effect, as for the cylinder, is due to the vanishing of velocity in the neighborhood of the stagnation points. Also note how the two portions of fluid passing above and below the airfoil reach the left end section at the same time. Two fluid particles flowing along the profile need the same time to travel above or below the airfoil.
As the angle of attack, and so the circulation around the airfoil, is increased, the latter statement is not true anymore, in the sense that fluid flowing above the airfoil reach the downstream section earlier than the fluid travelling below it.
 |
 |
It can be demonstrated that in contrast to what happens for the cylinder, the travelling times are in this case different also for fluid particles flowing along the airfoil surface, as it is evident looking at the animations above and focussing on the neighbourhood of the trailing edge.
This effect is related to the role played by the conformal transformation, which alters both the length of the path and the velocity but not in a way to keep the travelling times of two particles flowing along the surface of the airfoil equal.
The fluid portion flowing below the airfoil is delayed with respect to the portion flowing above it, and the delay increases as the angle of attack (and so the circulation around the airfoil and, as we will see, the lift) increases.
Stating that the fluid flowing above the airfoil is accelerated with respect to the fluid flowing below it ``because it must travel for a longer route in the same time'' is then definitely wrong.


