FLOW AROUND AN AIRFOIL

Before analyzing the velocity and pressure field for the case of an airfoil, we need to investigate a little more deeply the role played by circulation.

The Kutta-Joukowski theorem shows that lift is proportional to circulation, but apparently the value of the circulation can be assigned arbitrarily.

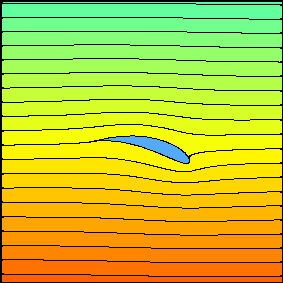
The solution of flow around a cylinder tells us that we should expect to find two stagnation points along the airfoil the position of which is determined by the circulation around the profile. There is a particular value of the circulation that moves the rear stagnation point (V=0) exactly on the trailing edge.

This condition, which fixes a value of the circulation by simple geometrical considerations is the Kutta condition.

Using Kutta condition the circulation is not anymore a free variable and it is possible to evaluate the lift of an airfoil using the same techniques that were described for the cylinder. Note that the flow fields obtained for a fixed value of the circulation are all valid solutions of the flow around an airfoil. The Kutta condition chooses one of these fields, one which represents the best actual flow.

We can try to give a feasible physical justification of the Kutta condition; to do this we need to introduce a concept that is ignored by the theory for irrotational inviscid flow: the role played by the viscosity of a real fluid.

Suppose we start from a static situation and give a small velocity to the fluid. If the fluid is initially at rest it is also irrotational and, neglecting the effect of viscosity, it must remain irrotational due to Thompson theorem.

The flow field around the wing will then have zero circulation, with two stagnation points located one on the lower face of the wing, close to the leading edge, and one on the upper face, close to the trailing edge.

A very unlikely situation is created at the trailing edge: a fluid particle on the lower side of the airfoil should travel along the profile, make a sharp U-turn at the trailing edge, go upstream on the upper face until it reaches the stagnation point and then, eventually, leave the profile. A real fluid cannot behave in this way. Viscosity acts to damp the sharp velocity gradient along the profile causing a separation of the boundary layer and a wake is created with shedding of clockwise vorticity from the trailing edge.

Since the circulation along a curve that includes both the vortex and the airfoil must still be zero, this leads to a counterclockwise circulation around the profile. But if a nonzero circulation is present around the profile, the stagnation points would move and in particular the rear stagnation point would move towards the trailing edge. The sequence vortex shedding -> increase of circulation around the airfoil -> downstream migration of the rear stagnation point continues until the stagnation point reaches the trailing edge. When this happens the sharp velocity gradient disappears and the vorticity shedding stops. This ``equilibrium'' situation freezes the value of the circulation around the airfoil, which would not change anymore.

Let us now proceed to examine the velocity and pressure fields around an airfoil with the aid of some animations showing how they vary when the (effective) angle of attack is changed. In each shot the flow field is obtained imposing the Kutta condition to determine the circulation. A sequential browsing of the following pages is suggested, at least for first time visitors.

Stream lines	Streak lines	Velocity field	Pressure field	Forces on the body