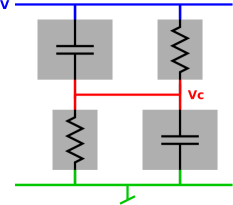
Figure 1: Recommended Circuit Diagram
We start by talking about the black-box approach, which greatly simplifies electrical engineering, software engineering, et cetera.
Later we talk about waves, such as the wave shown in figure 3. This is a perfectly ordinary wave. If you’ve ever wiggled a rope or wiggled an electrical cord you’ve seen waves like this. The wave is interesting unto itself, and we will discuss that ... but then we will use that as a springboard to help us understand other things, including:
These ideas get used throughout science and engineering. They are very deep ideas, but you can understand quite a lot about them as easily as you can understand waves on a rope.
Figure 1 shows the diagram for an almost-normal circuit. (I say “almost” because it’s not really useful as-is, although it is closely related to something useful.)
We say that the circuit has four components: two resistors and two capacitors. The components are connected by three nodes, blue, red, and green.
We choose to treat each component as a black box. That is, we are not concerned with what goes on inside the component; we care only about the behavior that it exhibits at its terminals. This is the appropriate level of detail at the introductory level, and several levels beyond that.
Engineering makes very heavy use of the black-box approach. This includes electrical engineering, software engineering, and a great many other disciplines. Often there are boxes within boxes within boxes.
There is no clear dividing line between physics and engineering, but to a first approximation we could say that physics is used to understand what is going on inside the capacitor, inside the black box. All the details get bundled into a much simpler description, focused on the behavior that is exhibited at the terminals. The black-box description gets exported from physics to engineering.
By way of contrast, consider figure 2. This is not recommended. It represents the same circuit as figure 1, but the emphasis is changed and the terminology is changed, as indicated by the color-code. It doesn’t violate any laws of physics, and it doesn’t violate any biblical commandments, but it violates the black-box model. The red part of the diagram is not a node and it’s not a component. I don’t know what it is. Let’s call it a “blob” for now. It contains the node plus half of one capacitor and half of the other.
Analyzing a circuit in terms of components connected by nodes is simple yet powerful. Focusing attention on the “blob” makes things much more complicated, for no good reason.
You might be tempted by the fact that the “blob” is an equipotential ... but that is not what defines a node. Each node is an equipotential, but the converse is not true. A node is, by definition, the connection between the terminals of the black boxes.
You could say that the “blob” violates Kirchhoff’s circuit laws (as set forth in reference 1), but it would be better to say that those laws simply don’t apply, because they pertain to nodes, and the “blob” isn’t a node.
Here’s another hint, another reminder that the node does not include half of each capacitor: It would be somewhere between insane and impossible to include half of each resistor. The physics of resistors is much more complicated than the physics of capacitors. Interesting and important, but complicated. Don’t open that black box unless you’re sure you want to.
Suppose we have a wave carried by a rope. Some remarks:
| The wave travels from west to east and does not return. | Each bit of rope wiggles in the north/south direction and returns to its starting point. |
Here are a few words of discussion about these points:
We are allowed to look inside the black box if we want to, but we are not required to.
As another way of describing the same process, we speak of introducing a layer of abstraction. In figure 3, the idea of a uniform medium is an abstraction. This stands in contrast to the rope and the chain, which are not abstract at all.
According to the reductionist viewpoint, a wave is “really” just a bunch of rope-particles or chain-particles moving up and down. Also note that the wave cannot exist separately from the medium.
| From the extreme reductionist viewpoint, there is no such thing as a wave; there is just a rope or chain wiggling ways that conspire to make us think there is a wave. | From a non-extreme, moderately-reductionist viewpoint, we accept that the wave is carried by the rope or chain ... but we also recognize that the wave is a wave. |
The moderately reductionist viewpoint is sometimes useful but sometimes not. No matter what viewpoint you take, the wave has properties that transcend its embodiment in a particular medium. Over on one side of the room the wave is a bunch of rope-particles moving up and down. Then it propagates over to the other side of the room and becomes a bunch of chain-particles moving up and down. However, we still recognize it as the same wave. The wave is the same, even though the medium has changed. Most (but not all) properties of the medium are completely different.
Furthermore, the wave propagates from left to right, even though the medium does not move from left to right. The medium ends up exactly where it started. We can talk about the velocity of the wave, even though no part of the medium is moving with that velocity except possibly by accident. The wave is an abstraction. The wave has properties of its own, separate from the properties of the medium.
We can continue the reductionist process quite a ways, step after step. The wave is made of rope, the rope is made of organic molecules, the molecules are made of atoms, the atoms are made of subatomic particles, and so forth.
Saying there is no such thing as a wave is just a silly as saying there is no such thing as a rope. The reductionist viewpoint is sometimes helpful as a way of looking at things – but it is not the only way of looking at things.
You can take the reductionist viewpoint if and when you like. On the other hand, you would be tragically limiting yourself if that were the only viewpoint you were able to take. You are free to choose whatever viewpoint(s) you like, but remember that other folks are free to choose differently.
In section 3.2 we moved from big to small: The wave is made of rope, and the rope is made of atoms, et cetera.
We can also analyze things the other way around: Starting with atoms, we can put atoms together to make a rope. Continuing from there, we can consider waves on the rope.
In particular, consider the wave shown in figure 3. It is diagrammed in figure 5. The wave is an organized, collective motion of the atoms. The wave has some collective properties, such as its shape and its energy, that remain more-or-less constant as it propagates along. The wave is not a property of any individual atom by itself, but rather a an emergent property, i.e. a property of all the atoms collectively.
Any given piece of rope can support multiple waves at the same time: some wiggles here, some wiggles there, some propagating in different directions. Mathematically, this is represented as a field. We say any such wave is an excitation of the field.
I mention this because sometimes people try to argue that tangible material things like electrons, atoms, and ropes are real, but waves are not real; the wave is (allegedly) “just” an abstract collective motion of the rope. Well, that is just completely wrong physics. In reality, according to any modern understanding of physics, the electron itself is a quantized excitation of a certain field ... just as the wave in figure 5 is an excitation of the rope’s displacement field. Waves exist at both the top and the bottom of the constructive/reductive hierarchy, as shown in figure 6. If you don’t think waves are real, then nothing is real.
A great deal of physics is representational. We build models that represent the physics. The representation may involve some combination of equations, pictures, computer programs, tangible mechanical models, et cetera. The question is not whether or not to build models; we are going to build models. The only questions are to what extent this-or-that model is convenient, and to what extent it is faithful to the underlying reality.
I am using the word “real” as the antonym of “fictional”. (All my dictionaries approve this usage.)
Abstract is the opposite of concrete; it is not the opposite of real. The relationships are spelled out in figure 7.
To my way of looking at it, waves are real. I don’t care whether the waves are tangible or even visible; the important point is that waves are created, propagated, and destroyed according to strict natural laws. Ropes are also real. Of course they can be created from scratch, they can be destroyed, and they can behave in complicated ways – but only according to natural laws. The same goes for energy, as discussed in section 5.1. Energy is just as real as waves, and as real as ropes. Energy may be intangible and almost invisible, but it obeys laws that are simple, strict, and very well understood.
Many of the central, crucial laws of physics deal with abstractions. Examples include:
As a simple example, consider the energy in the wave in figure 5. The energy flows from left to right, even though the rope does not. Even though energy is an abstraction (as discussed in section 5.1), and flow is an abstraction (as discussed in section 5.3), the laws of physics give us some interesting information about such things, some very definite, important information.
Another example concerns electrical charge. This is definitely an abstraction. As discussed in section 5.4, tangible, material particles are not conserved, but the abstraction – charge itself – is conserved. If you focus on the tangible, material things, you are going to miss the important fundamental physics.
There are two ways of looking at the situation, as you can see by comparing figure 8 with figure 9.
As indicated in figure 8, we could think of a “wave on a rope” and a “wave on a chain” as being two separate things. However, as indicated in figure 9, life is simpler if we introduce a layer of abstraction. We think of a single wave carried by a single medium, even though part of the medium is made of rope and part of the medium is made of chain.
Let’s be clear: This abstraction makes things simpler. It reduces the number of things you need to learn. It means you do not need to worry about the details of the substances that make up the medium. You are allowed to look into the details, but you are not required to.
As another way of saying the same thing, the idea of a “wave on a medium” is a generalization of the ideas of “wave on a rope” and “wave on a chain”. The more-general idea is more powerful and more useful.
People are really good at this sort of thing. Consider a four-year-old child playing with a baby doll. Everybody knows it’s not a real baby; it is a symbol that represents a baby.
The most elementary idea of counting depends on this sort of generalization and abstraction. You start with the idea of four cows, four pots, or four chairs ... and then generalize to the idea of four itself, i.e. the idea of four abstract things. Four pots is different from four chairs in some important ways, but it is also the same in some important ways.
In high-school geometry, the central concepts – such as points, lines, and planes – are explicitly defined to be completely abstract. (They approximately correspond to certain properties of the real world, but to a mathematician that is irrelevant.)
In physics, many of the most fundamental concepts are completely abstract. This includes energy, momentum, and electric charge, among other things.
Here’s another thing we can learn with the help of figure 9: The wave is on a different plane of existence from the medium. Although the wave cannot exist without the medium, the behavior of the wave is different from the behavior of the medium. Specifically:
| The medium wiggles north/south as the wave passes, and then returns to its initial state. | The wave flows from west to east and never returns. |
The terminology of a “different plane of existence” comes from eastern mysticism, but there is nothing mystical about what we are saying about waves. This is hard-core quantitative physics.
There are many forms of energy. Sometimes it is embodied in the gravitational potential energy of objects. Sometimes it is embodied in the kinetic energy of objects. Sometimes it is embodied in electromagnetic radiation. However, as far as we know, energy never exists in isolation; it cannot exist separately from some sort of embodiment.
Still, energy has important properties that transcend any particular embodiment. Just as a wave in figure 5 can propagate from the rope to the chain and still be recognized as the same wave, energy can flow from the rope to the chain and still be recognized as the same energy. As another way of visualizing the same thing, consider figure 10. (Video courtesy of GiantNewtonsCradle.com.) Initially there is some energy in ball #1. The energy then flows through ball #2, ball #3, and ball #4 without accumulating there. It accumulates in ball #5, which goes flying.
The net effect is that energy has flowed out of ball #1 and flowed into ball #5. Even though the energy is embodied in a completely different ball, we recognize it as the same energy.
Some people loudly insist that energy is not a “thing”. That indicates a remarkable non-understanding of what energy is, and/or what a thing is. Energy is an abstract thing. It is not a tangible material thing, but it is still a real thing.
My opinion is supported by my dictionary (Random House) which gives 21 definitions for the word “thing”. Of these, items 3, 4, 5, 6, 7, 8, 11, 13, 15, 16, 18, 19, 20, and 21 clearly refer to abstract and/or intangible things.
Saying that energy cannot be a “thing” is beyond pedantry – it’s just plain wrong.
Chief among the properties that we ascribe to energy per se is the local conservation law. That is: Energy cannot be created or destroyed. Any decrease in the amount of energy in a given region must be balanced by a simultaneous increase in the amount of energy in an adjacent region. (For details on this, see section 5.3 and reference 2.)
Saying that energy isn’t “real” is like saying that waves don’t really exist, or like saying that rope doesn’t really exist.
Momentum is an abstraction, for all the same reasons that energy is an abstraction. Indeed, special relativity tells us that energy and momentum are intimately related. They are the components of a single four-dimensional vector. For details on this, see reference 3.
In particular, it would be a mistake to restrict your definition of momentum to the motion of tangible material particles. There is also momentum in the electromagnetic field.
It would be a mistake to define “flow” in terms of the mechanical motion of tangible objects. We need a more sophisticated, abstract notion of flow.
Definition: Consider some quantity X, which could represent something tangible like water, or something more abstract like energy. Suppose a certain amount of X disappears from one region of space, and simultaneously the identical amount of X appears in an adjacent region. We can safely say that X flowed from one region to the other.
This notion of flow is more inclusive. It works just fine for the flow of water, and it also works for the flow of charge, energy, and other abstract quantities.
For more about conservation in terms of continuity of flow, see reference 2.
Let’s talk about conservation of charge. Charge is not primarily about concrete tangible things. It is much more abstract than that. We can illustrate this point in multiple ways.
For starters, note that when the charge in a particular region increases, it does not mean that a positively-charged particle moved into the region. It could equally well mean that a negatively-charged particle moved out. The increase in charge is the same either way.
A specific example is shown in figure 11. Suppose we have an electrochemical cell. In the left part of the cell, sodium ions are flowing left-to-right. At some point the sodium ion bumps into a previously-stationary potassium ion. The sodium ion stops moving, and the potassium ion starts moving.
Recall that in figure 5, the wave moved from the rope to the chain, but we recognize it as being the same wave. Different substance, same wave. The situation in figure 11 is closely analogous. The left side and the right side have different chemistry, but we recognize the charge as being the same. Electric charge is completely abstract. The laws of electromagnetism do not care about the chemistry; they only care about the charge ... or more specifically, the [charge, current] four-vector.
Here’s another example along the same lines: A pion is a type of subatomic particle. One type of pion is negatively charged, in the same way that an electron is negatively charged. Now, as shown in figure 12, suppose such a pion (π−) flows into a box. While it is there, it decays into a negatively-charged muon (µ−). A short time later, the muon decays into an electron (e−). (There are other particles involved in these decays, notably neutrinos, but they are all uncharged, so they do not affect the charge-conservation story.)
This can be summarized in an interesting way:
The lesson here is that if you focus on the tangible, material things, you are going to miss the important fundamental physics. Pions, muons, and electrons are tangible, material things, but they are not entirely well behaved. Electrical charge is an abstraction, and is much better behaved.
Here’s another argument leading to the same conclusion: If you have a bunch of electrons flowing left-to-right, it means charge is flowing right-to-left. That’s because electrons are negatively charged. So, once again we see that charge is an abstraction. The laws of electromagnetism have a lot to say about this abstract charge, and very little to say about whatever tangible particle(s) might be carrying the charge.
So, once again we see that (a) charge is an abstraction, and (b) our notion of flow is an abstraction, more subtle and more powerful than the mere motion of tangible particles. The sooner you make friends with abstractions such as energy, charge, et cetera – accepting them as abstractions – the better off you will be.
As mentioned in section 4, electric field lines are sometimes used to model the electric field vector. Like all models, they have some advantages and some advantages. They are in some ways an apt representation, and in some ways not.
What’s more interesting is that the thing the field lines are trying to represent, namely electric field vector, is itself a model, and it is not best available representation of the underlying physics! The E-vector is notoriously not relativistically covariant. It is not even part of any useful 4-vector.
The clever way to represent the electromagnetic field is as a bivector. This bivector is relativistically covariant, which means that if you draw a picture of it, everybody (in every reference frame) agrees that is the right picture. This is in dramatic contrast to electric field lines, which different observers would draw differently.
Almost all the usual objections to “field lines” can be removed if you build a model of the electromagnetic field bivector (rather than the electric and/or magnetic field vectors). Yeah, I know drawing bivector fields is harder than drawing lines, but it’s not impossible. A number of good examples can be found in reference 4. Some more modest examples can be found in reference 5 and reference 6.
You are going to need some chain and some rope with the same mass per unit length. Discrepancies of 20 or 30 percent in the mass per unit length won’t matter much; just do the best you can.
Splice one end of the rope to one end of the chain, to make a combination that is half rope and half chain. Have two assistants hold the ends of the combination, or better yet, fasten the ends to suitable supports. Don’t make it unreasonably tight, just tight enough that it doesn’t drag on the floor or other obstacles.