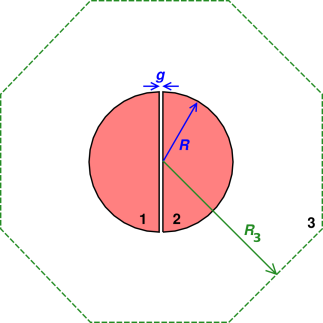
Figure 1: 3-Terminal Spherical Capacitor
Suppose we have N objects, each of which is a piece of conductive material. The ith object has voltage Vi and carries charge Qi
We are going to assume that if we have some charge in a certain equilibrium arrangement, we can (say) double the amount of charge and the charges won’t move; that is, the double-charge arrangement will also be in equilibrium. This is not true in general, for instance if varactors or other lightly-doped semiconductors are involved, or if the electrodes are free to move (as in a gold-leaf electroscope) … but it is a reasonable approximation for immovable metal electrodes.
Based on this assumption, and on the linearity of the basic equations of electrostatics, we expect that there will be a linear relationship between the charge variables and the voltage variables. We write this relationship as:
| Qi = Cij Vj (1) |
where Cij is called the capacitance matrix. This defines what we mean by capacitance.
Let’s consider the simple case where there are only two conductors. They could be, for example, the two plates of an ideal parallel-plate capacitor. For reasons that will be explained later, the full capacitance matrix must have the form:
| C = | ⎡ ⎢ ⎣ |
| ⎤ ⎥ ⎦ | (2) |
In order to make manifest the symmetries of the situation, we define the differential-mode voltage
| ΔV := V2 − V1 (3) |
and the common-mode voltage
| Vc := V2 + V1 (4) |
Inverting these relationships we find
| (5) |
Then we just do the algebra:
| (6) |
So, what have we learned?
For starters, we observe that for each of the two plates, the charge depends only on the differential voltage ΔV and is independent of the common-mode voltage Vc. This is an example of gauge invariance, as discussed in section 1.4
Secondly, we observe that the charge on the first capacitor plate is equal and opposite to the charge on the second capacitor plate. This is a consequence of global charge neutrality, and of the fact that there are no other objects in the universe. Whatever charge appears on object #1 must have been taken from object #2 and vice versa. See section 1.4 for more on this.
Thirdly, as a consequence of these two fundamental physical principles (gauge invariance and charge conservation), as soon as you know one matrix element in a 2×2 capacitance matrix, you know all the others. It’s the world’s easiest sudoku puzzle.
Important caveat: The simple analysis in this section only applies when the two objects have equal and opposite charge. If you are interested in the case of two objects with unbalanced charge, you need to treat it as a 3×3 problem, as discusses in section 1.5.
Terminology: For a two-terminal capacitor, the matrix element b is conventionally called “the” capacitance of the capacitor. It is conventionally denoted C or c. Here we have been calling it b just to avoid confusion with the full capacitance matrix C.
In the case of a parallel-plate capacitor, where the plate area is A and the gap between the plates is g, we have
| b = |
| (7) |
assuming the gap is small compared to the smallest dimension of the plates.
In the case of concentric spheres, we have
| (8) |
Dubious terminology: The first line of equation 8 is commonly called the mutual capacitance of the two spheres. In contrast, the second line of the equation is commonly called the self capacitance of the R1 sphere.
Dubious concepts: As far as I can tell, there is no good physical basis for distinguishing self capacitance from mutual capacitance; the so-called self capacitance of an object can perfectly well be considered the mutual capacitance between that object and the surroundings. If the surroundings are far away, the details of the surroundings may not matter much, but at some conceptual level the surroundings are always important. You are free to choose the potential of the surroundings (the chassis or whatever) to be zero, by exercise of gauge freedom, but keep in mind that others may choose differently.
Any capacitance matrix must have the following properties:
You can verify that the examples in this section (equation 2 and equation 14) satisfy these requirements.
Let’s turn our attention to the situation shown in figure 1. Object #1 and object #2 are hemispheres of radius R separated by a gap of size g. They are enclosed by a Faraday cage (object #3), represented by an octagon drawn with a dashed line. The size of the cage is huge compared to R, and R is huge compared to the gap g.
We are going to treat this as a three-terminal device. That is, we are going to explicitly account for the charge and voltage on each of the three objects.
To capture the symmetry of the situation, we express the voltages in terms of the following three numbers: V3, Vs, and Va. The mnemonic is s stands for spherically symmetric and a stands for antisymmetric. The meaning of these numbers is defined as follows:
| (9) |
Inverting equation 9 we find
| (10) |
If Vs is zero, then the two hemispheres behave as a parallel-plate capacitor, with
| (11) |
which is independent of V3.
If Va is zero, then we have just a spherical capacitor, with
| (12) |
which is again independent of V3.
Given these expressions for the charges in terms of the voltages, there is a straightforward procedure for finding all the matrix elements of the capacitance matrix. The trick is to differentiate the definition, equation 1. That gives us:
| Cij = dQi / dVj holding all Vk constant except Vj (13) |
Using that trick, we find that the capacitance matrix takes the form
| C = | ⎡ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎦ | (14) |
where x = є0πR and y = є0πR2/g.
It is even easier to verify equation 14 that it was to derive it. Just plug in some example values for the three voltages and see how the charges work out.
You can use these spreadsheets to calculate capacitance. The basic idea is to use equation 13, or rather a discrete approximation thereto.
We start by assigning suitable voltages to objects on the potential-grid and observing the induced charges. We find the total charge on each object by summing the cells of the charge-grid occupied by each object.
Then we hold N−1 of the objects at constant potential and wiggle the voltage on the remaining one. We observe what happens to the charge on each and every object by turning the crank on Laplace’s equation. This gives us numerical values for the partial derivatives in equation 13, and therefore numerical values for the matrix elements Cij.
A spreadsheet for solving Laplace’s equation for arbitrary 2-dimensional geometries is discussed in reference 1.
The full capacitance matrix Cij gives the charge as a function of voltage, in accordance with equation 1. Alas, this function cannot be inverted to find the voltage distribution as a function of the charge distribution. The matrix is singular. Charge conservation guarantees that it is singular. Gauge invariance also guarantees that it is singular.
The task of finding the N voltages as a function of the N charges is ill-posed. First of all, we only need N−1 of the charges (because we can always infer the Nth charge, using global charge neutrality). Secondly, if we have a solution for the voltage distribution, we can always find another solution by a gauge transformation: adding a constant to all of the voltages. So we can summarize the situation by saying that the N voltages are determined by N−1 charges and one gauge.
Operationally, to find the voltages as a function of the charges, the procedure is as follows: Form a diminished capacitance matrix by dropping one row and one column of the full capacitance matrix. Dropping a column corresponds to setting one of the voltages to zero. We can always do this, by fiat, by exercise of gauge invariance. Dropping a row means we are considering the charge on one of the objects to be a dependent variable, implied by the remaining N−1 independent charges.
You can choose to drop any one row and any one column. They need not intersect at the diagonal.