Figure 1: Energy Flow – Three Scenarios
Question: For a gas in a cylinder with volume V, pressure P, and energy E, would you agree with the following equation?
| P = − |
| ??? (1) |
Answer: The RHS is horribly ambiguous. In the case of a monatomic ideal gas, possibilities include:
| − |
| ⎪ ⎪ ⎪ ⎪ |
| = 1.5 P (2) |
| − |
| ⎪ ⎪ ⎪ ⎪ |
| = P (3) |
| − |
| ⎪ ⎪ ⎪ ⎪ |
| = 0 (4) |
Lesson: A partial derivative is not much more or less than a
directional derivative. When writing a partial derivative,
always indicate the direction.
For details on the correct definition of pressure, see reference 1.
Suppose our “system” consists of some gas in a cylinder with a piston. External to the system, a spring pushes on the cylinder. In the familiar adiabatic case, we can use the principle of virtual work to understand how the gas pressure opposes the force of the spring. Equation 3 is a straightforward application of PVW.
Recently I was asked about equation 4. It was alleged that:
In analogy to equation 3, if the gas was in sufficiently intimate contact with a heat sink, if the piston moved inward a little bit, the energy of the gas would be unchanged. By PVW, that would mean the gas was exerting no force on the piston. The spring would crush the gas to very high density. The rate of crushing would be limited mainly by how fast the heat sink could do its job.
That seemed like a paradox. Thermodynamic equations were allegedly saying something that common sense said couldn’t possibly be true.
Disclaimer: Something in the indented paragraph isn’t true. Normally I abhor saying things that aren’t true. I think discussing paradoxes is a poor pedagogical technique, especially in introductory courses. (Yes, this includes all those infamous relativity paradoxes.) I especially abhor contrived paradoxes ... but this one wasn’t contrived; it came to me fair and square.
Usually the best way to proceed is to learn to formulate problems sufficiently clearly that paradoxes cannot arise. The following section presents a good way to formulate and analyze the isothermal pressure problem.
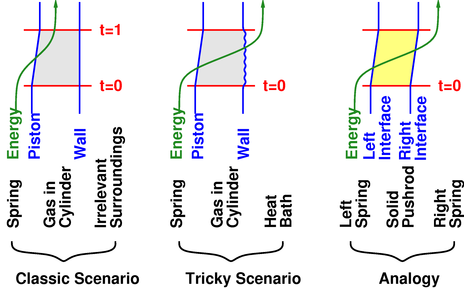
Please refer to figure 1. There are three space-time diagrams, representing three slightly different scenarios. In each scenario, the green line is the world line of a parcel of energy.
In the classic scenario, we see that during the time period from t=0 to t=1, the piston moves inward slightly, as indicated by the change in position of the piston’s world line (shown in blue). The gas is compressed adiabatically. Some energy is transferred out of the spring and into the gas. In this scenario, the energy remains in the gas.
In the tricky scenario, things are pretty much the same, except that the compression is isothermal, not adiabatic. The energy that is transferred out of the spring does not remain in the gas, but is passed on into the heat sink.
From this we can see that the isothermal pressure is the same as the familiar “classic” pressure. That’s because from the point of view of the piston, the energy flow is the same. The same amount of energy flows through the piston.
To say the same thing another way, the principle of virtual work is conventionally written
| F = − ∇ E (5) |
but (!) the E that appears in equation 3 represents only the energy of the system, while the E in equation 5 represents something else – in this case, the energy of the system and the heat sink together.
The third scenario is an analogy that makes this point even more clear. We replace the gas-cylinder with a solid pushrod. The spring on the left wants to push the rod leftward, but we have arranged for another spring on the right to push rightward, establishing equilibrium. Applying PVW to this situation, it would be silly to use the E of the pushrod alone; we know that energy flows through the rod, and PVW must be applied to the energy of the rod and spring together.
In modern physics it has been found helpful to express all the laws as local laws. That is, what is going on at one point in space depends only on the neighborhood of that point, not on any far-away points.
In the section 1.3, we saw that the E appearing in equation 5 should be interpreted as the energy of the gas and the heat sink together. That seems like a violation of the idea of locality. The piston is in contact with the gas, but not the heat sink ... so it seems disturbing to think that the force on the piston depends on the energy of the far-away heat sink.
The right way to proceed is not to make PVW less local, but rather to make it more local! The force on the piston does not really depend on variations in the energy of the gas, or the energy of the heat sink ... it depends on the energy flow through the piston. Once the energy has flowed through the piston, we don’t care whether it stays in the gas or not.
The really, really local phenomenon is energy flow through the piston.
Another lesson concerns the term “work”. This is, alas, a somewhat shifty concept.
In mechanics, there is a work / kinetic energy theorem, which is indeed a theorem. So far so good.
The first problem is, kinetic energy is not (by itself) conserved, and therefore work is not (by itself) conserved. This makes it hard to keep track of the work.
A second problem, arguably even more serious, is that thermodynamics books use the term work to apply only to macroscopic work ... which is related to macroscopic kinetic energy, not including any microscopic forms of energy. (For details on macroscopic versus microscopic kinetic energy, see reference 2.)
Combining the two previous ideas, we find that macroscopic kinetic energy can be converted to macroscopic potential energy and/or converted to microscopic forms of energy (including microscopic potential energy as well as kinetic energy).
Therefore you should not think that the “work” in the principle of virtual work is the same “work” that is discussed in thermo books.
The thermodynamic notion of “work” is almost as widely abused as the thermodynamic notion of “heat”.