Odometers and Clocks in Introductory Relativity

Abstract:

The geometric approach to special relativity emphasizes the proper length (as measured by odometers) and the proper time as (measured by ordinary clocks). These properties are intrinsic to the odometers and clocks, unaffected by the motion of this-or-that reference frame.

The geometric approach treats space and time on the same footing, and treats rotations and boosts on the same footing. As a consequence we see an ordinary clock as being more similar to an odometer than to a rigid ruler.

Relativity should not be considered weird or paradoxical; it is just the geometry of spacetime. A good qualitative understanding of the essential ideas can be achieved just by using diagrams to show the correspondence between spacetime and ordinary space. This does not require much beyond high-school notions of geometry, trigonometry, and vectors.

The geometric approach stands in contrast to the so-called contraction/dilation approach, which alleges that rulers contract (relative to lab-frame rulers) and clocks run more slowly (relative to lab-frame clocks) when moving (relative to the lab frame). The geometric approach has so many advantages – in terms of simplicity, power, elegance, modernity, and consistency – that one wonders why anybody would bother with the other approach.

Additional keywords: intrinsic length, invariant length, invariant mass, chord length, chord time, inertial navigation system, twin “paradox”, FitzGerald-Lorentz contraction, time dilation, time dilatation.

1  Preliminaries

Note: If you are learning about relativity for the first time, please do not start here. Please read reference 1 (“Welcome to Spacetime”) before reading this document.

The following must be one of the most profound sentences in human history:

We will make heavy use of this idea, namely the idea of spacetime. Time is the fourth dimension. Time is slightly different from the other three dimensions, but it is more the same than different. Relativity is nothing more – or less – than the geometry and trigonometry of spactime.

We shall see that this one simple idea has a huge range of profound consequences, as you can see in the right-hand column of the following list:

Any one of the ideas in the right-hand column would be interesting. Any two of them would be an amazing coincidence. The whole package is beyond amazing. It beggars description.

As you can see from the color-coding, at least half of what relativity tells us is stuff we already knew. Many relativistic ideas have been known for centuries under other names, and are merely unified and systematized by relativity. Therefore you should not think that relativity is weird. Most of it is quite prosaic. You could make it seem weird if you disregarded the familiar parts and overemphasized the unfamiliar parts ... but that would be unfair and unwise, so let’s not do that.

We should also say a few words about general relativity:

A good introduction to spacetime can be found in reference 3. Another discussion of the correspondence between xy rotations and xt rotations can be found in reference 4.

Terminology: In this article, the term “vector” will always refer to a physical vector, which is a physical object unto itself, existing in space or spacetime. This is in contrast to any notion of a vector being defined as a list of components. If you switch from one reference frame to another, the physical vector stays the same, but the components change, as discussed in reference 5.

Terminology: The word proper as used here, in expressions such as “proper time” and “proper length”, means “its very own”, as in “proprietary”. (Other meanings of “proper”, e.g. “correct” or “appropriate”, are not relevant here.)

2  Proper Length

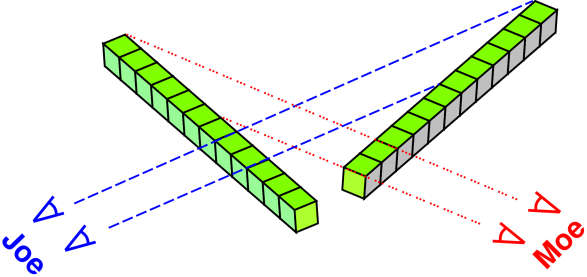
To understand what we mean by proper length, consider figure 1. It shows two rulers, each 12 inches long.

This example involves only ordinary Euclidean geometry; the analogy to relativity will become apparent soon.

Figure 1: Foreshortening

The foreshortening is symmetrical, in the sense that Joe sees a foreshortened projection of Moe’s ruler, while Moe sees a foreshortened projection of Joe’s ruler.

The point here is that ordinary rulers have a well-understood property we call length. When we view a ruler somewhat end-on, we do not conventionally say that its length has changed. We might say that the ruler appears foreshortened, or that the projection of the ruler onto our field of view is foreshortened … but “the” length is an intrinsic property of the ruler, and is invariant with respect to rotations.

We now wish to show the correspondence between ordinary geometry (typeset on the left side of the page) and relativity (typeset on the right side of the page). One might be tempted to assume that foreshortening is analogous to the FitzGerald-Lorentz contraction, but we have to be careful, because that idea is “mostly correct” but not entirely correct, as we shall see.

Figure 2: FitzGerald-Lorentz Contraction

Note: We are talking about a sophisticated sort of snapshot here. Joe makes use of a whole array of assistants, spread out along a contour of constant time in Joe’s frame. They answer questions about events in spacetime: Is there a piece of stick at your location right now? This sophisticated snapshot is immune from the Penrose-Terrell aberration that would plague pictures taken with a simple box camera.

At present, it is all-too-common for “popular’ accounts of relativity to suggest that the snapshot length, i.e. the FitzGerald-Lorentz-contracted length, should be considered “the” length of the stick. The same goes for introductory-level textbooks. However, we predict that over time, this will change, so that the proper length will come to be considered “the” length. This situation is analogous to the earlier shift in the meaning of “the” mass.

In relativity, there are at least three different notions that can be used to describe vectors:

a) The vector itself, considered as a geometric object in spacetime, existing independently from any observer and from any reference frame. (See reference 5.) The vector’s proper length (but not its direction) is independent of the choice of reference frame.

b) The components of the vector, in some given reference frame.

c) The snapshot length, i.e. the FitzGerald-Lorentz contracted length, which extends along the x direction in a given reference frame, but is not actually equal to the x component of the vector.

3  Projections versus Dejections

All projections considered in this article are orthogonal projections, whether or not we explicitly call them orthogonal.

The rule for making an orthogonal projection is as follows: to project an object onto a given axis, carry each point of the object along a contour truly perpendicular to the axis, until it reaches the axis.

Applying this rule correctly is slightly tricky on a spacetime diagram, because the geometry of the diagram-on-paper is not an entirely faithful representation of the true geometry of spacetime, as discussed in reference 4. Things that are truly perpendicular in spacetime may not look perpendicular on the diagram. For example, if you want to project something onto Moe’s x-axis (a red broken line in figure 2) you need to carry points along Moe’s contours of constant x (red solid lines in figure 2). On the right side of the diagram, they don’t look perpendicular on paper, but they are truly perpendicular in spacetime.

Specifically, if we project the heavy green bar onto Moe’s x-axis, the result corresponds to the black arrow. The reverse is not true; the heavy green bar is not the projection of the black arrow onto Joe’s x-axis. Instead we call the heavy green bar the dejection of the black arrow. (Logically and lexically this should probably be called the rejection, but mathematicians have already given that word a different geometrical meaning.)

4  Reality versus Appearance

We do not wish to have a philosophical debate about which notion of length is “real” or “correct”. It is better to ask which notions are useful under what conditions. Someone who has truly mastered the subject should be able to see things from more than one point of view, switching back and forth when necessary.

It would be unwise to accept things as “real” if and only if they can be directly measured. That’s because appearances can be deceiving. Oftentimes the important quantities can only be measured indirectly.

This point can be nicely illustrated using figure 3. This is a photograph of Saturn. The image is “real” in the sense that it is not a fake or an artist’s conception. The image of the rings is highly elliptical; specifically, the major axis is about six times as long as the minor axis. This is what our direct measurements are telling us.

Figure 3: Image of Saturn ./img48saturn.jpg

Meanwhile we would say that in “real” space, the “real” rings are very nearly circular. The pronounced eccentricity of the image is a property of the image, not a property of the “real” rings. In particular the eccentricity is a property of the projection that occurred when the image was made, not a property of the “real” rings.

5  Intrinsic versus Projective

Let us consider the notorious “pole in a barn” problem that crops up in many textbook discussions of relativity. The scenario calls for a pole-vaulter carrying a pole, running at relativistic speed through a barn. The proper length of the pole is equal to the proper length of the barn. The textbook alleges that in the frame of the barn, “the” length of the pole is Fitzgerald-Lorentz contracted, so that the pole definitely fits inside the barn ... whereas in the frame of the runner, the textbook alleges that the barn is contracted, so that the pole definitely does not fit.

It is amusing to compare the pole-and-barn system to the Saturn ring system (figure 3). In each system, there is a masochistic way and a sensible way to describe what is happening.

We mention this because – hitherto – people have not sufficiently appreciated the importance of intrinsic properties (as opposed to projective properties) when discussing the pole-and-barn, the skateboard-and-manhole, and a host of similar problems.

In summary, there are rather strong reasons why it is usually advantageous to focus attention on intrinsic properties such as proper time and proper length.

• The invariance of length with respect to boosts is consistent with the well-established invariance of length with respect to rotations.
• It allows the physics to be expressed more simply.
• Students can use their intuition about ordinary geometry to understand special relativity, and even general relativity.
• Conversely, exposure to spacetime and four-dimensional vectors reinforces and deepens students’ understanding of ordinary geometry and three-dimensional vectors.

6  Traveling Twins

We now use what we know about length to help us understand time.

We start with a variation on the story of the notorious twins, Joe and Moe. They travel from event A to event D, each in his own car. Each car is equipped with an odometer and a clock. All the clocks and odometers are set to zero at the start of the trip.

6.1  Odometer-Distance versus Chord-Distance

At the end of the journey, Moe’s odometer shows a greater reading than Joe’s. There are two contrasting ways of explaining this result.

a) It could be that Moe’s odometer is faulty, and records some weird “contracted” units of distance.

b) A far simpler explanation is that both odometers are functioning correctly, and that Moe took the scenic route, while Joe took the direct route.

Explanation (b) is familiar to us, in our non-relativistic travels through ordinary Euclidean space. Some paths are longer than others. Some instruments (notably rulers) are meant to be rigid, so that they measure the invariant distance between A and D. Meanwhile, other instruments (notably odometers) are meant to measure the path-length. Other instruments (notably measuring tapes) can be used either way.

Figure 4: Odometer versus Ruler

The distinction is portrayed in figure 4. Joe takes the direct path from A to D, so he can measure the length using a rigid ruler. Meanwhile, Moe takes the scenic route. The distance that he travels can be measured by an odometer, or equivalently by a flexible measuring tape that conforms to his path ABD.

As a useful bit of terminology, everyone (including Moe) can say that the ruler in figure 4 measures the chord length, i.e. the length of the chord drawn from point A to point D. Chord length stands in contrast to the proper length of Moe’s path ABD, aka the arc length. Chord length is equal to path length if and only if the path is straight; this effectively defines what we mean by “straight”.

6.2  Clock-Time versus Chord-Time

The story of the traveling twins becomes even more interesting when we look at the clocks. Moe’s clock shows less elapsed time than Joe’s.

a) It could be that Moe’s clock is faulty, and records some weird “dilated” units of time.

b) A far simpler explanation is that both clocks are functioning correctly, and that Moe took the scenic route through spacetime, while Joe took the direct route.

In the remainder of this section, we adopt description (b). We are not suggesting that description (a) is wrong; we just find description (b) vastly more convenient and more elegant.

In spacetime, clock readings are path-dependent for the same reason that odometer readings are path-dependent.

The geometry of spacetime (reference 4) is such that the scenic route will always rack up more mileage and less elapsed time than the direct route. [In some sense this defines what we mean by the direct route. This is related to the principle of least time (in geometrical optics) and the method of stationary phase (in wave mechanics and quantum mechanics), but details are beyond the scope of this article.]

This description has the virtue of consistency. In spacetime, we find it convenient to treat time on the same footing as space, and we find it convenient to treat boosts on the same footing as rotations. (reference 4) Just as viewing a ruler end-on does not change “the” length, viewing a fast-moving clock does not change “the” time between clock-ticks. The projection onto our frame of reference may be foreshortened or dilated, but this is just a property of the projection, not a property of the rulers or clocks themselves.

Naive nonrelativistic experience suggests that the elapsed time between event A and event D is independent of the path. This is true in the non-relativistic limit, but it is not true in general. We can say the same thing more graphically, using a spacetime diagram: elapsed time is path-independent if all reference frames are moving along parallel world-lines, but not if the frames’ world-lines are angled relative to each other. If relativistic speeds are involved, elapsed time is path-dependent in the same way that odometer readings are path-dependent.

Many textbooks put forth an argument of the following form: “Moe’s clock racks up less elapsed time, therefore it must have been running more slowly.” This argument is invalid, since it is based on the false assumption that the correct elapsed time would be path-independent.

Let’s be clear: Yes, at the end of the journey, Moe is younger than Joe (assuming they started out with equal ages). No, this does not prove that Moe’s clock ran slower. A far simpler explanation is that Moe took a less time-consuming path.

Another line of argument starts by considering events called clock ticks. Each tick is an event in the technical sense of the word, meaning it occurs at a definite place and a definite time in spacetime. We take it as the defining property of a well-behaved clock that it produces clock-ticks at a uniform rate, according to the contours of constant time in a reference frame at rest with respect to the clock. This definition certainly upholds the correspondence principle.

A set of such clock-ticks is indicated by the red circles in figure 2, near the left edge of the spacetime diagram. These were produced by a clock at rest in Moe’s frame.

The usual argument asks us to calculate

where τ is Moe’s proper time, t is the time in Joe’s reference frame, and ρ is once again the rapidity, namely the rapidity with which Moe’s frame is moving relative to Joe’s frame.

You can calculate Δt/Δτ geometrically using figure 2, as follows: As Moe travels from one red circle to the next, his clock ticks off one unit of “red” time, so Δτ = 1. Meanwhile, the projection of the vector onto Joe’s t axis is 13% longer than that. That is, Joe must wait more than one unit of “blue” time between the same two events.

You can also calculate Δt/Δτ algebraically.

Whether you do it geometrically and/or algebraically, everybody agrees on how to do this calculation, and everybody agrees on the numerical answer. However, all-too-often the result is encrusted with layers of metaphysics and questionable interpretations. In particular, intro-level textbooks commonly conclude from this that Moe’s clock is running slower … but any such conclusion is highly questionable. A far simpler interpretation is that Moe’s clock is keeping time just as it should, and that Δt/Δτ merely describes the projection from Moe’s frame onto Joe’s frame.

The ratio Δt/Δτ is a property of the projection, not a property of anybody’s clock. In particular, it is an orthogonal projection (like the rings in figure 3), not a dejection (like the heavy green bars in figure 2). As mentioned in section 3, projections have the property that a foreshortened ruler always appears shorter than its proper length, while the time between ticks of a moving clock always appears longer than the proper time.

In analogy to chord length, we can define a notion of chord time, namely the time ticked off by a clock that moves from point A to point D along an unaccelerated world line, i.e. a straight line on the spacetime diagram. We coin the name chordochronometer for an instrument that measures this quantity. Chord time is equal to proper time if and only if the path is unaccelerated. Reference 6 gives some formulas for calculating chord time.

The notion of “the” spacetime interval is widely used in the literature, but is ambiguous. We prefer to speak of the chord length and chord time, for reasons discussed in reference 4.

6.3  “Natural” Notions of Distance and Time

We emphasize that ruler distance and odometer distance are two well-defined, useful concepts … they just don’t happen to be the same concept. Each has a frame-independent definition (unlike Lorentz-contracted length, which pertains to a particular reference frame).

The relationship between ruler distance and odometer distance can be clearly seen if we consider a trip consisting of many steps. Let the ith step be described by a short vector, s_i. Then we have:

That is, the only difference is whether you sum before you take the norm, or take the norm before you sum. It would be silly to suggest that either of these is more “real” or more “physical” than the other. They both make sense; they’re just different.

The most complete and most “physical” description of the path is to specify all the short vectors, s_i. Each such vector is local to the path, intrinsic to the path, presumably directly measurable, and independent of the choice of reference frame. Given the entire sequence (s₁, s₂, ⋯), you have a complete description of the path. From there, you can summarize the data in various ways (ruler distance and/or odometer distance and/or whatever). Any such summary gives a less-than-complete description.

As you travel along your path, you are permitted to keep a running estimate of the ruler distance and/or odometer distance … but you are not required to.

The ruler distance has the nice simplifying property that it depends only on the endpoints of the path. It is just the ordinary distance between the endpoints, which can be calculated without knowing any other details of the path.

It is straightforward to build an odometer for a wheeled vehicle; you don’t need to do much more than count the revolutions of a wheel. It is a more challenging – conceptually as well as technically – to keep track of path length and/or chord length along an arbitrary path through spacetime. The usual name for a device that does this is inertial navigation system (INS). An INS needs one brief peek at an external reference, so it can know its initial position and initial velocity, but thereafter it does not depend on external references.

An INS can be concisely described by saying it finds the velocity by integrating the acceleration, and then finds the position by integrating the velocity. That’s true, if correctly interpreted. Obviously the velocity of interest (call it v) is not Moe’s velocity relative to Moe’s reference frame, since by definition Moe’s 4-velocity always has components [1, 0, 0, 0] in that frame. Instead, realize that the INS displays position relative to some chosen unaccelerated reference point, and v is Moe’s velocity relative to that point. There is no such thing as absolute position or absolute velocity, but absolute acceleration is well defined and readily measurable. Moe can integrate his acceleration to keep an up-to-date estimate of v, and integrate v to get the position relative to the reference point.

7  Pedagogical Implications

1. We predict that the contracted/dilated approach will eventually die out in favor of the geometric approach. We hope this happens sooner rather than later. The geometric approach seems superior in every way, including simplicity, elegance, power, and consistency.
2. Until that happens, we should avoid asking whether “moving rulers are shorter” or “moving clocks are slower”. Non-experts generally answer yes, while experts answer no. Instead, we should say that proper length and proper time are invariant, so we can speak clearly about ideas, rather than wrangling over mere terminology.
3. The main physics ideas in this article have been well known since reference 7 and reference 2, at the dawn of relativity. Taylor and Wheeler (reference 3) explained the geometric approach with exemplary clarity, at a level that requires only algebra and a little bit of trigonometry. Reference 4 argues that spacetime is as similar to ordinary space as it possibly could be, short of being entirely identical.
4. One big advantage of the geometric approach is backward compatibility, i.e. that it provides an opportunity to review, reinforce, and extend previously-learned ideas. For example, the idea of vector is extended to include 4-vectors, and the idea of rotation in the xy plane is extended to include rotation in the xt plane. Circular trigonometry is extended to include hyperbolic trigonometry.
5. Another big advantage of the geometric approach is forward compatibility, i.e. that it prepares the students for more advanced studies. For instance, when we proceed from special to general relativity, nobody takes seriously Feynman’s parable about rulers that change length from place to place (as discussed in section 8); instead they describe everything in terms of invariant length and proper time. The watchword is, “Time is defined so that motion looks simple.” (reference 8)
6. There is, alas, remarkably little support for the geometric approach in present-day introductory texts. A query addressed to 700 physics teachers via the Phys-L mailing list (reference 9) failed to turn up a single general-physics coursebook that emphasizes the geometric approach. This counts only books intended to serve as the principal text in a high-school physics course or a first-year college physics course, excluding books that would be used in an upper-division course for physics majors, and excluding relativity-only books like Taylor and Wheeler. (reference 3)

   The wide-ranging survey and analysis in reference 10 is valuable, but only tangentially connected to the topic of this article, since it concentrates on invariant (or non-invariant) notions of mass, rather than space and time.

   The continued prevalence of the contracted/dilated approach is disappointing, and there does not appear to be any good reason for it. Simple inertia would be a good-enough argument in favor of tried-and-true techniques, but the contracted/dilated approach is so problematic that it must be considered tried-and-found-wanting, not tried-and-true. The physics-education research (PER) literature (e.g. reference 11) identifies “persistent difficulties” and finds that “Traditional instruction in relativity appears to have little effect on these ideas, which are present among students from the introductory to the graduate level in physics.”

   On the other side of the same coin, there appears to be virtually no published PER comparing the geometric approach to the contracted/dilated approach. Reference 11 mentions Spacetime Physics (reference 3) only in connection with an elective relativity course offered to advanced students. Even then, “Both introductory and advanced courses emphasized length contraction,” leaving us with no information about the merits of emphasizing invariant length.

   In the absence of systematic observations, there are powerful plausibility arguments in favor of the geometric approach, based on well-established pedagogical principles, such as simplicity, elegance, power, and consistency; see also item 10 below.

7. A hard-line manifesto opposing the geometric interpretation can be found in reference 12. I find its arguments to be without merit.
8. The history of science is a poor guide to the teaching of science. Good pedagogy is logical and straightforward, whereas the historical record contains much backtracking out of blind alleys. Especially in an introductory course, students should be given the best explanation for each idea, which is rarely the same as the most ancient explanation. Einstein came to special relativity via a difficult route … but that does not mean present-day students must follow the same route, when an easier and more elegant route – the geometric approach – is readily available. There is no reason why pedagogy must recapitulate phylogeny.

   For what it’s worth: After the geometric approach became available, Einstein adopted it, and relied on it during the development of general relativity. That is a useful hint. Any such appeal to authority must be considered weak evidence, but it is harmless in this case, because it agrees with conclusions we have already reached via other, stronger arguments.

   We are not constrained by the history of who did this-or-that. Instead, we should focus on the reasons for doing this-or-that, and judge the reasons on their merits.

9. There is a profound analogy between time and space, and it is often very helpful to exploit this analogy. However, as the proverb says, no matter what you are doing, you can always do it wrong. We should beware of situations where some timelike concept is associated with a non-corresponding spacelike concept.
   • As an example: time dilation and FitzGerald-Lorentz contraction are commonly mentioned in the same breath, but alas they are not corresponding concepts, for reasons discussed in section 3 and reference 13. This can be misleading to students, making the geometry of spacetime (reference 4) seem less simple than it really is.
   • As a different but equally misleading example: clocks and rulers are often mentioned in the same breath, but are not corresponding concepts (except in the less-than-general case of unaccelerated motion). Some closer correspondences are:

     Space	is to	time
     as odometer	is to	clock
     and as rigid ruler	is to	chordochronometer.

10. The traditional approach to teaching relativity emphasizes that it is weird and rife with paradoxes, using rulers that can’t be trusted and clocks that can’t be trusted. In contrast, we believe that it is pedagogically better to teach students that relativity is not particularly weird or paradoxical; indeed it is in many ways closely analogous to the geometry of ordinary Euclidean space. More than half of what relativity tells is is stuff we already knew, as discussed in section 1.

    In particular, the FitzGerald-Lorentz contraction is the spacetime version of a dejection, in analogy to a diagonal cut across a piece of fabric. Similarly, time dilation is the spacetime version of a simple orthogonal projection, in analogy to the elliptical image of the rings of Saturn.

8  Digression: Spacetime versus Contraction and Dilation

This section is something of a digression, but is included for the sake of completeness. Feel free to skip to section 9 if you wish.

In general, it is common to have two or more ways of accomplishing a given task. At one extreme, humorists including Heath Robinson, Storm P, and Rube Goldberg have invented machines to perform common tasks in ludicrously overcomplicated ways.

In physics, it is the rule rather than the exception to have more than one way of calculating the same thing. It may be that one approach is more accurate in one situation, while another approach is more accurate in another situation. In other cases, it may be merely a difference in convenience. Even when two descriptions make more-or-less equivalent predictions about the observable physics, they may be quite different conceptually and pedagogically.

Historical note: The idea that rulers contract was proposed in reference 14 and reference 15 even before there was a complete theory of special relativity. In 1905, Einstein’s first relativity paper (reference 16) included the idea of clocks that run more slowly when moving. The geometric approach was developed (reference 2) a short time later, in 1908.

Scenario #1: Feynman (reference 17) presented a pair of contrasting qualitative descriptions of general relativity.

a) In one description, the space is flat, but the length of the ruler varies as a function of position.

b) In the other description, the length of the ruler is invariant, but the space is curved.

In this scenario, description (a) is little more than a parable, useful only for a limited range of pedagogical purposes. Within its limitations, its predictions are in qualitative agreement with description (b), but it cannot withstand scrutiny. For quantitative work, we are vastly better off describing general relativity in terms of invariant rulers in a curved space.

Note that these two descriptions should not be used at the same time. If you posit enough ruler-distortion to account for the physics, and additionally posit enough curvature to account for the physics, that would be overdoing it. Perhaps you could describe half the physics one way and half the other way, but this would be pointless and unnecessarily complicated.

Scenario #2: The history of special relativity furnishes another pair of contrasting descriptions:

a) In the early days, it was conventional to say that the mass of an object was greater if it was moving relative to the chosen reference frame. This is called “relativistic mass”.

b) Nowadays it is more conventional to say that mass is invariant, i.e. independent of the choice of reference frame. It is an intrinsic property of the object.

The modern view can be understood by reference to the following very important equation:

where p is the 3-momentum. Note that equation 3 has an elegant interpretation in terms of the dot product of the 4-momentum with itself.

We see that mass and energy are not “the same thing”. Energy is energy (E), and mass is mass (m). Mass tells us the rest energy, as in equation 4. That is, E=m when p=0 – and not otherwise.

Tangential remark: You may have been told 100 times that energy can be «converted» or «transformed» into energy in accordance with the famous E=mc² formula. That’s less than half true. In reality, in some sense rest energy can be converted to other, more-noticeable forms of energy, but equation 4 is less than half the story. The details are outside the scope of this article.

One problem with the idea of “relativistic mass” is that there are at least three inequivalent ways of defining it. One approach is to define it as E/c² where E is the total energy, in contrast the invariant mass E_rest/c² in accordance with equation 4. Using this approach, the “relativistic mass” is greater than the plain old mass by a factor of γ, where:

Another attempt to define “relativistic mass” starts from the claim that mass “must” increase, because mass measures “resistance to acceleration”, and a fast-moving particle is observably more resistant to acceleration than its “rest mass” alone would predict. For straight-line acceleration, we find that this “relativistic mass” is greater than the plain old mass by a factor of γ cubed. This is confusing, to say the least, because it conflicts with the previous paragraph, which involved only γ to the first power.

It is much simpler to just forget the idea of relativistic mass. As discussed in reference 18, it is perfectly possible to understand the relativistic decrease in the 3-acceleration without mentioning mass at all. The 3-acceleration can be seen to be smaller than the spacelike part of the proper acceleration for reasons having nothing to do with mass, merely to do with projections and the geometry of spacetime.

A third approach to “relativistic mass” uses circular motion, unlike the the straight-line motion considered above. As discussed in reference 18, this gives yet another numerical value for the “relativistic mass”, conflicting with both of the previous attempts. It’s not very convenient to have a “relativistic mass” that depends on direction. Mass should be a scalar.

Given this threefold inconsistency and other problems, it makes sense to forget about “relativistic mass”. The modern, sensible approach is to describe the physics in terms of the invariant mass, proper length, and proper time. Then at the end of the day, the solution can be projected onto the laboratory frame if necessary.

In passing we remark that the shift in emphasis from (a) to (b) was accompanied by a shift in terminology. Nowadays experts (and many non-experts as well) conventionally speak of “the” mass of the proton as being about 1 dalton. It would be redundant to call this the “rest” mass or the “invariant” mass; we just call it the mass. In contrast, some (reference 19) (but not all) early references spoke of non-constant masses. In any case, we do not wish to argue about terminology; the contrasting ideas are more important than the conflicting terminology.

Scenario #3: We now turn away from analogies and discuss something directly relevant to the topic of this article, namely a pair of contrasting descriptions of length and time:

a) One description alleges that rulers are shorter when they are moving relative to some chosen reference frame; this is known as the FitzGerald-Lorentz contraction (reference 14 and reference 15). It also alleges that clocks run more slowly when they are moving relative to some chosen reference frame; this is called time dilation or time dilatation. (reference 20)

b) The other description focuses attention on the proper length of rulers and the proper time of ordinary clocks.

Either of these descriptions – if you get the details right – can be used to predict and/or describe the correct physics. However, you must be careful not to use both of them at the same time. You cannot compute the FitzGerald-Lorentz contracted length and then project it onto another frame. Either the ruler gets shorter or it doesn’t; you can’t have it both ways.

When choosing which description to use, one should consider such factors as simplicity, elegance, power, and compatibility with other descriptions and models.

9  Summary

The way relativity has heretofore been taught to the general population – and to the next generation of physics teachers – makes things seem far more complicated than they really are. It is out of step with the way experts think about the subject, and has been for many decades. It is not technically wrong, just pedagogically inferior to the geometric approach.

We call attention to a pair of simple yet powerful ideas: treating time and space on the same footing, and treating boosts and rotations on the same footing. This gives us a nice way of visualizing special relativity:

As everybody knows, the length of a ruler is invariant under rotations.

That tells us the length of a ruler is invariant under boosts.

In turn, that tells us the time between ticks of an ordinary clock is invariant under boosts (and rotations).

The defining property of an ordinary clock is that it ticks at a steady rate, marking off uniform intervals of proper time. An ordinary clock carried on a journey behaves more like an odometer than a rigid ruler, recording proper time, not chord time. If you want to know the chord time, you need to carry something more complicated than an ordinary clock, i.e. something like an INS.

10  Acknowledgments and References

Thanks to Antti Savinainen, Joel Rauber, and the other members of the phys-l mailing list for many valuable contributions.

1.

John Denker,
“Welcome to Spacetime”
www.av8n.com/physics/spacetime-welcome.htm

2.

H. Minkowski,
“Raum und Zeit”,
80. Versammlung Deutscher Naturforscher (Köln, 1908). Published in Physikalische Zeitschrift 10 104-111 (1909) and Jahresbericht der Deutschen Mathematiker-Vereinigung 18 75-88 (1909).
http://de.wikisource.org/wiki/Raum_und_Zeit_(Minkowski)

3.

E.F. Taylor and J.A. Wheeler,
Spacetime Physics
W.H. Freeman, San Francisco, CA, (1963).

4.

John Denker,
“The Geometry and Trigonometry of Spacetime”.
www.av8n.com/physics/spacetime-trig.htm

5.

John Denker,
“Introduction to Vectors”
www.av8n.com/physics/vector-intro.htm

6.

E. Minguzzi,
“Differential aging from acceleration: An explicit formula”
Am. J. Phys. 73 876 (September 2005).

7.

H. Poincaré,
“Sur la dynamique de l’electron”,
Rendiconti del Circolo matematico di Palermo, 21, 129–176 (1906); see also Comptes Rendues 140, 1504–8 (1905).
http://www.soso.ch/wissen/hist/SRT/P-1905.pdf

8.

C.W. Misner, K.S. Thorne, and J.A. Wheeler,
Gravitation
(W.H. Freeman, San Francisco, CA, 1973).

9.

Forum for Physics Educators
http://www.phys-l.org/mailman/listinfo/phys-l

10.

Gary Oas,
“On the abuse and use of relativistic mass”
http://arxiv.org/abs/physics/0504110

11.

R.E. Scherr,
“An investigation of student understanding of basic concepts in special relativity” (Dissertation, University of Washington, 2001)
http://www.physics.umd.edu/perg/papers/scherr/dissertation/ScherrDisstn.pdf

12.

D. Bohm and B.J. Hiley,
“Active interpretation of the Lorentz ‘boosts’ as a physical explanation of different time rates”
Am. J. Phys. 53 8 (August 1985).

This article asserts “an accelerated system actually has a changed time rate” but offers no evidence of this, just prejudice and “proof” by bold assertion. It dismisses evidence to the contrary, giving no reason other than the fact that the evidence disagrees with prejudices. It fails to consider – or even mention – other explanations (such as the geometric approach) that agree with the evidence. It fails to cite the relevant prior literature.

13.

J.H. Field,
“Two novel special relativistic effects: Space dilatation and time contraction”
Am. J. Phys. 68 (4) (April 2000).

14.

G.F. FitzGerald,
“The Ether and the Earth’s Atmosphere”
Science 13, 390 (1889).

15.

H.A. Lorentz,
“De relatieve beweging van de aarde en den aether”,
Koninklijke Akademie van Wetenschappen te Amsterdam 1 74–79 (1892).

16.

A. Einstein,
“Zur Elektrodynamik bewegter Körper”
Annalen der Physik 17, 891 (1905).
./refs/einstein-1905-elektrodynamik.pdf

17.

Feynman, Leighton and Sands,
The Feynman Lectures on Physics Volume II chapter 42 (Addison-Wesley, Reading, MA, 1964)

18.

John Denker,
“Acceleration in Spacetime”.
www.av8n.com/physics/spacetime-acceleration.htm

19.

A. Einstein,
“Über eine Methode zur Bestimmung des Verhältnisses der transversalen und longitudinalen Masse des Elektrons”
Annalen der Physik 21, 583 (1906).
./refs/einstein-1906-transversalen-und-longitudinalen-masse.pdf

20.

J. Larmor,
“On a Dynamical Theory of the Electric and Luminiferous Medium”,
Phil. Trans. Roy. Soc. 190, 205-300 (1897).