Figure 1: Hyperbolic Rocket Trajectories
This assumes you already know the basic ideas of special relativity from a modern viewpoint. If in doubt, please review reference 1 before proceeding.
Suppose Moe undergoes an acceleration a. The acceleration may be varying as a function of time, but for simplicity we assume the spacelike components of the velocities and accelerations are all in the ±x1 direction, so only one spatial dimension is involved.1 Here a is the proper acceleration, i.e. the acceleration as perceived by Moe. Similarly τ (“tau”) denotes proper time, i.e. the elapsed time as perceived by Moe. We do not assume Moe’s velocity (relative to the lab frame) is small compared to the speed of light, so we will need to analyze things using special relativity.
We start by considering a short period of time Δτ. If Δτ is short enough, we can make two crucial simplifications:
Because a(τ) Δτ is small compared to the speed of light, we can make use of an instantaneously comoving unaccelerated frame. That is, we find a frame that is – unlike Moe’s frame – unaccelerated, but which happens to have a velocity that is the same as Moe’s velocity at time τ. In this frame, we can understand what’s going on in purely classical terms, using nothing more than high-school physics, because all the velocities of interest are small, and in accordance with the correspondence principle, special relativity must be the same as classical physics under these conditions.
The next step in the analysis is to make use of the geometry of spacetime. It is well known even in pop culture that time is the fourth dimension; we just need to understand what that means in precise technical terms. The fourth dimension is obviously not the exactly same as the other three, but it is more nearly the same than most people realize.
Let us consider the various types of rotations in this four-dimensional space (Minkowski space). This is discussed in detail in reference 2, but the main points can be summarized here:
| Terminology: A rotation in the x,y plane is just an ordinary spacelike rotation. | A rotation in the x,t plane is called a boost. |
| Additivity: If we rotate something by an angle θ1 and then rotate it some more in the same direction by an angle θ2, the overall rotation is described by θ = θ1 + θ2. | If we boost something by a rapidity ρ1 and then boost it some more in the same direction by a rapidity ρ2, the overall boost is described by ρ = ρ1 + ρ2. |
| Nonlinearity: The slope m is a nonlinear function of angle, namely m = tan(θ) | The velocity v is a nonlinear function of rapidity, namely v = tanh(ρ). |
| First-order: For small angles, we have simply m = θ, assuming θ is measured in radians. | For small rapidities, we have simply v = ρ, assuming we are using units such that the speed of light is equal to unity. |
Because of the first-order property mentioned above, in the instantaneously comoving frame we can write
| Δρ = a1(τ) Δτ (1) |
If we temporarily assume the acceleration is steady, i.e. not a function of time, then we can use the additivity property to write simply
| ρ(τ) = a1 τ + const (2) |
More generally, whether or not the acceleration is steady, we can write:
| ρ(τ) = | ∫ |
| a1(τ′) dτ′ (3) |
where once again we are making heavy use of the additivity property. We write the acceleration with a subscript to indicate we are talking about acceleration in a particular direction, in this case the “1” direction.
Now let us turn our attention to the topic of velocity.
Suppose Moe has four-dimensional position x. We can project this four-vector onto the reference frame of some observer Joe. We use the following notation for representing a vector in terms of its components:
| x = | ⎡ ⎢ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎥ ⎦ |
| (4) |
In the case of position vectors we use t as a synonym for x0 to denote the timelike component of x in a specified frame.
Quite independently of any observer, we can define Moe’s four-dimensional velocity as simply
| u := |
| (5) |
If we take this 4-velocity and project it onto the axes of Moe’s reference frame, we get the result shown in equation 6. This is simple and unsurprising, but nevertheless quite useful:
| u = | ⎡ ⎢ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎥ ⎦ |
| (6) |
Moe is at rest with respect to his own reference frame, which means that the spacelike components of his velocity is zero, but his 4-velocity is not zero. The timelike component of his 4-velocity tells us that he is moving forward along his world-line at the rate of 60 minutes per hour.
Next, if we take this same 4-velocity vector and project it onto Joe’s reference frame, we get:
| u = | ⎡ ⎢ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎥ ⎦ |
| (7) |
There is nothing surprising about this result; we have just treated Moe’s velocity vector like any other vector, and projected its components onto Joe’s axes, using the same projection matrix that we would use for any other 4-vector:
| ⎡ ⎢ ⎣ |
| ⎤ ⎥ ⎦ |
| = | ⎡ ⎢ ⎣ |
| ⎤ ⎥ ⎦ | ⎡ ⎢ ⎣ |
| ⎤ ⎥ ⎦ |
| (8) |
which is well-nigh unforgettable, by analogy to the familiar spacelike rotation matrix. The main difference is that here we use hyperbolic trig functions (sinh and cosh), instead of the more familiar circular trig functions (sin and cos). See reference 2.
We emphasize that this is the vector u remains the same physical vector, even though different observers represent it using different sets of components. For more about the distinction between physical vectors and components, see reference 3.
We now come to a tricky point. Consider the following contrast:
| In any frame, the 3-vector position is given by the three spacelike components of the 4-vector position. Similarly, the 3-momentum is given by the three spacelike components of the 4-momentum | Beware: by long-standing convention, the reduced velocity v is not given by the three spacelike components of the 4-velocity u. |
Specifically, in any frame the reduced velocity is defined as:
| (9) |
where S stands for “spacelike part”. It must be emphasized that v is a derivative with respect to frame-time t, in contrast to the proper-time τ which appeared in equation 5.
This is a notorious trap for the unwary. For more on the contrast between reduced velocity and 4-velocity, see reference 4.
By the chain rule, we can write
| (10) |
so we see that the reduced velocity is smaller than the spacelike part of the 4-velocity by a factor of γ (“gamma”). From equation 5 and equation 4 we see that γ is simply:
| (11) |
In particular, we see that under prolonged acceleration, the spacelike part of the 4-velocity increases without bound; indeed sinh(ρ) eventually increases exponentially as a function of ρ. In contrast, the reduced velocity does not increase without bound; tanh(ρ) increases toward an asymptotic value of 1.
The proper acceleration is of course
| a := |
| (12) |
We can find the components of a in Joe’s frame by differentiating equation 7.
| (13) |
We cannot easily find the components of a in Moe’s frame by differentiating equation 6, because the definition of what we mean by “Moe’s frame” is changing as a function of time. However, we can easily do the calculation in the instantaneously comoving unaccelerated frame. In fact, all we need to do is evaluate the previous expression for the case of ρ=0. That tells us the acceleration can be expanded in terms of components in Moe’s frame as:
| (14) |
This doesn’t tell us anything new, but it is a check on our work, confirming that the thing we have been calling a1 was named correctly, since it is the relevant component of the proper acceleration in Moe’s frame.
The final step in this line of reasoning is to calculate the 3-acceleration, A:
| (15) |
where we have made use of several hyperbolic trigonometric identities; see reference 5 or reference 6 if you need a reminder. It is also easy to rederive them from scratch, starting from the definition of sinh and cosh in terms of exponentials.
Equation 15 expresses a well-known result; compare e.g. equation (7.14) in reference 7. In this expression, a1 can depend on t, and of course γ is implicitly dependent on t.
Let us now consider the case of circular motion, where the acceleration is directed perpendicular to the velocity, and is uniform in magnitude.
Rather than derive the solution, let’s just write it down. The solution for non-relativistic circular motion is well known, and we can easily patch it up to handle the relativistic case. The 4-velocity must have the form:
| (16) |
where the angle θ is a steadily-increasing function of time, and ρ and r are independent of time. You can verify that this satisfies the normalization condition u·u = −1.
The 4-vector position must have the form:
| (17) |
You can verify that this describes circular motion, in the sense that if we project x onto three dimensions, we get a circle of radius r.
Differentiating the position with respect to proper time we get:
| (18) |
Comparing that to equation 16, we find
| (19) |
which makes sense. This determines ρ as a function of the radius and rate of motion. The value of ρ is independent of time.
The 4-vector acceleration is
| (20) |
You can easily verify that the 4-acceleration is perpendicular to the 4-velocity.
The conventional 3-vector velocity is
| (21) |
The conventional 3-vector acceleration is
| (22) |
You can easily verify that the spatial part of the acceleration is perpendicular to the spatial part of the velocity.
Note that for relativistic circular motion, the 3-acceleration (A) is smaller than the spatial part of the 4-acceleration (a123) by two factors of gamma, i.e. two factors of dt/dτ.
In section 1.1 we saw that the 3-acceleration is smaller than the spacelike part of the 4-acceleration by a factor of γ cubed. This has nothing to do with “relativistic mass” or anything like that; we have not even mentioned mass until now. Everything that is going on can be adequately explained by the definition of 3-acceleration, and by the geometry and trigonometry of spacetime.
For more about the structure of spacetime, see reference 2.
Some people are tempted to say that a fast-moving object is more “resistant to acceleration”. However, our analysis shows that it is more consistent to say that the object accelerates just fine, especially as measured in its own frame, but the projection of that acceleration onto the lab frame is foreshortened.
Also, some people take the factor of gamma cubed and fold it into their definition of mass, so that mass will be “the” measure of “resistance to acceleration”. That’s obviously not going to work, because in section 1.2 we found a factor of gamma squared, not gamma cubed. Meanwhile they sometimes write Etotal = mc2 instead of Erest = mc2, which gives them yet another notion of “the” relativistic mass, with involves only one factor of gamma.
So we see that people have at least three different notions of “the” relativistic mass. Sometimes they try to wriggle out of this mess by defining a “transverse mass” different from the “longitudinal mass”. Let’s not go there.
The modern (post-1908) view is to say that the mass is invariant. The mass is a Lorentz scalar. The factors of gamma that crop up in the equation of motion are not part of the mass; they just account for the projection of the 4-acceleration onto the lab frame, and account for the conventional definition of 3-acceleration (which involves d/dt instead of d/dτ). For more on why it is advantageous to use invariant mass and proper time, see reference 8 and reference 9.
For a particle of mass m, we define the 4-momentum p to be:
| p := m u (23) |
which is exceedingly important because of its connection to the laws of motion, including conservation of energy and conservation of momentum.
We can check that in the correspondence limit, when all velocities are small compared to the speed of light, equation 23 reduces to the well-known classical result
| p123 := m v for v ≪ c (24) |
where as before the subscript S indicates the spacelike part.
| In accordance with modern practice the quantity we are calling “the” mass is a Lorentz scalar. It is independent of velocity. It is the same in all reference frames. It would be harmless but redundant to call it the invariant mass or the rest mass; normally it is just called “mass”. | We avoid and deprecate all notions of velocity-dependent mass or “relativistic mass”. Such notions are archaic and are inconsistent with the four-dimensional spacetime point of view. See reference 9. |
In analogy to equation 4 we can expand p in terms of components:
| p = | ⎡ ⎢ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎥ ⎦ |
| (25) |
where we use the term E as a synonym for p0 to denote the energy, i.e. the timelike component of the 4-momentum in a specified frame.
If we take the dot product of p with itself, we obtain:
| (26) |
We find that the famous equation E=mc2 does not refer to the total energy, but only to the rest energy, i.e. the energy that the particle has when its reduced velocity is zero.
We also see that if p as defined by equation 23 is to be a well-behaved four-vector, then m must be a Lorentz scalar (and vice versa).
Reference 10 contains an example illustrating the power of equation 26, showing how it can be applied to achieve a remarkably easy solution to a nontrivial problem, i.e. calculating the energy required for a machine to make antimatter.
Suppose Joe sets up an electric field that is uniform in the lab frame, uniform over all times and places of interest. Let the electric field vector point in the x1 direction. Let Moe be comoving with a free particle of mass m and charge q that is initially at rest and thereafter accelerates under the influence of the field.
Exercise: Find the proper acceleration as a function of time.Note: As usual, there are multiple ways of solving the problem … some of them more elegant than others.
Huge hint: There is a way to solve this problem in your head.
As discussed in reference 11, the geometric-algebra version of the Lorentz force law is:
| p = q u · F (27) |
where F is the electromagnetic field bivector. The first step in the easy way of doing this exercise is to think about the symmetry. We know that in general, a field F that is purely electric in one frame will have electric and magnetic components in other frames. That’s true in general, but it’s not what happens in this case. Ask yourself, in what direction would the magnetic field be pointing? The only directions in the statement of the problem are the time direction and the x1 direction. The electric field bivector lies in the plane spanned by those two directions. Any magnetic field bivector requires two spacelike directions. There’s no way that can happen if the motion is aligned with the field. Therefore we conclude that B=0 in Moe’s frame, no matter how fast Moe is moving in the x1 direction.
The second step is to remember that the gorm of any vector or bivector is an invariant scalar, the same in any reference frame. In any frame where we know F in terms of the E and B vectors, the gorm of F is B2 − E2. Since B=0 in all frames of interest, E must be the same for both Joe and Moe.
We conclude that the proper acceleration is given by a1 = E1 q / m. That’s about as simple as it could possibly be.
A less-elegant approach would be to write F = E1 γ0∧γ1 in Joe’s frame, transform both basis vectors into Moe’s frame according to equation 8, and collect terms to show that the field is the same in all frames of interest.
To find Moe’s position 4-vector x, it suffices to integrate his velocity u. One way to do this is to find the projection of x onto Joe’s reference frame, by integrating equation 7 component-by-component. The integrals may be easy or hard, depending on how the acceleration varies as a function of time.
For the rest of this section, we restrict our attention to the simple case of steady proper acceleration, i.e. a(τ) independent of τ, such as we saw in section 2.3. Therefore in accordance with equation 2 we have ρ(τ) = a1τ′, where τ′ differs from τ by some constant of integration. Integrating equation 7 gives us:
| x′ = |
| ⎡ ⎢ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎥ ⎦ |
| (28) |
where x′ differs from x by yet another constant of integration.
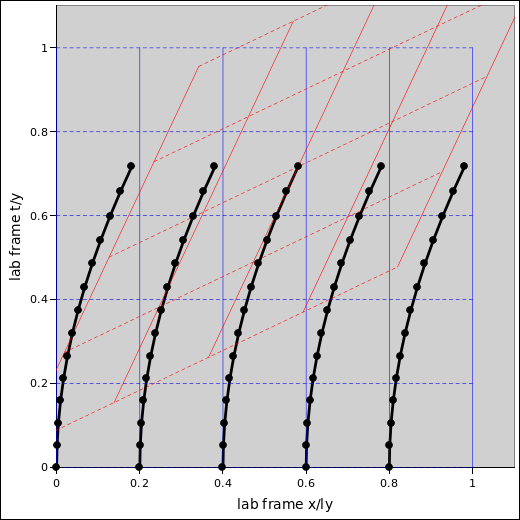
On a spacetime diagram, the graph of equation 28 is a hyperbola. For this reason, uniformly accelerated motion is called hyperbolic motion. Five examples of this are shown in figure 1.
If it’s not obvious that equation 28 describes a hyperbola, contemplate the identity cosh2 − sinh2 = 1.
The hyperbolic motion of an extended object is discussed in more detail in reference 12. This includes an explanation of figure 1. See also reference 13.