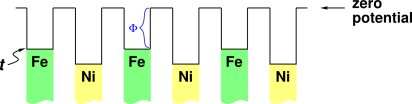
Figure 1: Electrochemical potential; electrical neutrality, not equilibrium
The purpose of this section is to introduce the idea of an equilibrium electric field and to quantify it in terms of the work function. This has all sorts of practical applications, including electrochemical cells (aka batteries), as as discussed in reference 1.
We will give a plausibility argument in the form of a Gedankenexperiment.
Start with a chunk of nickel. Make sure it is electrically neutral .
Also take a corresponding chunk of iron. It has the same FCC crystal structure as the nickel, although the lattice spacing will be slightly different. It also starts out electrically neutral.
As we shall see, these two electrically-neutral pieces of metal attract electrons differently. We give a name to this: we say they have different work functions. The work function measures the energy required to take an electron from the surface of the metal to some far-away place.1
Work functions can be understood in terms of basic principles including electrostatics and the Pauli exclusion principle, as discussed below. Calculating things like work functions ab initio would be quite a tour de force, and we need not discuss the details here. We will accept the observed work function values and then make some plausibility arguments.
| Element | Work function | |
| Cs | cesium | 2.1 eV |
| Ag | silver | 4.26 eV |
| Al | aluminum | 4.28 eV |
| Zn | zinc | 4.33 eV |
| Fe | iron | 4.5 eV |
| W | tungsten | 4.5 eV |
| Cu | copper | 4.65 eV |
| Ni | nickel | 5.15 eV |
| Au | gold | 5.1 eV |
| Pt | platinum | 6.35 eV |
The fact that a metal has some sort of nonzero work function is not particularly hard to understand. The electrons want to be near the metal nuclei, in accordance with the basic principles of electrostatics, such as Coulomb’s law. Even if the metal chunk is slightly negatively charged it will attract electrons. Indeed even a single neutral atom will attract electrons – the H− ion in vacuum has lower energy than a hydrogen atom and electron separately. A larger object with the same work function will attract an electron more easily, because its capacitance is lower. (The work function is defined with respect to a geometrical situation where the capacitance is large enough so that capacitive effects are negligible.)
The fact that different materials have different work functions is perfectly understandable also. Different materials have a different spacing between nuclei. So think of it as a simple quantum-mechanical particle-in-a-box problem: The smaller the box, the higher the kinetic energy the electrons must have. You can even make a connection between the work function (a purely electrical property) and the elastic properties of the metal: when you squeeze the chunk of metal you squeeze the electron wavefunctions, and that raises their kinetic energy.
Let’s look at this idea in more detail. The following is accurately true for one metal compared to a compressed piece of the same metal, and true to a first approximation for nickel compared to iron. Suppose we have two pieces of metal with the same number of conduction electrons, the same crystal structure, and similar overall shape. Then there must be a one-to-one correspondence between their conduction-band wavefunctions. The wavefunctions in the smaller box will (to a first approximation) look the same as those in the larger box, just scaled to a smaller wavelength so they fit in the box. Smaller wavelength λ means higher momentum p = h/λ, hence higher kinetic energy Ek = p2/2m.
To obtain a better approximation, you would need to take into account other contributions to the energy. For starters, there is a contribution to the potential energy from the fact that a nickel atom has more protons than an iron atom. That difference is mostly compensated by an equal difference in the number of non-conduction electrons, but then those extra electrons affect the kinetic energy of the conduction electrons (via the exclusion principle).
Remember, the point of this section was just to make it plausible that different materials have different work functions. For our purposes, we do not need to calculate accurate work function values from first principles. It suffices to accept the experimentally observed values.
To more fully understand the origin and meaning of the work function, we must make a careful distinction: a test charge is not the same as a real electron.
First, arrange for both chunks of metal to be identical in size and shape. File one of them down if necessary. This won’t change the work function. The objective is to make both chunks have the same self-capacitance. At this point, they are both still electrically neutral. A test charge placed on the iron chunk creates the same electrical field pattern and has the same energy as a test charge placed on the nickel chunk. So the test charge is equally happy either place.
But test charges do not exist in nature. Equilibrium is not established by the exchange of test charges, or alpha particles, or muons. In practical situations (with a few important exceptions, as we shall see), equilibrium is established by exchange of electrons. Real electrons.
The Pauli exclusion principle involves electrons excluding other electrons. It means that electrons are happier being on the nickel chunk than the iron chunk – even though a test charge would be equally happy.
Figure 1 shows the electron’s "unhappiness function" (i.e. electrochemical potential) when the metal chunks are electrically neutral. This is not the equilibrium situation.
The black line in the diagram represents the energy level of the electron, as a function of position. The green and yellow shaded regions are meant to represent the Fermi sea within the chunks of metal. The bottom of the Fermi sea is not interesting, because it is impossible to inject an electron into this level (by the exclusion principle), and it is energetically unfavorable to extract an electron from this level. Figure 1 does not attempt to accurately portray the bottom of the Fermi sea.
What matters is the top of the Fermi sea. The top of the Fermi sea for iron is labeled t in the diagram. The most easily-added electron will go in just above this level, and the most easily-extracted electron will come out from just below this level. (This corresponds to the LUMO and HOMO in molecular physics – but if that doesn’t mean anything to you, don’t worry about it.)
The length of the vertical steps in the black line represent the work function of the associated chunk of metal, i.e. the energy that the electron loses if it gets ejected from the metal, via the photoelectric effect or whatever. The work function for iron is labeled Φ in the figure.
In the figure I have indicated a “zero level” for the potential This choice is arbitrary and has does not affect the physics in any way. In this case I have chosen the energy of an isolated far-away electron in the vacuum to be the reference point for zero potential.
Next, figure 2 shows the electrochemical potential when equilibrium has been established by exchange of electrons:
In equilibrium, the nickel chunks have a definite excess of electrons, and the iron chunks have a definite deficit. In the gaps, there will be an electric field, as indicated by the blue arrows. In the gaps – but not within the metals – the energy per electron can be equated to the conventional electric potential (with the usual minus sign). Within the metals, we won’t even talk about the electric potential, because it is irrelevant. What matters is the electrochemical potential, which contains a huge contribution from the kinetic energy of the electrons.
The magnitude of the electric field in the gaps is equal to the work-function difference divided by the length of the gap, if we assume a nice parallel-plate geometry. Now the surface charge on each plate is proportional to the electric field, so we discover that the amount of charge depends inversely on the gap. (You can wiggle the gap and measure how much current needs to flow in order to maintain equilibrium. This is a way to measure work functions. You can even add a potentiometer and make it a null measurement. This is called a Kelvin bridge or Kelvin probe. For the next level of detail on this, see reference 2.)
Imagine the metal chunks are arranged in a big circle, so we have periodic boundary conditions on the diagram.
Now suppose we hook up certain pairs using aluminum wire in the usual way, the way batteries are hooked up, as shown in figure 3.
The details of the aluminum are not very interesting; its main function is to ensure that the attached Fe and Ni remain in electron-equilibrium. Aluminum conducts electrons quite well; it does not conduct muons or alpha particles or “test charges”.
So far there is nothing special about this setup. An electron is equally happy in any of the various chunks of metal. There is an electric field in the gaps. There is a huge "dipole layer" at the Fe/Al interface and also at the Al/Ni interface. You can think of a dipole layer as a near-infinite electric field over a near-zero distance. Let x be the effective thickness of the metal/metal interface. As x becomes small, the electrical field grows like 1/x, so the potential difference remains independent of x and remains equal to the work-function difference. The Fe and Ni pieces are at the same potential here as they were back in figure 2.