Figure 1: Multiplication by 1
Copyright © 2007 jsd
Short multiplication refers to any multiplication problem that consists of multiplying a one-digit number by another one-digit number. That means everything from 0×0 through 9×9.
Long multiplication refers to multiplying multi-digit numbers. We are about to discuss a highly efficient algorithm for doing this.
As a prerequisite for doing long multiplication, you need to be able to do short multiplication reliably.
Your short multiplication will get faster, gradually over time. The short multiplication facts will solidify in your memory, gradually over time. Indeed, long multiplication gives you plenty of practice doing short multiplication, so we can kill two birds with one stone.
For a video discussing this topic, see reference 1. For some basic, general-purpose hints on how to do math, see reference 2. For a discussion of long division, see reference 3.
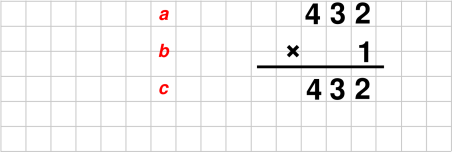
Let’s start by doing a super-simple example. Let’s multiply 432 by 1. You can do that in your head. The answer is written out in figure 1, in the standard form used for long multiplication problems.
Multiplication by 2 is almost as easy, as shown in figure 2:
Multiplication by 20 is also easy; all we need to do is shift the previous result over one place, as shown in figure 3:
Here’s a more interesting example. Let’s multiply 432 by 21. We can reduce the workload if we rewrite 21 as 20+1. We can express that as an equation:
| (1) |
So now we are multiplying 4321×(20+1). The equation is:
| (2) |
There are two ways of understanding where equation 2 comes from. One way is to start with equation 1 and multiply both sides by 432. Another way is to start with the left-hand side of equation 2 and replace the 21 by something that is equal to it; in other words, to do a substitution.
We can apply the distributive law to the right-hand side of equation 2. That gives us:
|
Both of the multiplications in equation 3b are easy, and indeed we have already done them. Plugging in the results of these multiplications gives us:
|
So at this point, there’s no more multiplying to be done. All that remains is a simple addition problem, as shown in figure 4. The multiplication problem shown in gray is exactly equivalent to the addition problem shown in black.
Note that we can get by without writing the zero at the end of line d in the figure. The bottom-line result is the same, whether we write this zero or not, provided we keep things properly lined up in columns, as shown in figure 5. In the number system we are using, the Hindu number system, we normally think of zeros like this as being necessary to indicate place value. However, that’s not strictly true. You don’t need to write the zeros, provided you have some other way of keeping track of place value.
You are allowed to write the zero (as in figure 4) if that’s convenient, but you are also allowed to skip it (as in figure 5) if that’s more convenient.
Long multiplication depends on lining stuff up in columns, as a way of keeping track of place value. Therefore, when learning to do long multiplication, use graph paper. This will help you keep things properly lined up. Tidyness counts for a lot when doing long multiplication.
After you’ve done hundreds of these things, and have learned to be super-tidy, you can do without the graph paper, but until then you’ll save yourself a lot of grief if you use graph paper. The best thing is to get a lab book, which is a bound book containing blank graph paper on every page. Such things are cheap and readily available from office-supply stores. The second-best thing is to use graph paper in pad form, or perhaps loose-leaf form. If you have a printer attached to your computer, there are apps that will print graph paper for you, in any imaginable style.
Note that numbers tend to be taller than they are wide. For this reason, rather than writing every row of numbers on the lines of the graph paper, it looks nicer if each row of numbers is 1½ lines below the previous one. You can see how this works in the figures in this section.
The principle here is that the graph paper is supposed to help you, not hobble you. If using the vertical lines is helpful, use the vertical lines. If using the horizontal lines in the obvious way is not optimal, use them in some less-obvious way.There are always lots of people trying to make you color inside the lines, but any kind of originality, artistry, or creativity requires coloring outside the lines. Math, if it’s done right, involves lots of creativity. Don’t be afraid to color outside the lines.
Let’s do one more example. Let’s multiply 432 by 211. We use the same trick as before: We pick 211 apart, digit by digit. That is, we write 211 = 200 + 10 + 1. Multiplying by 200 is easy; just multiply by 2, and then shift the result two decimal places. The whole procedure can be carried out very efficiently, if you organize it properly, as shown in figure 6.
The recipe for doing long multiplication is based on simple ideas:
We will mostly use the same approach as we used in section 2. The only difference is that this time we will need to pick apart both of the factors into their individual digits. (Previously we only picked part the second factor.)
As mentioned in section 2, the rationale for doing things this way is based on the distributive law and the axioms of the number system. This is discussed in more detail in section 3.5.
There is an easy and reliable method for arranging the calculations. We illustrate the method using the question shown in figure 7.
The first step is to write down the question. It is important to line up the numbers as shown, so that the ones’ place of the top number lines up with the ones’ place of the bottom number, and so on for all the other digits. Keeping things aligned in columns is crucial, since the colums represent place value. As mentioned in reference 2, tidiness pays off.
If one of the factors is longer than the other, it will usually be more convenient to place the longer one on top. That’s not mandatory, but it makes the calculation slightly more compact.
You may omit the multiplication sign (×) if it is obvious from context that this is a multiplication problem (as opposed to an addition problem).
We proceed digit by digit, starting with the rightmost digit in the bottom factor, and proceeding systematically right-to-left. We do things in order of increasing place value, right to left. That makes sense, especially when doing additions, because a carry can affect the next column (to the left), but never the previous column. This is opposite to the direction of reading English text, which is unfortunate, but there’ s nothing we can do about it.
So, let’s look at the rightmost digit in the bottom factor in our example. It’s a 1. We multiply this digit into each digit of the other factor, digit by digit, working systematically right-to-left across the top factor.
We place these results in order in row c, with due regard for place value. The 1×7 result goes in the ones’ place, the 1×6 result goes in the tens’ place, and the 1×5 result goes in the hundreds’ place, and so forth, as shown in row c in figure 8. Actually, multiplication by 1 is so easy that you can just copy the whole number 4567 into row c without thinking about it very hard. So far, this is just like what we did in section 2.
Note: You may wish to leave a little bit of space above the numbers in row c, for reasons that will become apparent later.Also note: In all the figures in this section, anything shown in black is something you actually write down, whereas anything shown in color is just commentary, put there to help us get through the explanation the first time.
That is all we need to do with the low-order digit of the bottom factor. We now move on to the next digit of the bottom factor. In this case it is a 2.
At this point in this example, things get interesting, because some of the short-multiplication results are two digits long. There is no way to write all of them in a single row. Fortunately, we are allowed to use multiple rows. One possibility is to spread things out as shown in figure 9. We write 2×7=14 in row d, and then write 2×6=12 on row e, and so on.
It is theoretically possible to write the product 4567×2 on a single row, but this would require doing a bunch of additions, but we choose not to do that. We are going to do all the short multiplications first, and then do all the additions later. This requires slightly more paper, but it is vastly easier to do, easier to understand, and easier to check.
As previously mentioned, the procedure is to pick a digit from the lower factor, and multiply this digit into each digit of the upper factor. The result of the first such multiplication is 2×7=14, which we place in row d. Alignment is crucial here. The 14 must be aligned under the 2 as shown. That’s because it “inherits” the place value of the 2.
Next we multiply 2×6=12. You might be tempted to write this in row d, but there is no room for it there, so it must go on row e, as shown in the figure. Again alignment is critical. This product is shifted one place to the left of the previous product, because it inherits additional place value. It inherits some from the 2 (in the bottom factor) and some from the 6 (in the top factor). Since we are working systematically right-to-left, you don’t need to think about this too hard; just remember that each of these short-division products must be shifted one place to the left of the previous one, as suggested by the diagonal dotted blue line in figure 9.
Let me explain the color-coded backgrounds. In row d, the 14 has a yellow background, because it is derived from the 7 in row a, which has a yellow background. Similarly the 12 in row e yas a pink background, because it is derived from the 6 in row a, which has a pink background.
Although figure 9 is good for illustrating the principles involved, it is unnecessarily spread out. It would be better to write things more compactly, as shown in figure 10, because this makes it easier to keep things properly aligned. (The objective here is not to save paper. Remember, paper is cheap, and trying to save paper is almost always a bad idea. The advantage of the compact representation is that it makes it easier to keep things lined up in columns.)
Note the pattern of placing successive short-division results on alternating rows. There is guaranteed to be enough room to do this, because the product of two one-digit numbers can never have more than two digits.
We are now more than half-way finished.
At this point (or perhaps earlier), if you are not using grid-ruled paper, you should lightly sketch in some vertical guide lines. The tableau has become large enough that there is some risk of messing up the alignment, i.e. putting things into the wrong columns, if you don’t put in guide lines.
That’s all for the “2” digit in the bottom factor. We now proceed to the “3” digit. We multiply this by each of the digits in the top factor, in the now-familiar fashion. All the short-multiplication results from this step are put in rows f and g.
At this point, all of the short multiplications are complete. In figure 11, you can see where everything comes from. The color-coded background indicates which digit of the upper factor was involved, and the row indicates which digit of the bottom factor was involved.
All that remains is a big addition problem, adding up rows c through g inclusive. Draw a line under row g as shown in figure 12, and start adding.
In any case, the result of the big addition is the result of the overall multiplication problem, as shown on row h of figure 12.
Let’s be super-explicit about the rules for keeping things lined up in columns.
It pays to think of the short-multiplication products in groups. The groups are labeled in figure 12. Row c is the “by one” group. Rows d and e form the “by twenty” group. Rows f and g form the “by three hundred” group.
The first rule is that each group is shifted over one place relative to the group above it. For example, the rightmost digit in row d is shifted one place relative to the rightmost digit on row c. Similarly, the rightmost digit in row f is shifted one place relative to the rightmost digit in row d.
This rule has a simple explanation: The groups inherit place value from the digit in the lower factor that gave rise to the group.
As another way of expressing the same rule: Each group is lined up under the digit in the lower factor that gave rise to the group. For example, in figure 12, the group on lines f and g is lined up under the 3 in the lower factor. Similarly, the 8 on line e is shifted over one place relative to the 10 on line d.
The second rule is that within each group, each short-multiplication product is shifted over one place relative to the previous factor in the group. For example, in figure 12, the 12 on line e is shifted over one place relative to the 14 on line d.
This rule also has a simple explanation: Each of the products inherits some place value from the digit in the upper factor that gave rise to the product.
Let’s do another example, as shown in figure 13, which illustrates one more wrinkle.
This example calls attention to the situation where some of the short-multiplication products have one digit, while others have two. You can see this on row c of the figure, where we have 3×3=9 and 3×8=24. In most cases it is safer to pretend they all have two digits, which is what we have done in the figure, writing 9 as 09. Similarly on line d we write 6 as 06. This makes the work fall into a nice consistent pattern. It helps you keep things lined up, and makes the work easier to check.
In some cases, such as 345×1 or 432×2, all the short-multiplication products have one digit, so you can write them all on a single line, if you wish. This is less work, and more compact. On the other hand, as discussed in reference 2, always remember: paper is cheap. You may find it helpful to write the short-multiplication products as two digits even if you don’t have to.If even one of the products (other then the leftmost one) requires two digits, you will almost certainly need two rows anyway, so you might as well get in the habit of using two rows.
Mathematically speaking, writing one-digit products as two digits is unconventional, but it is entirely correct. It has the advantage of making the algorithm more systematic, and therefore easier to check.
In any case, the result of the addition is the result of the overall multiplication problem, as shown on row g of figure 13. That’s all there is to it.
This algorithm ordinarily uses two rows of intermediate results for each digit in the bottom factor. In special cases, we can get by with a single row.
Another hallmark of this algorithm is that we first do all the short multiplying, and then do all of the adding. Every time we do a short multiplication, we just write down the answer. This has several major advantages:
Conversely, if any of the short-multiplication results looks suspicious, you can easily figure out where it came from, and re-check the multiplication.
This differs from the old-fashioned “textbook” approach, which uses only one row per digit, as shown below. The old-fashioned approach supposedly uses less paper – but the advantage is slight at best, and if you allow room keeping track of “carries” throughout the tableau, the advantage becomes even more dubious. Besides, paper is cheap, so it is penny-wise and pound-foolish to save paper at the cost of making the algorithm more complex, more laborious, and less reliable.
The old-fashioned approach may look more compact, but it involves more work. You have to do the same number of short multiplications, and a greater number of additions. It requires you to do additions (including carries) as you go along.
Last but not least, it makes it much harder to check your work.
| 4 | 5 | 6 | 7 | |||
| × | 3 | 2 | 1 | |||
| 4 | 5 | 6 | 7 | |||
| 9 | 1 | 3 | 4 | |||
| 1 | 3 | 7 | 0 | 1 | ||
| 1 | 4 | 6 | 6 | 0 | 0 | 7 |
The old-fashioned approach.
Not recommended.
As discussed in reference 2, always remember: paper is cheap. Being able to check your work is important; saving paper is not important.
The long-multiplication algorithm as presented here is guaranteed to work. That’s because it is quite directly based on the fundamental axioms of arithmetic, including the axioms of the number system.
Consider the numbers 4567 and 321 which appeared in section 3.1. We can expand 4567 as 4000+500+60+7. That’s what 4567 means, according to the rules of the Hindu number system. Similarly, we can expand 321 as 300+20+1.
The reason for expanding things this way is that in the sum 4000+500+60+7, each term consists of a single non-zero digit, with some place value.
The next step is to expand the product 4567×321 as (4000+500+60+7)×(300+20+1). We can then carry out the product in the expanded form, term by term, by repeated application of the distributive law. In our example, there are four terms in the first factor and three terms in the second factor, which give us 12 terms in the product, as shown in table 1. Each term in the product consists of a single-digit multiplication – a short multiplication – with some place value.
| 300 | 20 | 1 | ||||
| 7: | 2100 | 140 | 7 | |||
| 60: | 18000 | 1200 | 60 | |||
| 500: | 150000 | 10000 | 500 | |||
| 4000: | 1200000 | 80000 | 4000 |
So, the main thing the algorithm needs to do is to help you write down these 12 numbers in a convenient, systematic way.
One convenience is that the algorithm saves you from writing down all those zeros. You pay a small price for this. The price is that you absolutely must keep the numbers properly lines up in columns.
The rules about how to write the numbers in columns are not magic; they are just a way of keeping track of place value. They are a direct consequence of the axioms of arithmetic, including the axioms of the number system.
In particular, the “12” that appears in the lower-left element of table 1 is the same “12” that appears at the left of row g in figure 12 ... and the latter is lined up in columns so as to give it the correct place value.
The word “multiplicand” is more-or-less Latin for “the thing being multiplied”.
In figure 7, some people insist that the top number should be called the “multiplier” and the bottom number should be called the “multiplicand”. Meanwhile, other people insist on naming them the other way around. Quite commonly, they use the words in ways inconsistent with the supposed definition.
All of this is nonsense. Multiplication is commutative. Pretending to see a distinction between the two numbers is the silliest thing since the holy war between the Big-Endians and the Little-Endians.
Furthermore, multiplication is associative, so we could easily have three or more things being multiplied, as in 12×32×65×99, in which case it is obviously hopeless to attempt to distinguish “the” multiplier from “the” multiplicand.
The modern practice is to call both of the numbers in figure 7 the factors. You can equally well call both of them multipliers, or call both of them multiplicands. Along the same lines, modern practice is to say that an expression such as 12×32×65×99 is a product of four factors.
There are also holy wars as to whether 4567×321 means 4567 “times” 321, or 4567 “multiplied by” 321. The distinction is meaningless. Don’t worry about it.
Copyright © 2007 jsd