1  Pressure in Neutron Stars, Metals, Atoms, etc.

The big questions for today are:

• Why do neutron stars exist?
• Why is the speed of sound much higher in metals than in ideal gasses?
• Why do atoms not collapse and become 100,000 times smaller than they are?

In discussions of such issues, one hears a lot about “degeneracy pressure”. Similarly, in chemistry and condensed-matter physics, one hears a lot about the “exchange interaction”.

So, to make progress on the big questions, we need to understand:

A) What is this so-called “degeneracy” pressure, and

B) Should the exchange interaction be considered “fundamental” – on the same footing as the gravitational interaction, the strong nuclear interaction, et cetera?

Executive summary: There is nothing special about “degeneracy” pressure. It’s just pressure.

• A non-degenerate gas has pressure. It is compressible.
• A partially-degenerate gas has pressure. It is compressible.
• A degenerate gas has pressure. It is compressible.

The only halfway-special thing is that when there is degeneracy, the pressure will be different from what a naïve classical model would have predicted. For a Fermi gas, it will be higher. In particular, the pressure of a degenerate Fermi gas doesn’t go to zero at low temperatures.

This document is also available in PDF format. You may find this advantageous if your browser has trouble displaying standard HTML math symbols.

As the saying goes, learning proceeds from the known to the unknown. We can’t attack the aforementioned big questions until we have a clear idea of what degeneracy is, what pressure is, and why a fundamental force is called fundamental. Here are some smaller questions and answers that may serve as useful stepping-stones in preparation for answering the big questions.

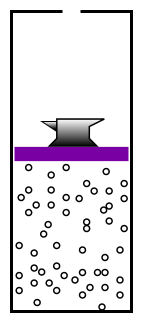
Question 0: In figure 1, why doesn’t the anvil descend all the way to the bottom? It would have lower gravitational potential energy there. The system should go to a low-energy state.

Figure 1: Anvil Supported by Piston

Answer: If the anvil went down, the microscopic kinetic energy of the gas molecules would go up. We have a name for this change in gas energy as a function of volume: It’s called pressure.

Question 1: Is this fundamental? Why is kinetic energy not included on the usual lists of “fundamental interactions”?

Answer: Kinetic energy is always part of the equations of motion. It is not listed as a fundamental interaction, because it is not an interaction. It is present even in the absence of interactions, including when there is only one particle, or when the particles are so far apart that they don’t appreciably interact. In some sense it is more fundamental than the so-called “fundamental interactions”.

See also item 12 below.

Question 2a: How big is a proton, a hydrogen nucleus?

Answer: about one Fermi, 10⁻¹⁵ meters.

Question 2b: How big is an electron?

Answer: zero. For purposes of atomic physics, an electron is a point particle. No structure.

Question 2c: How big is a hydrogen atom?

Answer: Roughly one Ångstrom, 10⁻¹⁰ meters in diameter. The atom is fluffy and squishy, so it’s hard to measure (or even define) “the” exact diameter, but this is a reasonable estimate.

Question 2d: What’s the electrostatic potential energy for an electron when it is about half an Ångstrom away from a proton?

Answer: About −29 eV (measured relative to a widely-separated electron and proton). You can calculate this directly from Coulomb’s law.

Question 2e: What’s the actual binding energy for the electron in a ground-state hydrogen atom?

Answer: One rydberg, 13.6 eV. This can be measured super-accurately by spectroscopy. It can also be calculated from first principles, if you know enough about atomic structure. This number is markedly less than the electrostatic energy mentioned in item (2d), because we have to take the kinetic energy into account. There’s a lot of kinetic energy.

Actually, we know via the virial theorem that the average potential energy should be −2 times the kinetic energy, for any 1/r potential. (This works for gravity, too.) Therefore the number in item (2d) is only an estimate. The actual electrostatic energy is two rydbergs, i.e. −27.2 eV. This tells us that in some appropriately-weighted average sense, the average electron-proton distance must be slightly larger than half an Ånstrom, but only very slightly. Half an Ånstrom is still a rather good estimate.

Question 3: Why isn’t the hydrogen diameter one Fermi instead of one Ångstrom? Why doesn’t the electron just spiral in and sit on top of the proton? It would have 10⁵ times more binding energy there. Answer: If you try to confine an electron to such a small volume, it’s kinetic energy would go up. Conceptually (and even semi-quantitatively) you can think of the hydrogen atom as an electron in a “container” with electrostatic forces pushing in from all sides. The electron-proton electrostatic attraction is like the anvil in figure 1, trying to make the container smaller, but it is opposed by the pressure of the electron-gas inside the container.

Question 4: In figure 1, if we lower the temperature of the gas, it shrinks. At zero temperature the anvil goes all the way to the bottom. Does question 3 imply that the size of the hydrogen atom should be proportional to temperature, too?

Answer: No. The kinetic energy of the atomic electron is essentially independent of temperature until you get to very high temperatures. At normal temperatures and below, the KE “levels off” at a value that depends only on the size of the box. This has got nothing to do with the electron’s charge; neutral particles such as neutrons and even photons behave the same way.

Question 5: How can we understand this “leveling off” of the low-temperature pressure in terms of high-school Newtonian mechanics?

Answer: We can’t. We don’t live in a Newtonian universe. We live in a universe governed by the laws of quantum mechanics. Get used to it.

Question 6: But how come we used one set of rules for question 0 and another set of rules for question 4?

Answer: We didn’t. Quantum mechanics gives the right answer for question 0 and question 4. QM always gives the right answer. Sometimes the classical approximation also gives the right answer, but that is just icing on the cake. In question 0, the compression of the gas can very accurately be described quantum-mechanically, in terms of shortening the wavelength of the wavefunction of the gas particles in proportion to the shortening of the region they’re in. See section 5 for details.

• You can demonstrate this very clearly with a gas of microwave photons. Start out with one liter of microwaves at 1 GHz and compress them down to half a liter at 2 GHz.
• You can demonstrate the key idea using a violin: Start with your finger near the nut, say A# on the A string. Pluck the string. Then slide your finger to shorten the active part of the string by a factor of two. You’ll hear the frequency go up an octave. The total energy of the vibrations will be increased, because you did work on them as you compressed them into the smaller region.

Remember: The quantum description is always right. The classical description is an approximation that is sometimes valid at high temperatures and low densities (and not necessarily even then). If you take any approximate law and extrapolate it beyond its range of validity, you’ll get fooled for sure.

Question 7a: How come you never told me this before?

Answer: You didn’t ask. If you do experiments in the regime where the classical approximation is valid, it’s hard to notice non-classical effects.

Question 7b: Why can’t you give me a simple classical explanation of degeneracy?

Answer: You’re specifically asking about a non-classical phenomenon. That’s what degeneracy means. So don’t be surprised if you get a non-classical explanation. If you’re allergic to bread and cheese and tomatoes, don’t order a pizza.

Question 8: Why is a sodium atom markedly larger than a neon atom, and why is its first ionization energy markedly lower?

Answer: Electrons are fermions. That makes their wavefunction slightly different from waves on a violin string. On a violin, you can excite the fundamental mode as much or as little as you want, over a very wide range. For electrons, you can’t do that. You can put at most two electrons in the fundamental mode (one spin up, one spin down) and at most two in the first partial, and at most two in the second partial, and so on. If you want to put a lot of electrons in a small box, you will have to occupy some pretty high-numbered modes. These have lots of momentum, so the zero-temperature pressure is higher than it would be for non-fermions. The valence electron in a sodium atom has so much kinetic energy that the nucleus can barely hold on to it.

You won’t notice this at high temperatures and low densities, because then you’re trying to put, say, hundreds of fermions into millions of modes, so you can always find an available unfilled mode for whatever you’re trying to do.

Question 9: What’s this got to do with neutron stars?

Answer: The analogy between neutron stars and atoms is rather tight. In one case, the central force is gravitational; in the other case it’s electrostatic. In one case the fermions are neutrons, in the other case they’re electrons. But the essential part of the story is the same: It’s a box full of fermions. The pressure is due to the momentum and kinetic energy, which has to do with wavelength.

Question 10: What does this tell us about non-metallic solids? In a solid object such as a sugar crystal, the atoms and molecules are sitting pretty much cheek-by-jowl (unlike a gas where there is plenty of room between the particles). Within each atom, the electrons are degenerate. If you try to compress the solid, you encounter a fair amount of degeneracy pressure. This explains why the speed of sound is higher in solids than in gasses.

Question 11: What does this tell us about metals? In a metal, you have a crystalline lattice of metal ions, which is by itself a solid and resists compression for the reasons discussed in the previous item. But in addition, in the metal you have the conduction electrons, which are highly degenerate, and exert their own “degeneracy pressure”.

Question 12: What does this tell us about the fundamental forces (gravitational, electroweak, and strong)?

Answer: Nothing. Particles have momentum and kinetic energy quite independent of which fundamental force(s) they interact with. And boson/fermion character is independent of the fundamental forces. If you’re trying put too many fermions into a mode, you can’t “force” them in there using a stronger “force”. It’s just not going to happen. They will either go into another mode or not go in at all.

Question 13: What if we redefine “kinetic” energy?

Oddly enough, that is possible. The definition of “kinetic” energy depends on what you take as “the” coordinate(s). Note the contrast:

If you look at an ideal gas microscopically, all the energy is KE.

If you put the gas in a cylinder and take the macroscopic position of the piston as the only coordinate of interest, the gas is like a spring,1 and there’s a potential energy ... in this coordinate system.

In classical canonical mechanics, there’s a formal symmetry. You can perform a change of coordinates that turns position into momentum, and momentum into position. That is, you can turn KE into PE and vice versa.

Be that as it may, if we stick to the usual coordinates for electrons and protons, the picture presented in this section is correct: the microscopic kinetic energy is the only thing that prevents atomic electrons from spiraling into the nucleus.

Bottom line: There’s nothing special about “degeneracy” pressure. It’s just pressure. The pressure in a degenerate Fermi fluid is higher than it would be in a non-degenerate or non-fermionic fluid under comparable conditions of density and temperature ... but it’s just a difference in quantity, not a difference in kind. The most remarkable thing is that the pressure doesn’t go to zero at low temperatures.

2  Annihilation, not merely a Node

What we know about interference patterns is partially but not entirely helpful in explaining the annihilation of the wave function when two fermions try to get into the same state. Let’s compare the two ideas: In the left column we discuss an interference pattern, and in the right column we discuss exclusion:

In a many-body problem there is such a thing as the vacuum state, representing the state where there are zero particles. Call it |vac⟩. It’s a perfectly good state. Now, if you apply the same creation operator twice (starting from that state or any other state) the result is not |vac⟩, the result is nothing at all. The unstate. Zilch. Not |vac⟩ but 0.0 |vac⟩, which is not at all the same.

3  Classifying Interactions as “Fundamental” Or Not

Note: It is preferable to speak of fundamental interactions rather than fundamental forces.

The current canonical list of fundamental interactions is:

• The electroweak interaction, which comprises
  • electric fields,
  • magnetic fields, and
  • the weak nuclear interaction.
• The strong nuclear interaction.
• Gravitation.

At present we have no good way to explain any of these interactions in terms of the others, nor to explain them in terms of some more-fundamental description – although efforts continue in this direction. So for now at least, these are considered distinct and equally fundamental.

The list changes from time to time. In the middle of the 19th century, electrostatics and magnetostatics were considered distinct and fundamental. Later they came to be seen to be special cases of the unified, more-fundamental electromagnetic interaction, which claimed a place on the top-level list, demoting electricity and magnetism to sub-items. Similarly, when the weak nuclear interaction was first discovered, it was considered distinct and fundamental, but later it (along with electromagnetism) was seen to be a special case of the more-fundamental electroweak interaction, which claimed a place on the top-level list, demoting the weak interaction to a sub-item.

Pressure might have been on the list in the early 19th century, but it was stricken when people realized it can be fully explained in terms of the other items on the list, via “kinetic theory”. The idea of degeneracy arose much later, so there was never the slightest chance that the pressure of a degenerate gas would be considered a fundamental interaction.

The gravitational interaction is a field. It has dimensions of force per unit mass. Pressure is also a field. It has dimensions of force per unit area, or (equivalently) energy per unit volume. The question is not whether there’s a force due to pressure; the question is whether it’s fundamental. It’s not. It’s merely a consequence of the known fundamental laws.

By way of analogy: skin-friction drag on an airplane is also a force. No doubt about it. But it’s not fundamental. It’s merely a consequence of the known fundamental laws.

4  Gravity “Overcoming” Pressure, Or Not

One sometimes sees statements such as “a neutron star doesn’t collapse because gravity cannot overcome the degeneracy pressure”.

That’s true except when it’s not true. It is highly overstated, and highly open to misinterpretation.

By way of analogy: There are some books resting on my coffee-table. You might say they don’t fall to the floor because gravity “cannot” overcome the upward pressure that the coffee-table exerts on the books. But:

• “Cannot” is too strong a word, creating an overstatement that is not entirely true.
• If/when gravity does not overcome the pressure, it is just a consequence of the prosaic laws of physics – it is not a new 11th commandment that supersedes the other laws of physics.

If I pile more and more books onto the coffee-table, eventually the table-legs will buckle, and the whole pile will collapse onto the floor.

The story for neutron stars is entirely analogous: Gravity does not overcome the pressure of the neutron gas, except when it does. If you start with a neutron star that is stable against collapse, and pile more and more material onto it, eventually it will collapse. There is no such thing as degeneracy pressure; there is just pressure. It is just a consequence of the prosaic laws of physics – it is not a new 11th commandment that supersedes the other laws of physics.

5  Gas Pressure

Let’s calculate the pressure in a gas. It’s easy. A more-detailed calculation can be found in reference 1, but we can sketch the outline here. We start with the definition of pressure,

where E is the energy, V is the volume, and S is the entropy. For a definition of entropy, see reference 2.

We begin by (temporarily) assuming that when we change the volume, the exact same quantum states are occupied before and after the change. For details on this, see section 8. This is more than sufficient to guarantee constant entropy.

Consider a particle in a cubical box of size L so that V = L³. The lowest-lying state has wavevector k = [1,1,1] π / L. A generic state has wavevector k = [n_x, n_y, n_z] π / L, where 1+n_x is the number of nodes in the wavefunction in the X-direction. The state has momentum p = h k / 2π. For a nonrelativistic particle of mass m, the kinetic energy is KE = p²/2m.

The energy of the gas as a whole is

where the sum runs over all occupied states. We can write this as

where α depends on which states are occupied. We could do the sum to obtain an exact expression for α, but that would just be a distraction from the essential L-dependence of equation 4. For present purposes, all that matters is that α is independent of V and independent of changes in V, assuming gradual changes (of the kind defined in section 8). Then we have

Hence

where γ is called the adiabatic exponent. It is sometimes called the compressibility index but that’s a misnomer; we would be better off calling it the stiffness index since large γ means the gas is hard to compress. (It is also called the ratio of specific heats for reasons that need not concern us here.) We have calculated that γ = 5/3 for a gas of nonrelativistic pointlike particles.

Note that γ does not depend on whether the gas is degenerate or not! The calculation is valid for a non-degenerate non-Fermi gas such as helium, and equally valid for a degenerate Fermi gas such as the electrons in a white dwarf, or the neutrons in a neutron star.

For a gas of relativistic pointlike particles, the kinetic energy is KE = pc so there is only one factor of L in the denominator of equation 4. Therefore the energy goes like V^−1/3 and γ = 4/3.

It is evident from equation 4 that for a nonrelativistic gas, the energy (and hence pressure) depend inversely on the mass of the particles. A gas of N electrons in a box of size L will have a much higher pressure than the same number of neutrons in a same-sized box. The neutron pressure in a neutron star is higher than the electron pressure in a white dwarf – but that is in spite of, not because of, the mass of the particles; it is because the particles have been stuffed into a box that is orders of magnitude smaller, roughly 10 kilometers rather than thousands of kilometers.

6  Collapse

Consider the following analogy:

To understand how a white dwarf turns into a neutron star we need to rescind the assumption discussed in section 8. That is, we rescind the assumption that compression results in corresponding states. At some point, when the gravitational force is large enough, the easiest way to compress the star is to get rid of some electrons, combining them with protons to make neutrons. (Neutrinos are produced, too, but they escape.) Once this process starts, the star contracts, with a really small γ. The gravity is everywhere stronger, with no countervailing increase in pressure, so the process accelerates. Boom. Supernova.

Pulsations are unstable if the increase in gravity (due to an increase in density) is greater than the increase in pressure (due to the same increase in density). According to reference 3, for Newtonian gravity, the criterion is γ = 4/3, so stars are stable as long as the gas is nonrelativistic, and marginally stable even if the gas is relativistic. However, the derivation of this result appears to rest on some questionable approximations, and it wouldn’t surprise me if Newtonian gravity produced instability when the gas is sufficiently relativistic. Real gravity (general relativity) is slightly stronger than Newtonian gravity, so at some point gravity wins.

7  Quantum Fluctuations and Thermal Fluctuations

Figure 2 shows the energy as a function of temperature of a harmonic oscillator in thermal equilibrium. In the classical approximation, the energy is equal to 1kT, as shown by the magenta line. The true (i.e. quantum mechanical) result is shown by the heavy dark line. You can see that at high temperatures, the true behavior closely tracks the classical approximation, while at low temperatures the true energy bottoms out at ½ℏω, which is the so-called “zero point energy”.

The curve in figure 2 is not an artist’s conception; it is a quantitative graph of the function

You can easily verify that this function behaves as described, by considering the behavior of coth(x): for large x it goes to 1, and for small x it goes like 1/x.

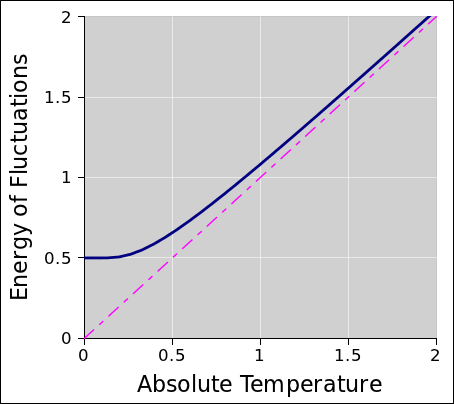Figure 2: Fluctuations versus Temperature

It is worth remembering that this one function describes the thermal fluctuations and the quantum fluctuations. Indeed, it does not distinguish them, especially not near the “knee” in the curve in figure 2. The notion of “purely quantum” fluctuations and “purely thermal” fluctuations are just names we give to the two limiting cases.

8  Appendix: Corresponding States

We have been considering a process that changes the size of the box (L) but leaves the quantum numbers n_x, n_y, and n_z unchanged. The “before” state and the “after” state will not be geometrically congruent, because the size has changed. However, the two states will be related by a very simple topological distortion. The wavelength will be different, but the quantum numbers n_x, n_y, and n_z will be the same.

You can show, using time-dependent perturbation theory, that this is indeed how a gas behaves, provided the volume-change is gradual enough, and no chemical reactions or nuclear reactions are taking place.

I like to call this the corresponding-states approximation, which is a nice descriptive name. It is sometimes called the Born-Foch approximation. You can call it simply the gradual approximation, if you assume there are no chemical reactions or nuclear reactions taking place.

More commonly it is called the adiabatic approximation. However, that is in some ways a trap for the unwary, because it conflicts with other, older, and more-common definitions of the word “adiabatic”.

Important note: The formulas that we have derived give a correct description of what happens for any isentropic process, whether it is gradual or not – but we haven’t actually proved that.

*   References

1.

John Denker,
“The Laws of Thermodynamics”
www.av8n.com/physics/thermo-laws.htm

2.

John Denker,
“Entropy” – Chapter 2 of Modern Thermodynamics
www.av8n.com/physics/thermo/entropy.html

3.

Misner, Thorne, Wheeler,
Gravitation

1

The “air spring” is even more closely analogous to a regular mechanical spring if we use a double-acting piston, with high-pressure gas on both sides of the piston. This allows the air spring to have a well-defined natural length, and a well-defined spring constant for small excursions relative to the natural length. Similar good results can be achieved by using a single piston plus a mechanical linkage that prevents unlimited expansion.