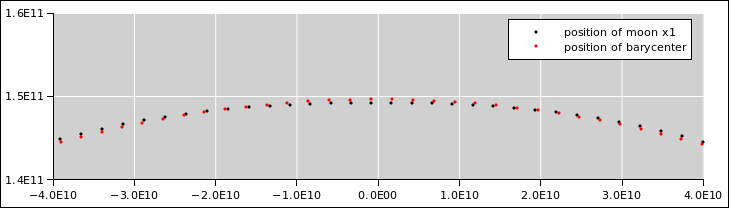
Figure 1: Moon’s Orbit in Absolute Space
Each month, the moon goes around in its orbit. Specifically, it orbits around the center-of-mass of the earth/moon system.
The same goes for the earth: As you might expect based on the third law of motion, the earth also orbits around the center-of-mass of the earth-moon system.
Let’s take a moment to figure out where the center-of-mass is. It is convenient to use the radius of the earth as our measuring stick. The center-to-center distance between the earth and the moon is about 60 times the radius of the earth (reference 1). The radius of the moon is about 1/4 the radius of the earth. We don’t actually need that, but it gives us an amusing consistency check: You know just by looking that the diameter of the moon subtends half a degree as seen from earth. You can easily verify that this is consistent with the given size and distance numbers.
You might guess that the mass of the moon would be (1/4)3 of the mass of the earth, if the densities were the same, but in fact the moon is only about 60% as dense, so the mass ratio is more like 0.0123 or about 1 part in 81. Since 81 is bigger than 60, the center-of-mass is below the surface of the earth. However, it’s not much below; it is considerably closer to the surface than it is to the center. Specifically, it is 73% of the way from the center to the surface.
Here is a movie that shows how it works. The green crosshairs are centered on (and comoving with) the center-of-mass of the earth/moon system. We are looking down on the ecliptic plane. The white splotch on the top of the rotating planet is the north polar ice cap. The north pole is near the middle thereof. Once a day, the earth rotates around its axis. I have speeded things up by a factor of 86400, so that one solar day in the simulated world is represented by one second of our time as we watch the movie.
Once per sidereal month, the center of the earth orbits around the center-of-mass. The gray arrow points toward the moon. The moon doesn’t fit in the frame; remember that it is 60 earth radii away.
The fact that the moon orbits around the center-of-mass (not exactly the center of the earth) has some interesting ramifcations. For one thing, suppose you wanted to calculate the force needed to keep the moon in its orbit:
| (1) |
and compare that with the force provided by gravity:
| (2) |
You have to be careful, because the little r in equation 1 is the distance to the center-of-mass, whereas the big R in equation 2 is the whole center-to-center distance. The difference is enough to be noticeable, especially when you consider how accurately such things can be measured.
In the movie, the stars in the background are not true to life. They are just the proverbial artist’s impression. In this case they are randomly-distributed dots. It would be straightfoward to fix this, by dipping into the HYG database and plotting the relevant stars near the South Ecliptic Pole. If anybody wants to implement this, or make any other upgrades, the source is available (reference 2).
If you want to orient the diagram against real stars, the constellation Pisces is far off the right side of the diagram, the Gemini / Taurus border is far off the top of the diagram, Virgo is far off the left, and Saggitarius is far off the bottom.
Gemini
Taurus
Cancer
Aries
Leo
Virgo ... Pisces
Libra Aquarius
Scorpio Capricorn
Saggitarius
The start of the simulation corresponds to the spring equinox, March 20th, with the sun in Pisces. Two months later, the sun is in Taurus.
The astute observer will notice that the earth rotates 361 degrees per day, not 360. This is because our “day” is the conventional solar day (not the sidereal day), yet the video uses a sidereal frame of reference.
In previous sections, we used a non-inertial reference frame, namely one that followed the earth/moon center-of-mass in its annual orbit around the sun.
Here’s an interesting question: Is the moon’s orbit always concave toward the sun? The answer is not entirely obvious. In fact it’s a close call.
The answer turns out to be yes, but just barely. When we consider the gravitational acceleration of the moon, the contribution from the earth is smaller than the contribution from the sun ... but it’s smaller by a factor of 2.2 or so, which is not a very large number.
It’s super-easy to calculate this number; it’s the ratio of the masses divided by the square or the ratio of the distances.
In particular, if we ask the same question about the space station or anything else in low earth orbit, we get the opposite answer: During part of its orbit, the space station is very definitely moving away from the sun.
It’s hard to draw a diagram of what the moon is doing. That’s because if we zoom out far enough to see the curvature of the earth’s orbit, the earth/moon distance is too small to be easily seen. Conversely, if we zoom in close enough to see the earth/moon relationship, the curvature of the earth’s orbit is too slight to be easily seen. In figure 1 we try to split the difference. The dots in the figure are spaced one day apart.
It must be emphasized that figure 1 is accurate. In contrast, figure 2 is misleading because it exaggerates the earth–moon distance by a factor of 8. This makes it look like the moon spends part of its time moving away from the earth ... when in fact it doesn’t.
Note that exaggerating things by a factor of 8 is not enough to make a qualitative change in the depiction of velocity, but is enough to mess up the depiction of acceleration.
A better way to visualize the situation is shown in figure 3. That is, we display the acceleration vector directly. You can see that it always points in the general direction of the sun, although the magnitude and direction are significantly perturbed by the earth’s field.
As always, a vector has a magnitude and a direction ... but not a location. You can arbitrarily change the location of a vector without changing its meaning. However, in figure 3 we employ a rather common dirty trick: The lines encode both the acceleration of the moon and the location of the moon. That is, the line is more than a vector. The line is drawn with one of its ends sitting on the location of the moon. As a separate matter, the length and direction of the line encode the acceleration vector.
The spreadsheet used to prepare this figures is available (reference 3).