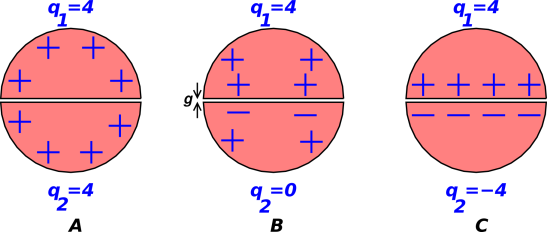
Figure 1: A Capacitor, with Charge and Gorge
When people speak of “the amount of charge” in a battery or capacitor, usually it is a misnomer, of the kind that leads to serious misconceptions. It would be better to call it the gorge, and to speak of gorging and disgorging the device. Charge is something else.
In particular, charge is strictly conserved, but gorge is not. A real battery has some finite shelf life, and a real capacitor has some nonzero internal leakage. The battery just sitting there will disgorge itself. It would be a tremendous mistake to think that “charge” is being lost, because that would violate conservation of charge.
Consider the situation shown in part A of figure 1. We have a sphere that carries a charge of +4 units on the upper hemisphere and another +4 units on the lower hemisphere. Presumably there is – somewhere – a counter-charge of −8 units, but we assume it is so far away that the details don’t matter. The sphere has been cut along the equatorial plane, so that that there is a tiny gap of size g between the upper hemisphere and the lower hemisphere. However, for present purposes the gap doesn’t matter very much. Basically what we have is a sphere with a total charge of +8 units.
We now turn to part B of figure 1. As before, there is a charge of +4 units on the upper hemisphere ... but now there is zero charge on the lower hemisphere. We assume the gap is so small that the mutual capacitance between the hemispheres is enormous compared to the self-capacitance. We can figure out (by symmetry or otherwise) that the 4 units of charge will distribute themselves evenly over the sphere. In the far field, the field exhibits (to leading order) a monopole field pattern, which is what we would expect from +4 units of charge. There will also be a dipole term, due to the voltage difference between the two hemispheres, but in the far field, compared to the monopole term, the dipole term will be negligible. We can understand this as follows: There will be a significant field in the gap, but because the gap is small the mutual capacitance is large, so the voltage difference between the hemispheres will be small.
Finally, we turn to part C of figure 1. As before, there is a charge of +4 units on the upper hemisphere ... but now the charge on the lower hemisphere is −4 units. In the far field, this looks like a dipole. It won’t be a very strong dipole, because the separation between the positive and negative charges is not large, but in the far field this small dipole term is all there is.
Now we get to the tricky part. Consider the following contrast:
The problem is, the word “charge” is being used in two inconsistent ways. To solve this problem, let’s define the gorge, G, so that
| (1) |
Now we can unambiguously say that in part C of the figure, the object has zero units of charge and four units of gorge.
Meanwhile, in part B we have four units of charge and two units of gorge. In part A we have eight units of charge and zero units of gorge.
The mapping in equation 1 can be reversed as follows, as you can easily verify:
| (2) |
Note that according to the laws of physics, the charge Q is conserved. Specifically, Q obeys a strict local conservation law. In contrast, gorge is not conserved. Not at all. If you put many units of gorge on a capacitor – or a battery – and come back later, you might find that all of the gorge has disappeared, due to some internal leakage process.
Note that what we have here is just a special case of the three-terminal capacitor: The upper hemisphere, the lower hemisphere, and the far-away counter-electrode. The terminology of charge and gorge is not particularly good for handling three-terminal capacitors in general ... but the case we have considered here is so exceedingly common that it is worth having special tools for handling it.
The concept applies equally well to batteries as well as capacitors. In real-world situation, the total charge Q might be 10 or 12 orders of magnitude smaller than the gorge G. In such a situation the total charge Q is sometimes called “stray” charge. As another way of saying more-or-less the same thing: In normal operation, to an excellent approximation, you have have a current flowing “into” a capacitor; instead you have a current flowing through a capacitor, i.e. in one terminal and out the other.
The concept of gorge is used in reference 1, reference 2, reference 3, reference 4, and reference 5.