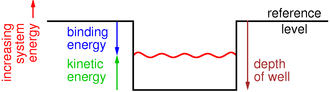
Figure 1: Binding Energy ± Kinetic Energy
There are quite a few things we know about mass. I will present them in two separate lists. The first list consists of if-and-only-if propositions. For example, if you know m, you can use it to predict the ratio ps/v (where ps is the momentum and v is the velocity) ... and conversely if you don’t know m, you can calculate it from ps/v.
| m2 c4 = E2 − ps2 c2 (1) |
where m represents mass, E represents energy, and ps represents the ordinary 3-vector momentum. For an explanation of where equation 1 comes from, see reference 1. (The “s” in ps stands for spatial, to distinguish ps from the energy-momentum 4-vector p.) If we choose units of measurement such that c=1, we can rewrite that as
| m2 = E2 − ps2 (2) |
| Erest = m c2 (3) |
where Erest is called the rest energy. The famous equation
| E = m c2 (at rest) (4) |
must be understood as a shorthand for equation 3. Einstein expressly intended equation 4 to apply to particles at rest.
According to modern ideas and modern notation, m is frame-independent, while the total energy E is just one component of a four-vector, and cannot be frame-independent. See section 4.
| p = m u (5) |
where p is the four-vector momentum, u is the four-vector velocity (u := dx/dτ), and τ is the proper time. A similar expression, valid to first order, can be written as:
| ps = m v (6) |
where ps is the three-vector momentum (the spatial part of p), v is the three-vector velocity (v := dx/dt), and t is the time in your chosen reference frame. (Beware: although ps is exactly the spatial part of p, v is not the spatial part of u. The latter are equal to first order, but not in general. See reference 2 for more about the relationship between reduced velocity and 4-velocity.)
| KE = .5 ps2 / m (7) |
where as before ps is the ordinary 3-vector momentum. This equation is valid to second order in v/c, as you can immediately verify by expanding equation 1 to lowest order.
It is amusing that relativity tells us what the non-relativistic result must be.
| F = m a (8) |
which is a corollary of item 3 if you define “force” in a way that is consistent with your definition of acceleration.
Note: Items (1) through (4) are equivalent to lowest order (or better), if you believe in special relativity.
| Fg = G M m / r2 (9) |
which is valid provided the gravitation is not too strong and not too rapidly changing. (In contrast, in general relativity, mass is not the only source of the gravitational field. For a simple demonstration that mass is not the whole story, see reference 3.)
I suppose it is somewhat a matter of taste, but I find it pointless and unhelpful to try to axiomatize physics. I care about knowing useful ideas, and knowing their limits of validity. You can choose any of the items on this first list as “the” definition of mass. I don’t care.
Now we come to the second list. These are if-then propositions. As an example of what I mean by that, if you are dealing with mass (in a non-relativistic situation) then you know it obeys a local conservation law. But the converse doesn’t hold; there are lots of things (e.g. electrical charge) that obey a local conservation law that have nothing to do with mass.
I consider the weak equivalence principle to be true but not axiomatic. (If it were axiomatic, Eötvös experiments would be impossible, or at best a waste of time, which is not what I believe.)
Indeed you have to be careful how you state the equivalence principle, lest you say something that’s not true. Recent experiments (reference 4) have measured the Lense-Thirring “frame-dragging” effect, which is due to non-Newtonian components of the gravitational field, components that cannot be described as an acceleration. These components are to plain old gravitation as magnetism is to electrostatics.
On the other hand, the equivalence principle has been tested experimentally to high accuracy. The last time I checked, it was good to one part in 1012, and there were plans afoot to check it to one part in 1015.
The restriction to table-top situations excludes nuclear reactions. It means that insofar as chemical reactions change the binding energy, this contributes a negligible amount to the overall mass. This is not exact, and it is not a law of nature; mostly it defines what we mean by “chemical” reaction (as opposed to nuclear reaction).
I emphasize that the relationship between mass and “amount of stuff” is an if-then relationship, not an if-and-only-if relationship. For example: if you understand mass, then you can use it as a measure of the “amount of stuff” ... but the converse does not hold. By way of counterexample, many products are sold by volume, using volume as a measure of “amount of stuff”. It works reasonably well for homogeneous substances, but not in general. For example, try adding one cup of milk to one pint of blueberries. The “amount of stuff” – measured by volume – is not additive.
For this reason we say that mass gives us a more robust notion of “amount of stuff”, in contrast to volume which is less robust.
Some people try to define (or at least describe) mass in terms of density times volume. At best this only works for homogeneous substances. Furthermore, it’s never a good idea to try to define a more-robust notion in terms of a less-robust one.
Items on the second list cannot be used as the definition of mass. Instead, they are very useful for broadening and deepening the understanding of mass, once an initial understanding has been established using some idea(s) from the first list.
Mass is somewhat of an abstraction.
In particular, it would be going too far to define mass in terms of what any particular instrument indicates. The instrument might be non-ideal, or it might be broken. In particular, if the instrument does not uphold the additivity principle (item 10) then we know something is wrong. As a specific example, an ordinary laboratory balance is non-ideal, in that you must add a correction for buoyancy. I do not believe that helium balloons have negative mass.
Meanwhile, I would not be comfortable going to the opposite extreme and saying that our notion of mass is independent of how we measure mass. It is pointless to ask what would happen if we couldn’t measure mass, because the fact of the matter is that we can measure mass. Using the ideas enumerated above, plus some engineering skill, we can devise quite a number of methods for measuring mass (relative to some standard) more or less accurately, more or less directly. If done right, all these methods are equivalent.
Perhaps we can benefit from an idea from high-school geometry. They explicitly designate points, lines, and planes as undefined quantities. These terms acquire meaning solely from the way they are used in the axioms of geometry. Trying to define “mass” in a few words is almost as unhelpful as trying to define “point” in a few words. You can perhaps equate mass to relativistic energy (item 1), but then you have to define energy, which is no easier. It is so fundamental that it is not easily defined in terms of more-fundamental quantities.
In section 1, we said the mass of a compound object is the sum of the mass of the constituents, corrected for binding energy. Sometimes people wonder whether there should also be a correction for the kinetic energy of the relative motion of the components (where by relative motion we mean the motion relative to the center of mass of the combined object).
The answer is that kinetic energy is important, but I didn’t mention it previously because I meant for it to be included in my definition of binding energy. To see how this works, consider the energy of a particle in a box. The particle is bound to the box.
Figure 1 shows the energy diagram for a particle in a square-well potential. In all such diagrams, the total energy increases upwards. In particular, the potential energy, as shown by the black line in the figure, increases upwards. Similarly, kinetic energy increases upwards. When the particle is within the square well, the system energy (shown in red) lies above the bottom of the well by an amount equal to the kinetic energy.
Beware that it is conventional to measure binding energy downward relative to the chosen reference level. This makes sense from the point of view that “more” binding means a “more negative” energy ... but it is a notorious trap for the unwary, because it is upside-down relative to the other energy-like quantities.
It is usually convenient (but not absolutely mandatory) to choose the reference level to correspond to an unbound particle (outside the well) at rest (no kinetic energy).
You can measure the binding energy directly, or equivalently you can start with the total depth of the well and then add a correction for the kinetic energy. These are two ways of calculating the same thing.
According to modern notation, m stands for mass.
According to modern terminology, “the” mass of a particle does not depend on the speed of the particle. It is redundant but harmless to say that m is the “rest” mass or the “invariant” mass.
| It is possible to define a speed-dependent mass, and to state the laws of physics in terms of this speed-dependent mass … but this is not recommended. See reference 5 for more about the history and status of this idea. | The modern practice is to express the laws of physics in terms of m, which we call “the” mass, and which is invariant. The laws (and the ideas) are simpler when expressed in terms of m, the invariant mass. |
| It is sometimes said that a fast-moving particle exhibits a larger resistance to acceleration, and therefore should have a larger mass, in accordance with equation 8 … but this is not recommended. | The modern practice is to say that the 3-acceleration is smaller than the 4-acceleration by a factor of gamma cubed, for reasons having to do with the geometry and trigonometry of spacetime, and having nothing to do with mass, as explained in reference 2. |
You can see from the basic properties of 4-vectors that the m that appears on the LHS of equation 1 is a Lorentz scalar, since the RHS is the dot product of a 4-vector with itself. Note that equation 1 is completely general, while equation 4 applies only if we measure an object’s energy (E) in a frame where the object is at rest.
For a discussion of how the feeling of weight arises, see reference 6. For details on how to define weight, see reference 7.
Anecdote:
When I was seven or eight, we visited the Old Tucson movie studio. They had an old-time railroad car sitting there. For a joke, my kid brother and I posed as if we were pushing the railroad car, grunting and grimacing. Somebody said “that’s ridiculous” ... which we took as a challenge. So we spent the next several minutes pushing really hard. It turns out that railroad cars have very good bearings. If a couple of kids push for long enough, they can pour a huge amount of momentum into the thing. For several minutes, nobody paid any attention to us. Then my mother noticed what was happening and said “Hey, where are you going with that railroad car?”
This got our father’s attention, and he was appropriately horrified. By this time the car was moving right along. It wasn’t moving very fast, but it was definitely moving, and showing no signs of stopping.
We ran around to the other end and the two of us, plus our father, pushed on it in the opposite direction. It took a long time to get it stopped.
It might be good to let all physics students try their hand at this kind of experiment ... with suitable safety precautions. You don’t need a railroad car; an ordinary automobile will do. Set up the car on a deserted stretch of level pavement, put it in neutral, and let people (a) push to get it rolling, and (b) pull in the other direction to get it stopped. Note that for part (b) I recommend pulling using ropes, to reduce the risk of anyone falling under a wheel. Attach the ropes to a strong point on the frame of the car (not to the bumper, since modern “energy absorbing” bumpers are surprisingly easy to damage). Also I recommend putting a driver in the car, who can apply the brakes if things start to get out of hand. Beware that the power brakes won’t have any power, so the driver will have to stomp on the brake pedal.
To get the car going, you have to push rather hard for a rather long time, because it is so massive. But if you keep pushing, you can get it going pretty fast. And then it will take a goodly amount of pulling to get it stopped.
There is a version of this experiment you can do indoors, using a cart. Use a big, robust cart that can carry 100 kg or so. Push it sideways back and forth. Compare the unladen cart (10 kg or so) to the laden cart (100 kg or so). This is worthwhile, but not nearly as impressive as the full size car (1000 kg or so).
The words that go with this lesson are that the weight of the car is irrelevant (to an excellent approximation), because the weight is canceled by the upward force of the road on the wheels. Meanwhile, the mass is still there. The inertia is still there. If you wanted to push the car along an equally-horizontal road on the moon, it would require just as much pushing. The weight would be 6x less, but the weight would still be irrelevant. The mass – the inertial mass – is the main thing you are feeling when you push it horizontally. (There is also a little friction, but not much, because the tires and wheel-bearings are designed to have very low friction.)
Another advantage of this demonstration is that it gives students a feeling (literally) for orders of magnitude. Toss a US nickel coin more-or-less horizontally from hand to hand: This is what 5 grams feels like. Shove on the car: This is what a megagram feels like.
Even in the zero-Gee environment of a space station, objects are weightless but not massless.
If you have a one-ton object in orbit and you want to set it in motion, you will have to push on it pretty hard for a pretty long time. (You also need something to push against, but that’s another story.) The amount of push (formally called impulse) is just the same as it would be for horizontal motion of a one-ton object on earth, such as the car discussed in section 5.1.
It is an interesting challenge to design a mass-measuring instrument that will work in a weightless environment.
The conceptual structure is clear: we have at least ten major ideas, all of which are true, and all of which are intimately related.
The question arises, in what order should these ideas be presented? There are ten-factorial possible ways of re-ordering these ideas. I see no physical reasons for declaring any of these ideas to be “the” natural starting point. There may be pedagogical reasons for choosing one starting point instead of another, but the choice will require tradeoffs and will be sensitive to personal preferences and other ill-defined details of the situation.
Bottom line: We know quite a few things about mass. They are deeply related. They are all important. They all need to be covered, but the order in which they are covered is largely a matter of taste. Asking which is “the” fundamental notion of mass is pointless and unphysical.
Thanks to Michael Edmiston and Hugh Logan for helping to clarify my thinking about these issues.