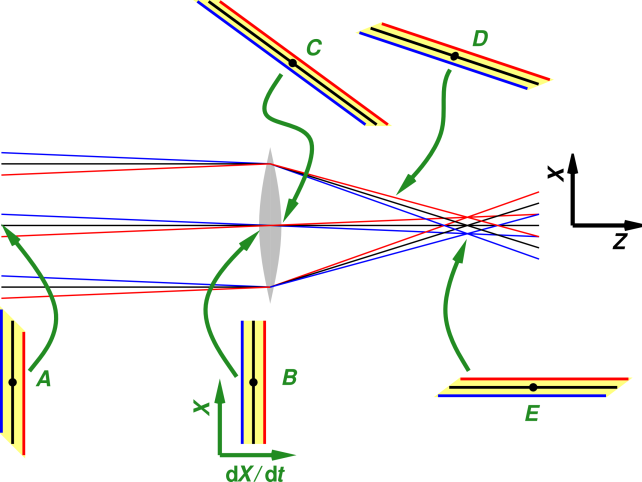
Figure 1: Thin Lens: Ray Tracing and Phase Space
We can start the discussion with the following assertion: It is not ever possible to focus the sun’s rays to a single point.
This statement is hard to prove. Examples won’t suffice. It can, however, be seen as an immediate consequence of Liouville’s theorem, which states that phase space is conserved.
There is an important physics lesson here. The fundamental importance of Liouville’s theorem beggars description.
For more discussion of Liouville’s theorem, including phase-space diagrams, see reference 1.
As an illustrative example, let’s consider the geometry shown in figure 1. Let our Z axis be the line between the middle of the sun and the middle of the lens. The sun is located far, far to the left of the diagram. The red rays in the diagram are coming from the west limb of the sun, while the blue rays are coming from the east limb of the sun, and the black rays are coming from the center.
For clarity, the figure exaggerates the angular size of the sun, showing it as 5 degrees instead of the actual 0.5 degrees.Also, for simplicity, we make the paraxial approximation; that is, we assume all rays are nearly parallel to the Z axis. This implies that the focal length is not unduly short compared to the diameter of the lens ... or, to say the same thing, the f/stop is not too small, and the numerical aperture is not too large. Therefore we can gloss over certain nonlinearities, especially the distinction between d/dt and c d/dZ.
We also make the sensible assumption that the sun is much larger than our lens, and very far away. Finally, we assume that the lens is large enough (compared to the wavelength) that diffraction effects are negligible (compared to the size of the image).
The aperture of the lens extends in the X direction from +D/2 to −D/2 for a total aperture of D. For simplicity we suppress the Y dependence for now; it is straightforward to add it back in.
We are concerned with a certain parcel of phase space. The parcel is shown as a yellow parallelogram in the figure. The parcel’s shape changes as a function of Z.
One axis of our phase space is X, and the other axis is dX/dt. Just in front of the lens, at point B in the diagram, the parcel has a particularly simple rectangular shape. The parcel extends in the X direction from +D/2 to −D/2. Its extent in the dX/dt direction is θ, where θ is the angle subtended by the sun, i.e. about half a degree.
To repeat, just in front of the lens, our phase-space parcel is a rectangle of size D times half a degree.
To construct the rest of the diagram, we need to consider two types of propagation, namely propagation through free space and propagation through a lens. In each case, we need a rule for what happens to each coordinate in phase space, i.e. a rule for what happens to X and a rule for what happens to dX/dt.
Minor point: Note the remarkable symmetry between the two laws: One involves position-change in proportion to momentum, while the other involves momentum-change in proportion to position.
Another minor point: Note the remarkable symmetry between the entrance to our optical system (point A) and the focal point (E). In the former case we the red rays have definite slope dX/dZ that is independent of the position X, while in the latter case the red rays have a definite position X that is independent of the slope dX/dZ. (Ditto for each of the other color-coded rays.)
Let’s consider another optical system, a two-lens system, basically a simple telescope.
In this section we take the momentum axis to be dX/dZ rather than dX/dt, so the axes in phase space are X and dX/dZ. The equations of motion are simple:
In each of the following figures, the blue shaded area represents the phase space at a certain stage, and the black arrows represent change the necessary to reach the next stage.
We see that the update of X is independent of X, and the update of dX/dZ is independent of dX/dZ. This is sufficient to guarantee that area in phase space is conserved. It is also sufficient to guarantee that the system is reversible. See also reference 2.
It is an easy and amusing exercise to show that for any thin lens, phase space is conserved. This is a consequence of the two propagation laws given at the end of the previous section. Each of the laws causes shearing of the parallelogram, and shearing can never change the area.
As an application of this idea, consider a zoom lens (i.e. an optical system with constant aperture but variable focal length). If you choose a larger focal length, you get a larger image of the sun (larger extent in X), and the rays from the lens will hit the image plane with a smaller range of angles (smaller extent in dX/dt). So once again, phase space is conserved.
Conservation of phase space is independent of the conservation of energy. Neither is a direct consequence of the other.
As for focusing the light of the sun: Based on the discussion so far, you might think you could take all of the solar energy entering the lens and focus it on an arbitrarily small spot, thereby achieving an arbitrarily high temperature. Well, you can’t. Conservation of energy does not forbid it, but conservation of phase space (along with some other basic laws) does forbid it. Long before you achieved a spot that small, you would be violating the paraxial approximation. More to the point, if you do the full analysis, you would find that forming such a small spot would require impossibly large values of dX/dt (greater than c).
Not coincidentally, such a tight focus would also violate the second law of thermodynamics. If you could focus the sun’s rays more tightly than permitted by Liouville’s theorem, it would be possible to create a focal spot hotter than the surface of the sun. This is perfectly consistent with the first law of thermodynamics (conservation of energy), but would immediately violate the second law of thermodynamics, since you could in principle run a heat engine using the focal spot as the "hot" side of the engine, and the surface of the sun as the "cold" (!) side, thereby producing work using only one heat bath (the sun) rather than the conventional two.
To say the same thing in more detail: Let’s take a thermally non-conducting object and place it at the focal point of our system (point E in figure 1). A certain amount of energy falls on the image of the sun. The spot will heat up. Eventually it will become hot enough to glow. The temperature will stabilize at some temperature T such that the re-radiated power just matches the incident power. This temperature cannot be hotter than the surface of the sun; otherwise energy would be flowing from a (relatively!) cooler object to a hotter object, in violation of one of the corollaries of the second law of thermodynamics.
Funny story: When I was in junior high school, I was interested in amateur telescope making. I specifically wanted to build the ultimate rich-field telescope, one that gathered so much light that it would be possible to see beautiful nebulae and other deep-sky objects by looking through the telescope with my eyes (without photomultipliers and without making long time-exposures).
I tried really hard to design such a system. I went through reams of paper. If I made the aperture bigger at constant focal length, the exit pupil became too big (bigger than 7mm, the diameter of the dark-adapted eye). If I made the exit pupil smaller, it always seemed to come at the cost of more magnification than I wanted, meaning the image was too spread out, i.e. too few photons per unit area per unit time, i.e. too dim.
Eventually I gave up; I figured I just wasn’t smart enough to design the desired system.
Years later I learned about Liouville’s theorem, and realized that no such system is possible. Each of the deep-sky objects I was interested in is intrinsically so dim that even if you traveled there and stood next to the object, you couldn’t see it with the naked eye. (The beautiful pictures you see come from long time exposures, which the eye cannot do.) No system of lenses (or any other passive system) can produce an image with more surface brightness than the original object.
We have not proved Liouville’s theorem here; we have merely stated it and applied it to some interesting examples.
Liouville’s theorem can be taught at many levels. At the simplest level, it readily lends itself to discussion in terms of examples and pictures, such as in figure 1.
Phase space has a place of honor in the physicist’s toolbox. You don’t need it every day, but when you need it, you reeeeally need it.