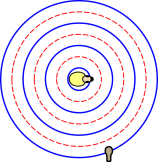
Figure 1: Duck Making Waves
Figure 1 is a snapshot of a duck sitting in the middle of a very large pond. The duck bobs up in down in such a way as to create ripples that radiate outward. A solid blue line represents the crest of a wave, while a dashed red line represents the bottom of a trough.
Near the bottom edge of the picture there is a cork floating in the water. The cork will move up and down in response to the waves. We can use the motion of the cork to turn the crank on an electrical generator, use the generator to light up a light bulb, and measure the amount of power. Let’s say that in the situation shown, exactly one unit of power is generated. We also choose to call this “one unit” of wave amplitude.
Figure 2 is the same as before, except now we have two ducks. The motion of the water at any point can be determined by adding the contributions of the two ducks. This is called superposition of waves.
These particular ducks bob out of phase, so that one duck is always going up while the other is going down. At the location of the cork, the combined effect of the two ducks is such that the surface of the water does not move up and down. Either duck separately would cause the cork to move, but the two ducks together do not. The crest of the wave from duck #1 exactly fills in the trough of the wave from duck #2.
We can quantify what we just said, as follows: The vertical displacement of the water at the position of the cork (at the time of the snapshot) can be described by the equation
| 1 + −1 = 0 (displacement) (1) |
That is, the displacement of the water due to the first duck is 1 unit upward. The displacement of the water due to the second duck is downward, which we represent as -1 units of upward displacement. The sum of these two contributions is zero. This phenomenon is an example of what we call interference between the waves, and in particular destructive interference since the motion due to one duck is destroyed by the presence of the second duck.
The displacement is zero not only at the time of the snapshot, but at all other times also. (This should be easy to see, by symmetry.) As a consequence, zero power is produced by the generator attached to the cork.
Now let’s see what happens with the power. The general rule is that power scales like the square of the wave amplitude. When we have either duck alone, the generator produces one unit of power. When we have both ducks working together, the generator produces zero power.
| (2) |
If we focus attention on power (rather than displacement), the last line of equation 2 makes a truly remarkable statement:
| (3) |
It is tempting to re-express equation 3 as 1+1=0, but that is not recommended. The “+” operator belongs to arithmetic, and has a well-defined meaning that should not be tampered with. In contrast, we can define the “&” operator to mean whatever we want. The meaning of equation 3 is that one unit of power (from the first duck) when superposed with one unit of power (from the other duck) makes zero power.
In fact, there is a whole set of points where exactly zero power can be produced, as shown by the line AB in figure 3. (There are many additional points where approximately zero power can be produced.)
If we take into account the fact that the wave amplitude decays as a function of distance from the duck, we see that some points on the AB line will be described as 1&1 makes 0, while others will be described as 2&2 makes 0, or by 3&3 makes 0, et cetera. The fact remains that there is zero wave amplitude (and zero power) everywhere along the AB line.
Figure 4 is the same as before, except that we have moved the cork to a slightly different location.
The displacement of the water in this situation can be given (to a good approximation) as:
| 1 + 1 = 2 (displacement) (4) |
Things get really interesting when we consider the energy and power. The power generated from one duck alone is (to a good approximation) one unit. The power generated from both ducks together is (to a good approximation) four units.
Why four? That’s easy to see from the kinetic energy, as follows: In a given amount of time, the water has to move twice as far (in accordance with equation 4). That means the velocity is twice as large, and the kinetic energy is therefore four times as large. Similar arguments apply to the potential energy: Just as Hooke’s law involves displacement squared, the potential energy of a water wave involves displacement squared. The force is twice as large, and the water has to move twice as far against this force. This is summarized by equation 5:
| (5) |
Let’s be clear: To a good approximation, with two ducks, our system with the cork and generator and light bulb can produce four times as much energy as with either duck separately. This is twice as much as you would predict by simply adding the power levels. The bottom line of equation 5 can be summarized as:
| 1 & 1 makes 4 (power) in phase (6) |
When the cork is in a slightly asymmetric position, the displacement contributed by one duck will be slightly greater than 1, while the displacement contributed by the other duck will be slightly less than one. This makes the math more complicated, since we can no longer summarize the result as 1&1 makes 2 on average. However, if you do the math properly, the main conclusion is unchanged: The classical result is not true in general, but is true on average if you average over the various true, wave-mechanical results.
In fact, there is a whole set of points where “extra” power can be produced, as shown by the line CD in figure 5. By “extra” we mean considerably more power than the sum of what could be produced from each duck separately.
You may be wondering what is the relationship between figure 3 and figure 5. Similarly you may be wondering what is the relationship between equation 3 and equation 6.
The answer has to do with phase. In situations where the waves from the two ducks arrive out of phase, we get destructive interference. In situations where the waves arrive in phase, we get constructive interference.
There are many different phases we can talk about. For starters, there is the phase relationship between the two ducks themselves. In the figures, the two ducks are 180 degrees out of phase – i.e. one duck is always moving upward when the other is moving downward – but other phase relationships are possible.
The power is most directly affected by another phase, namely the phase of the waves as they arrive at the location of the cork. This depends not only on the phase of the ducks that originate the waves, but also on how far away the cork is, relative to each duck.
In real life, ducks aren’t smart enough to maintain any definite phase relationship for very long, and they also tend to move around. That means we should consider taking the average over all possible phases. The various possibilities are summarized in the following equation:
| (7) | |||||||||||||||||||||||||||||||||||||||||
That is: As previously discussed, there are cases where 1&1 makes 4 and other cases where 1&1 makes 0. There are also cases where the two contributions are neither exactly in phase nor exactly out of phase, where it turns out that 1&1 makes 2 or thereabouts.
The remarkable thing is that if we average over all possible phases, we find 1&1 makes 2 on average.
Let’s be clear: The classical rule that 1&1 makes 2 is not the general rule. We have just explained why the classical rule is valid in situations where it is appropriate to average over all possible phases. (Another way for it to be valid is discussed in section 2.)
If you didn’t know about anything except the classical result, you might think the physical statement that 1&1 makes 2 is “explained” by the mathematical statement that 1+1=2 ... but we have seen that this cannot be a valid explanation. Remember that 1+1=2 always, whereas 1&1 makes 2 only in the classical limit.
This analysis is not restricted to ducks on ponds. It applies to all waves ... and it turns out that lots of things can be analyzed using wave mechanics (in combination with other techniques).
Suppose we have a vector V1 that points north, and a second vector V2 that also happens to point north. Both vectors have unit length. If we add the two vectors together, the sum (V1 + V2) has length 2. For present purposes, for any vector V, we shall be less interested in its length than in its absolute square, denoted |V|2. (For vectors over the real numbers this is just the dot product of the vector with itself. For vectors over the complex numbers, this is the contraction of the vector with its conjugate transpose, and you should beware that V2 ≠ |V|2.)
Now let’s see what happens if the second vector is not necessarily in the same direction as the first vector. (Both vectors still have unit length.) Here is a sampling of the possibilities:
| (8) |
We see that if we average the absolute square over all possible directions, it averages out to 2. This is the sum of the absolute square of V1 plus the absolute square of V2.
We can understand this algebraically and geometrically with the aid of the following equation:
| (9) |
If we average over all possible directions, the cross terms vanish by symmetry.
What’s more, in a high-dimensional vector space, the cross terms almost always vanish even if we don’t average over all directions. This happens because in a high-dimensional space, it is very likely that two vectors chosen at random will be mutually perpendicular, or nearly so, and for perpendicular vectors we have the Pythagorean result depicted in figure 6, where the squared length of the resultant is equal to the sum of the squared lengths of the contributions. You can begin to see this in equation 8, where most of the rows involve perpendicular vectors, and these rows already uphold the simple rule (addition of absolute squares) even before we average over phases.
As an important example, there are situations where
| (10) |
The rule that 1&1 makes 2 applies to electrons only in the classical limit. There are some situations where electrons do exhibit classical behavior, but there are also many common situations where they do not. Nonclassical situations include the electrons inside atoms, and the conduction electrons electrons in an ordinary metal.
You can be pretty confident that the rule 1&1 makes 2 applies to ping-pong balls under ordinary conditions, for two reasons:
For one thing, the quantum-mechanical wavelength of a ping-pong ball, at ordinary temperatures, is vastly smaller than the ping-pong ball itself. So the averaging required to produce the classical limit happens on a very small length-scale (and a very small time-scale).
Secondly, with high probability, two ping-pong balls will not be exactly identical. We assume that one of them contains a few more atoms than the other. Such objects are represented in the equations of motion by vectors in a high-dimensional space, and the vectors are perpendicular if the objects contain different numbers of elementary particles. Therefore the ping-pong balls behave classically even at arbitrarily low temperatures, whether or not average over phases, for reasons explained in section 2.
An interesting intermediate case involves things the size of entire atoms, helium atoms for example. Let’s assume we have a sample of isotopically-pure 4He liquid. All 4He atoms are identical, so we don’t need to worry about the issues raised in section 2; the wavefunction is a single complex number, not a vector. At room temperature, the helium atoms are classical – just as classical as ping-pong balls. But if you cool liquid helium within a couple degrees of absolute zero, the quantum-mechanical wavelength becomes long enough that interference effects become significant – overwhelmingly significant. The liquid helium becomes a superfluid.
A simple but spectacular example of constructive interference is a laser. A laser works by adding together a number of low-power waves ... but because the phases are just right, the output power is vastly greater than what you would get just by adding the low-power waves with random phases.
Another spectacular example concerns the proverbial mutability of clouds. Have you ever wondered how a cloud can form, then change shape, and then vanish into the clear blue sky? We know that clouds are made of water molecules ... but the total water content of a parcel of sky is the same before and after the cloud vanished. The difference is that a cloud consists of droplets of water. In each droplet there are millions of water molecules, all sufficiently close together that they can contribute in phase to scattering a light wave. In contrast, after the droplet evaporates, the water molecules spread out over sufficiently large distances that their contributions combine with all possible random phases. Therefore in the blue sky there is some scattering, but millions of time less than in a cloud.
What could be more definite than 1&1 makes 2? What could be more well-known? It is proverbial that 1&1 makes 2. Indeed it is beyond proverbial; it is a cliché.
However, we have just seen that 1&1 makes 2 is not the general rule. Instead, physics tells us that 1&1 makes 2 for distinguishable particles. Also 1&1 makes 2 on average, even for indistinguishable particles.
Meanwhile, the arithmetical rule 1+1=2 remains true, always. It represents the classical case.
This illustrates the difference between mathematics and physics. In simple cases, the physics is well represented by simple mathematics. In other cases, we need considerably more complicated mathematics in order to represent the physics.
Conversely, sometimes physics is used to model the mathematics. For example, suppose we use physics and engineering to build a computer to help us do arithmetic and/or image processing. We must be careful to eliminate unwanted wave-mechanical interference phenomena (by averaging over all possible phases, if necessary), because otherwise the computer may fail to get the desired (classical) answer.
The expression 1+1=2 is a linear equation. Lots of things in physics – and in life in general – are nonlinear.
The alert reader may have noticed that the conclusions of section 1 (waves) and section 2 (vectors) are rather similar. This is not a coincidence. Water waves can be well represented by a complex number, which in turn can be represented by a two-component vector. This is called the phasor representation. This two-component vector exists in an abstract space; it does not point north/south, east/west, or up/down.
Although some people treat the terms “identical” and “indistinguishable”as synonymous, there are many who make the following rather subtle distinction. All of the following statements are true:
For a spin-up electron and a spin-down electron, most of their quantum numbers are the same; for example the charge is the same and the total spin (s·s) is the same. The question arises, how many quantum numbers can be different before we judge two particles to be non-identical (not just distinguishable). I suspect there is no clear answer to this question. Fortunately, we do not need a clear answer. We don’t need a precise definition of identically, because it doesn’t matter. The laws of physics depend on indistinguishability, which requires all of the discrete quantum numbers to be the same.