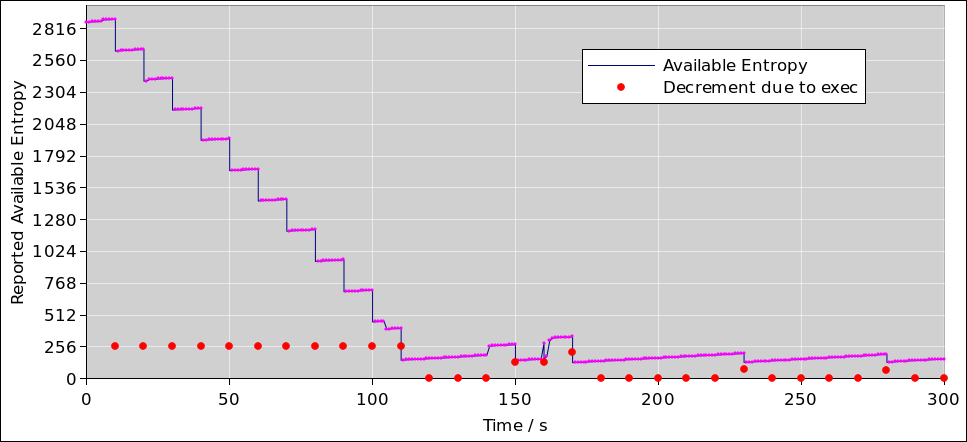
Figure 1: Reported Available Entropy versus Time
Copyright © 2013 jsd
Here are some specific observations and questions about the code in drivers/char/random.c. Line numbers refer to release 3.11.
However, this leaves us with a basic question about architecture and strategy, because the device is operated in such a way that the buffers are almost always empty or nearly so. Observations indicate that the input pool is almost always at or below 192 bits, and the other pools are almost always at zero.
That is not enough entropy for expected uses such as cutting PGP keys. This seems to conflict with the stated purpose of /dev/random, and the purpose of having buffers within the device.
In contrast, the output pool associated with /dev/random does not need to perform any of those functions. It therefore seems odd that it has the same complex structure as the input pool. It needs no mixing and no hashing, because (unlike the input pool) it is being fed from a source of concentrated, high-grade randomness, i.e. an entropy density of 8 bits per byte. It seems one could get rid of this pool entirely, thereby improving memory usage and computational efficiency, with no harm to security, indeed no downside at all.
Rationale: It is desirable to have a reasonably large amount of entropy stored in the driver’s “input pool”. That’s because the demand for high-grade randomness (via /dev/random) is very bursty. When cutting a key, there is commonly a sudden demand for several hundred bits, if not more. Therefore, in the common situation where there is a steady moderate load on /dev/urandom and a bursty load on /dev/random, the current code has a serious performance problem, due to not enough stored entropy. Increasing the reserved entropy would greatly improve the usefulness of /dev/random and would have no impact on /dev/urandom.
To say the same thing the other way, right now there is no maximum on the amount of entropy that /dev/urandom can take from the “input pool” whenever the pool entropy is more than twice the wakeup threshold. There should be a much lower limit. Making the entropy density of /dev/urandom any higher than it needs to be just wastes entropy. It does not materially increase the security of /dev/urandom, and it harms /dev/random.
I have code that deals with this, using an adaptive, cooperative resource-sharing approach. The result is that the input pool is almost always full, rather than almost always nearly empty.
It would seem there needs to be some sort of load-balancing, so that /dev/urandom gets enough entropy to reseed itself sufficiently often. See reference 1 for why this is important.
Fixing this is not a trivial exercise, but I have some code that seems to be a significant improvement.
There is no documentation as to the semantics of "nbytes". Furthermore, the variable name exhibits a classic poor programming practice. It tells us that "n" is measured in "bytes", but it tells us nothing about the semantics of "n". It is important to keep track of the units of measurement, as the Mars Climate Orbiter mission discovered – but that is not the whole story. By way of analogy, kinetic energy, potential energy, lagrangians, torque, and lots of other things can all be measured in the same units, but the semantics is very different.
My best guess is that the code needs to do a subtraction to calculate the amount to be added. If this is not right, somebody should please explain what is going on.
On the other hand, sometimes reading from /dev/random can drain the entropy_avail all the way to zero.
I do not understand what I am seeing here.
Typically /dev/urandom consumes either too much entropy or not enough entropy. Observations indicate that in the typical case, there is a moderately high demand on /dev/urandom. Then, if the available entropy is above the reserve, /dev/urandom gobbles up essentially all new incoming entropy (not all at once, but sooner or later, in batches). This is too much. On the other hand, if the available entropy is below the reserve, /dev/random uses none of the entropy, which is too little.
In other words, the normal load on /dev/urandom is tantamount to a denial-of-service attack on /dev/random, because the reserved available entropy – 128 bits – is not enough for ordinary applications, which tend to place a brief but sudden high demand on /dev/random, demanding several hundred bits all at once.
Conversely, a rather modest load on /dev/random is tantamount to a denial-of-service attack on /dev/urandom, insofar as it means that /dev/urandom will never get reseeded, i.e. will never recover from compromise.
The existing version is partly yarrow-like and partly not. It is yarrow-like in the sense that it performs updates in batches, with a substantial minimum batch-size. It is non-yarrow-like in that it presents far too much load on the upstream source of entropy.
I have some code that makes it possible to do resource-sharing.
Reference 2 asserts that /dev/random is “not robust” but their definition of “robust” has not met with universal acceptance.
I disagree with the assertion that it is «perhaps impossible» to to obtain a proper estimate of the entropy-content of a source. A constructive counterexample is provided in reference 3.
Figure 1 records some observations of the behavior of /dev/random.
Here are the conditions of the experiment:
2>/dev/null ls -al /proc/*/fd/* | egrep '/u?random'
I don’t understand the details, but all evidence suggests that the exec consumes 256 bits from /dev/urandom. You can see this clearly in the figure, in the section from time t=0 to t=180 seconds. Every time there is an exec, the reported entropy drops. The amount of drop is shown by the red dots in figure 1. The entropy is measured immediately before and immediately after each exec, so it is hard to imagine that there is any other explanation for the drop.
The initial condition – i.e. a relatively high entropy at t=0 – would be highly unusual for a system not running turbid.
In contrast, the section from time t=180 seconds onward should be considered the normal situation for a system not running turbid. There is something in the kernel – I don’t know what – that is contributing entropy to the /dev/random pool at the rate of approximately 1.2 bits per second. You can see this in the slight upward slope of the graph. Meanwhile, the long-term average entropy-output via /dev/urandom exceeds the long-term intropy-input. The result is that the available entropy in the pool is (a) very small and (b) exhibits a sawtooth pattern. As soon as the pool entropy gets above 192 bits, the next time there is any load the entropy drops by 64 bits, dropping down to slightly more than 128 bits. In more detail, if you read the code in drivers/char/random.c, you discover that the magnitude of the drop, i.e. the height of the tooth, is equal to the “read_wakeup_threshold” which is normally 64 bits but can be changed at runtime via /proc/sys/kernel/random/read_wakeup_threshold. The lower bound of the sawtooth is twice this number.
The device would be in some ways better and in no ways worse if the lower bound were higher, several thousand bits higher.
We should also consider a situation not shown in the diagram, namely a situation where there is a small long-term demand on /dev/random. This could easily exceed the long-term entropy-input. This would cause the process reading /dev/random to be rate-limited, which is undesirable but not fatal. What’s worse is that in this situation exactly zero bits of entropy would be used for /dev/urandom. The PRNG will never get rekeyed.
Copyright © 2013 jsd