The second example is that of a source (or sink), the complex potential of which is

This is a pure radial flow, in which all the streamlines converge at the origin, where there is a singularity due to the fact that continuity can not be satisfied: at the origin there is an input (source, m > 0) or output (sink, m < 0) of fluid. Traversing any closed line that does not include the origin, the mass flux (and then the discharge) is always zero. On the contrary, following any closed line that includes the origin the discharge is always nonzero and equal to m.

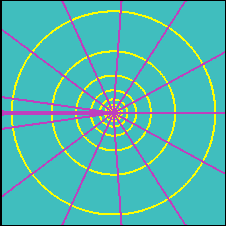
The thick magenta line on the left is related to the fact that the complex potential is, in this case, a multi-valued function of space. At any fixed point, the potential is known up to a constant, the so-called cyclic constant, that in this case has the value of . Since, in general, the potential is defined up to a constant, the fact that it is a multi-valued function of space does not create any problem in the determination of the flow field, which is uniquely determined upon deriving the complex potential W with respect to z.