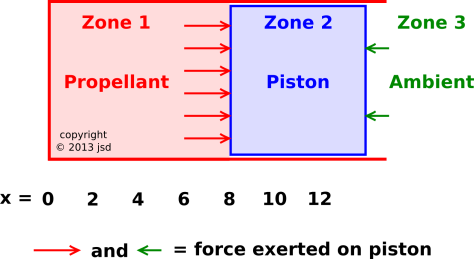
Figure 1: Air Gun
:
Let’s consider an air gun, as shown in figure 1. This is borrowed from reference 1. Zone 1 contains some pressurized gas (the propellant). Zone 2 is the piston. Zone 3 is the ambient atmosphere.
The system starts out at rest, with the piston at x=1. (We measure the position of the piston by the location of its left edge, since that is what determines the volume available to the propellant.) Initially the propellant is at a high pressure, many times the ambient pressure. Then at t=0 we release the piston. The propellant expands. The diagrams in this section are a snapshot of the situation at some later time, during the expansion.
The forces exerted ON the piston are indicated by the arrows in figure 1.
Meanwhile, we can also ask about the forces exerted BY the piston; these are indicated by the arrows in figure 2.
By comparing figure 1 with figure 2 we can verify that the third law of motion is upheld: For every force exerted on A by B there is an equal-and-opposite force exerted on B by A.
The smart way to proceed is to reformulate things in terms of momentum flow. This works for a huge range of tasks, from the very simple to the very complex. There is a perfectly well defined boundary at x=8, and we can unambiguously talk about the momentum flowing across this boundary. This is shown in figure 3. As in reference 1, we represent momentum flow by a double arrow: The black half of the arrow indicates the direction of flow (namely rightward), while the colored half indicates what is flowing (namely rightward momentum).
In figure 3 you can see that rightward momentum is flowing into the piston faster than it is flowing out. That means that over time, momentum will accumulate in the piston.
If we wanted to analyze the air gun semi-quantitatively, we could start by making some simplifying assumptions:
- 1) We want to talk about “the” pressure of the propellant gas. We assume this is a well-defined quantity. In particular, we assume that at any given time, the pressure is spatially uniform throughout Zone 1. This requires (among other things) that the velocity and acceleration of the piston be not too large, on a timescale set by the speed of sound and other factors.
- 2) Similarly we assume “the” pressure of the ambient atmosphere is well defined. We assume it is not only uniform in space but constant in time. Again this implies no sound waves.
Those assumptions are not valid for real firearms, but are perhaps acceptable simplifying assumptions for a toy air gun. So far so good.
Once upon a time I ran across a version of this problem with an additional assumption:
- 3) Assume that the mass of the piston is very small. This is to ensure that the piston contributes nothing to the pressure, force, momentum, or energy of the situation. ☠
Now we have a problem. Assumption (3) is inconsistent with the other two assumptions, or inconsistent with the laws of physics; take your pick. That’s because in any situation where there is an unbalanced force on the piston, energy must be transferred to the piston as it moves. Putting a significant amount of energy into something with a very small mass means that the velocity must be very large, which contradicts assumptions (1) and (2).
In more detail: The thermodynamic equation of state tells us the pressure as a function of volume. We can then integrate PdV (or equivalently Fdx) to find the work done on the piston by the propellant. Similarly we can calculate the work done on the piston by the ambient atmosphere, which will be smaller and negative.
Once we know the net work done on the piston, we know the kinetic energy of the piston. We know this absolutely, via the work/kinetic-energy theorem, as discussed in reference 2. This is an actual theorem, and there is no way around it. This energy is independent of the mass of the piston. You cannot make this energy go away by reducing the mass of the piston.
Some people may want to have a nice simple system where the piston is negligible, but as the famous philosopher Jagger once said, you can’t always get what you want. If you reduce the mass of the piston, or remove it entirely, you guarantee the system will not be simple. There will be a sudden, high-velocity expansion with lots of sound waves and other hard-to-analyze phenomena.
Let E represent the energy of some system. For example, E1 represents the energy contained in Zone 1 in our air gun.
Subject to the usual mild restrictions, we can write the exterior derivative of of E as
| (1) |
In some sense we can take equation 1 as the definition of T and P.
Next, we introduce the enthalpy H:
| (2) |
Using the sum rule and product rule from basic calculus, we can write the exterior derivative of H as
| (3) |
There are a lot of useful things you can do with the enthalply. For example, if you choose to do an experiment under conditions of constant pressure, then the VdP term is automatically zero, which simplifies the calculations.
All the variables we have been using are functions of state. For example, H1 is a function of the thermodynamic state of Zone 1. Specifically, we can rewrite the general expression in equation 2 in more concrete terms, applying it specifically to Zone 1:
| (4) |
In contrast, it would make no sense to write the enthalpy of Zone 1 in terms of the ambient pressure P3, as in
| (5) |
or anything like that.
If this seems obvious to you, that’s good. On the other hand, beware that there are widespread misconceptions about this. Let’s try to understand why.
It turns out that 99.9% of the experiments that get done in the introductory chemistry lab are done in open beakers, which means that the pressure on “the system” is equal to the ambient atmospheric pressure. Lots of p-chem books base their discussions on the assumption of open-beaker conditions. That’s acceptable as a pedagogical starting point, but it is not a satisfactory ending point.
By assuming open-beaker conditions, they can more-or-less get away with using P3 in place of P1. The resulting ideas and formulas are conceptually wrong, but they give numerically correct answers, provided you apply them only to situations where P1 is numerically equal to P3.
In contrast, if you apply an equation such as equation 5 to a situation where P1 is not numerically equal to P3, you get totally wrong answers. To say the same thing another way, the principled approach in equation 4 always works. The dirty approach in equation 5 works in some situations, depending on assumptions and/or coincidences, but it does not generalize to other situations.
Another tremendous problem is that introductory books often frame the discussion in terms of “the” system and “the” ambient environment, as if those were the only two things in the universe. Again, that may be OK as a pedagogical starting point, but it is not a satisfactory ending point.
The system-versus-environment way of thinking is a disaster when applied to our air gun. There are at least three zones that must be considered. If you try to make Zone 2 negligible by reducing the mass of the piston, you make the analysis more complicated, not less, because then you need to divide Zone 1 and Zone 3 into thousands of sub-zones, in order to account for the local variations in pressure and temperature that result from the sudden violent expansion.
Here is a third misconception, which can be seen as a combination of the previous two: If you adopt the oversimplified system-versus-environment way of thinking, or otherwise assume that the propellant is in direct contact with the ambient environment, then you would conclude that P1 must be equal to P3. It would, hypothetically, be required by the third law of motion.
However, the reality is far different, as we see if we do a proper three-zone analysis. The third law of motion requires that the force exerted by the propellant on the piston (at x=8) be equal-and-opposite to the force exerted by the piston on the propellent (at the same place, x=8). You can see this by looking at the force vectors, comparing figure 1 to figure 2.
Meanwhile, it should be clear from the diagrams that the pressure on the propellant (Zone 1) is not even remotely the same as the ambient pressure (Zone 3). Zone 1 is not in contact with Zone 3. The two pressures have got nothing to do with each other during the expansion. (They may become equal long after the expansion is over, but that is not the subject of our discussion.)
Given that the initial pressure in Zone 1 is large, during the expansion the lion’s share of the energy goes into the piston. It does not go into the ambient atmosphere.
Again we conclude that the piston is not negligible and cannot be made negligible, not by reducing its mass or otherwise ... unless you violate assumptions (1) and (2), thereby making the system very much more complicated.