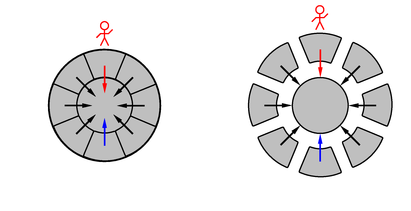
Figure 1: Nonuniformities in the Earth’s Gravitational Field
A uniform gravitational field is indistinguishable from an acceleration of the reference frame. (This is called the equivalence principle, also known as Einstein’s principle of equivalence.)
Similarly, the following statements are valid locally, to first order: Any gravitational field is locally indistinguishable from an acceleration of the reference frame. That means, to first order, that if you are in a freely-falling elevator, you (and the objects around you) will be weightless in the frame of the elevator. You have no way of knowing the direction or magnitude of the gravitational field, since you and your frame of reference are moving together. This is called the Einstein elevator argument, although Galileo made the same argument in 1638.
On the other side of the same coin, if the gravitational field is nonuniform, there is no choice of reference frame that will make the nonuniformities go away. Actually there are three considerations:
If the field is sufficiently uniform, it looks uniform. If the measurements are sufficiently local, the field looks uniform. If the measurements are sufficiently insensitive, the field looks uniform.
Einstein’s principle of equivalence is simple, elegant, and powerful … but it is also very limited, because it applies only to small regions and/or to uniform fields.
Locally you cannot feel a gravitational field. In ordinary life, as you walk across the earth, you don’t feel gravity. What you feel is the mechanical stresses that are exerted by the earth against your feet, and then transmitted throughout your body.
To say the same thing another way, falling off the 4th floor balcony doesn’t hurt a bit. What hurts is the sudden stop when you hit the ground.
To say the same thing a third way, consider standing in a rocket ship that is hovering a little ways above the earth’s surface (not orbiting, just hovering, stationary). [This scenario was suggested by Jeffrey Schnick.] Initially the rocket is supplying 1G of upward acceleration, just enough to cancel the conventional gravitational field. If now the gravitational field is switched off, observers inside the ship will not feel any change. They will not notice anything, unless they look out the window. What they continue to feel is the 1G acceleration of the rocket, which is now no longer stationary, but is accelerating upward from its original position. In contrast, if you leave the gravitational field on, but switch off the rocket engines, the observers inside the ship will immediately feel the change. They will experience the feeling of being in free fall. This is sometimes called the feeling of weightlessness, but remember that they are only weightless in the frame of the rocket ship, whereas they still have weight in the terrestrial lab frame. This is yet another way of illustrating that gravity – in the form of a uniform gravitational field – is not what you feel. What you feel is the fact that your surroundings are (or are not) freely falling.
Of course, nonuniformities in the field are directly observable. Tidal stresses on earth are far, far to small for the human body to perceive directly. On the other hand, we can observe how tidal stresses interact with the oceans to produce the observed tides, as discussed in reference 1. Another example can be seen in figure 1, as we now discuss.
Imagine that an observer is standing on top of the earth, as shown on the left side of the figure. The right side of the figure is the same, except that we imagine the earth has been divided into a number of separate chunks. In the limit of a large number of small chunks, the gravitational field is more-or-less uniform in the vicinity of the observer. The observer and the chunk he is standing on accelerate toward the center of the earth at the same rate as indicated by the red arrow. That means the observer is weightless with respect to the frame attached to the chunk he is standing on (to first order in chunk-size).
The only reason the observer and his chunk do not fall freely and weightlessly forever is that the other parts of the earth are in the way. They fall at different rates and/or in different directions. In equilibrium, as shown on the left side of the figure, you can imagine that all the black arrows cancel by symmetry, while the red arrow is balanced by the blue arrow on the far side of the earth. (This is not the only way to do the arithmetic, but it is not wrong.) In any case, all the non-red arrows collectively apply mechanical forces to the earth that balance the force of the red arrow. This arrests the otherwise-free motion of the observer and his chunk. There is nothing “pseudo” about these forces; they are real mechanical forces within the earth. The resultant of these non-red forces is exerted upon the observer’s chunk and thence upon the observer, and this is what creates the observer’s conventional perception of his weight.
Let’s be clear: On the right side of the diagram, the blue chunk is undergoing uniform acceleration, while the red chunk and the observer are undergoing uniform acceleration in the opposite direction. It is only when we make a non-local comparison between these two accelerations that observable forces arise. These are mechanical forces, transmitted through the earth, as shown on the left side of the diagram.
To return to the question of whether gravity can be felt, it is rather like Archimedes and his lever: If you give me a place to stand, and a robust connection to places on the far side of the earth, I can feel the nonuniformities in the gravitational field by making a very nonlocal comparison, comparing the field “here” to the field “there”.
Also keep in mind the dependence on instrumental sensitivity. There exist devices called gravity gradiometers that measure nonuniformities in the gravitational field. These are exquisitely sensitive and delicate instruments. Such an instrument compares the field “here” with the field a few centimeters away, so it is a nonlocal measurement in the technical sense, but only slightly nonlocal. One might call it quasi-local.
It is worth emphasizing that all notions of weight (and weightlessness) are frame dependent.
As discussed in reference 2, a pencil is weightless in the frame of the space station because of the motion of the frame, not because of the motion of the pencil.
This is true, important, and often hard for students to grok. I use this as something of a litmus test: they understand weightlessness if-and-only-if they understand the frame dependence.
There are some situations where you might want to evaluate the weight of an object using a frame attached to the object, as John Mallinckrodt has pointed out ... but this is a special case, not the general case. It is usually much simpler to keep the frame separate from the object. Even you find a frame that is instantaneously comoving with the object, it is still conceptually separate.
I can be weightless whenever I want, simply by thinking of a local freely-falling reference frame. In that frame, I am held in my chair by the fact that the chair is accelerating skyward at the rate of 9.8 m/s/s. In this sense, there is no special feeling associated with weightlessness.
The special feeling associated with riding in the Vomit Comet comes from the fact that you can be in free fall for 25 seconds at a time. Similarly, in the space station you can be in free fall for weeks at a time. I emphasize that you can be in free fall while having weight (in the terrestrial lab frame) and/or in free fall without weight (in the frame of the vehicle). It feels the same in either case.
If you want to be technical about it, you never feel your weight, not in any frame. What you feel is the force of the floor, chair, etc. pushing against you. This push is not a in any direct sense a gravitational interaction; it has more to do with the KE and electrostatic PE of the atoms and molecules.
(You could in principle feel a tidal stress, but under ordinary conditions that is far, far to small to be noticed.)