|
|
| |
| Figure 1: One-Dimensional Number Line | Figure 2: Two-Dimensional Number Plane | |
| (e.g. Charge) | (e.g. Apples and Oranges) |
The most important things to know about electrical charge are:
The first ideas is related to all the others. For starters, in the charge-conservation law, only one type of charge appears. There is only one charge-related variable. If there were multiple kinds of charge, we would need a separate law for each one. The same goes for the Maxwell equations and the Lorentz force law.
Ordinary low-tech electrical measurements do not distinguish between one component and two or more. However:
It is crucial to distinguish the concept of particle from the concept of charge. Like other fundamental concepts, such as mass or energy, charge is abstract. A proton is a tangible particle, but charge is an abstraction. The idea of proton is not equivalent to the idea of positive charge, because there are lots of things that have positive charge but don’t contain protons, e.g. muons, pions, positrons, et cetera.
| Charge | Particles |
| Abstract. | Tangible. |
| There is only one kind of charge. You need only one variable to keep track of the charge. | There are lots of different charge-carrying particles. You need lots of variables if you want to keep track of the particles. However, that’s not charge. The number of particles is the answer to a different question. |
| Again: To keep track of charge itself, you need only one number. | To keep track of the charged particles, you can sometimes get away with using only two numbers, but only approximately. Really you should allow for many numbers, because there are many charge-carrying particles, as discussed in section 4. |
| The amount of charge might be positive or it might be negative, but it can’t be both at the same time. It’s only one number. | You can have some number of positively-charged particles and negatively-charged particles at the same time. |
| Charge is an abstraction, not to be confused with the details of any particular charge-carrying particles. | Knowing the amount of charge will not tell you which type(s) of charged particles are present, nor how many. |
| Charge is charge. There is only one kind of charge. | There are lots of things we could talk about (e.g. momentum) that are not charge, not particle-number, and not even closely related to either one. |
It is sometimes useful to distinguish the weak two-component model from the strong two-component model, as discussed in section 3.1.
The one-component model is recommended. The strong two-component model is not completely crazy, but it’s not a model of charge. It’s a model of something else. In particular, observations that are consistent with the two-component model are absolutely not evidence against the one-component model. The weak two-component model is consistent with the evidence, but the one-component model is equally consistent and should be preferred on the basis of simplicity and convenience.
It must be emphasized that for all practical purposes, the one-component model is the right way to think about electrical charge.
However, to be scientific, we must consider all the plausible hypotheses. If we do that, we find there are actually multiple versions of the multi-component model, namely the weak version and the strong version.
This model is not provably wrong ... but I don’t recommend it. It is more complicated than the one-component model, but makes essentially the same predictions.
This model is provably wrong. Protons are not conserved. Electrons are not conserved. For example, a neutron can decay into a proton plus an electron. Electrical charge is conserved, but the various kinds of particles are not conserved.
You could imagine a model with more than two components, where each type of particle is its own component. However, these components must not be called kinds of charge. They are kinds of particles. Charge is something else. See section 4.1.
| The fact is, as far as anybody can tell, there is only one kind of charge. We only need one variable to describe charge. If you have a theory that requires two variables, it’s not necessarily crazy, but it’s not a model of charge; it’s a model of something else. |
However, in a great many textbooks and encyclopedias, one can
find statements alleging that:«There are two kinds of charge, namely positive charge and negative charge.» ☠
|
| This expresses what is called the one-component model of electric charge, which is the recommended model. | This expresses the two-component model. We will have nothing good to say about it. |
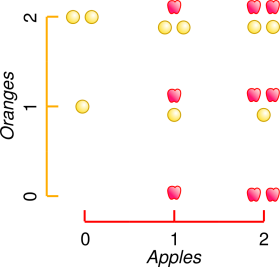
| In reality, the charge can be represented as a point along a one-dimensional number line, as shown in figure 1. More positive charge is represented by points farther to the right on the number line, while more negative charge is represented by points farther to the left. | If we really did have two kinds of things – like apples and oranges – we would need two variables to describe the situation. The amount of the two different kinds of thing would be represented by a point on a two-dimensional coordinate plane, as in figure 2. |
| Positive charge cancels negative charge and vice versa. | Apples do not cancel oranges nor vice versa. Electrons do not cancel protons, or vice versa. If you add electrons to protons in the ordinary way (excluding nuclear reactions) the electrons are still there and the protons are still there. |
|
|

| |
| Figure 1: One-Dimensional Number Line | Figure 2: Two-Dimensional Number Plane | |
| (e.g. Charge) | (e.g. Apples and Oranges) |
| The charge of the electron is different from the charge of the positron, but this is a difference in amount, not a difference in kind. The electron-charge is represented by a point on the number line, while the positron-charge is represented by another point on the same number line. |
| The key point is that only need one variable to describe the charge of any given object. At any given time, this variable may be positive, negative, or zero, but it is still just one variable. | If there were two kinds of charge, we would need two variables to keep track of them. |
| |
Note: Some people use the word fluid, so they speak of a one-fluid model (as opposed to a two-fluid model). That’s essentially just another name for what we are calling the one-component model (as opposed to the two-component model). We prefer the latter name because charge isn’t exactly a fluid. It is an abstract quantity. It does, however, exhibit conservation and continuity in close analogy to the flow of a compressible but indestructible fluid. Conservation of charge implies continuity of current. For more on what we mean by conservation and continuity, see section 6 and reference 1.
If you think of charge as a fluid, please do not imagine that it behaves like an «incompressible» fluid. In fact there are many situations where the density changes dramatically as the charge flows along. A video of this, and additional discussion, can be found in reference 1.
Also note the following contrast:
| In the real world, some quantities can be positive, negative, or zero. Consider for example elevation relative to sea level. For example, the elevation of Furnace Springs, California, is a negative number. | To be sure, there are some quantitites that can never be negative, such as the number of apples in a basket. However, that does not change the fact that there are plenty of other quantities that can be positive, negative, or zero. |
Some textbooks use the two-fluid language only in passing, using it as nothing more than a figure of speech, which isn’t so bad. However, others go out of their way to argue that the two-fluid model is right and therefore the one-fluid model must be wrong, which is appallingly illogical.
In situations where the charge is what matters, you don’t need to keep track of each kind of particle separately. It suffices to keep track of only one thing, namely the charge. This is a valuable simplification.
In other situations, you might prefer to keep track of the various kinds of particles for some reason, or for no reason at all. This is more complicated, but it is perfectly OK. Beware that there are a great many kinds of charged particle, not just two.
Positrons have been known since before muons, but positrons are relatively inconvenient to obtain in a high school setting.
Bottom line: If we look only at the evidence that was available in Ben Franklin’s day, the two-component model and the one-component model are equally consistent with the data. It would be grossly fallacious to take an observation that is consistent with the two-component model and use it as evidence against the one-component model. Using only ancient evidence, the one-component model should be preferred on the basis of simplicity and convenience.
The weak two-fluid model is not provably wrong, but it has no advantages over the one-fluid model, and is unnecessarily complicated.
On the basis of more modern evidence we know that the strong two-fluid model is not a model of charge; it’s a model of something else.
Within the field of atomic physics, there is a sub-field where we deal with three kinds of elementary particles: protons, neutrons, and electrons. These things are different in kind. To keep track of them, we need three numbers.
Interestingly, the three numbers that are conventionally used are not the simple particle-counts, but rather the following:
To fully specify an atom or atomic ion, it suffices to specify the three numbers (A, Z, q). For example:
If I tell you only that A=7 and Z=3, you have no idea what the charge is. You know it is lithium, but you have no idea whether it is ionized or not.
Conversely, if I tell you only that q=1, know the charge. The charge is 1 unit. You have no idea how many electrons, protons, or neutrons there are, but you know the charge. It could be Li+ or Na+ or Cu+ or lots of other things, but whatever it is, it bears one unit of charge.
To summarize: In this narrow sub-field, there are three kinds of elementary particles, but only one kind of charge. It takes three numbers to specify the particles, but it takes only one number to specify the charge.
More generally, there are dozens upon dozens of different kinds of particles, but still only one kind of electric charge. In physics, there are dozens of kinds of charged elementary particles but only one kind of electric charge; see figure 3. In chemistry, there are dozens upon dozens of charged atomic ions, not to mention molecular ions, but still only one kind of electric charge; see figure 5.
| In 1733, du Fay argued that there were two kinds of electricity, namely “vitreous” electricity and “resinous” electricity. |
| In 1747, William Watson argued in favor of a one-fluid model. Benjamin Franklin independently came to the same conclusion at the same time. Indeed, Franklin introduced the terms “positive”, “negative”, and “charge” for precisely this reason, to indicate a surplus or a deficit of the one type of electricity. See reference 4. | Ever since 1747, the weak two-fluid model has remained viable. It isn’t provably wrong. It is only marginally worse than the one-fluid model. In particular, we can restate the weak two-fluid model in modern terms: We classify the positive charge-carrying particles as «vitreous electricity» and classify the negative charge-carrying particles as «resinous electricty». This leaves us with a model that is impractical but not provably wrong. |
| The usual «proofs» of the two-fluid model are completely wrong, but that is not a sufficient reason to reject the model. |
| In 1865, the Maxwell equations were published. These equations give an extraordinarily good description of classical electromagnetism. This is relevant because the Maxwell equations imply that charge is conserved. So there is one kind of conserved charge. | This doesn’t settle the argument, because if you think that “vitreous” and “resinous” electricity are separately conserved, then as a corollary, the difference of the two (i.e. the net charge) is also conserved, as in equation 1a. Perhaps the Maxwell equations are merely a corollary of some deeper two-component theory. |
| In 1932, the positron was discovered, confirming a prediction made by Dirac in 1928. This invalidates the strong two-fluid model. The number of electrons is not conserved. Protons are not the only carriers of “vitreous” electricity. | This is the end of the two-component theory. Either you need more than two components (to keep track of the particles) or just one component (to keep track of the charge). |
| The newly discovered charged particles contribute to the charge in exactly the same way as the old ones. No changes to the Maxwell equations are required. | A multi-component model is not necessarily crazy, but it’s not a model of charge. It’s a model of something else. |
| An additional stake was driven through the heart of the two-fluid model in 1964, when the subnuclear color charge was figured out. It is now very clear what an interaction looks like when it has to be described using more than one variable. See section 7. Note that color charge is completely independent of the ordinary electric charge. There is still only one kind of electric charge. |
So, for more than 80 years, it has been known that there are more than two types of charged particles, and the particles themselves are not separately conserved. The only conserved thing that resembles electrical charge is the charge itself. There is only one such thing.
It is more important to know what charge does than to argue about what charge «is». Consider the following contrast:
One indispensable property of charge is its role in the law of conservation of charge. This is the starting point and the linchpin for any understanding of what we mean by charge. The law of conservation of charge states that the amount of charge in a given region cannot change except by flowing across the boundary of the region. This law can be stated with great precision and formality, and has been extensively checked and confirmed. It stands on its own as a fundamental law of nature ... and it can also be derived as a corollary of the Maxwell equations. For more on what we mean by conservation, see reference 1.
Suppose we start with a negatively-charged pion, which decays into a muon, which decays into an electron, as outlined in figure 3. There are also various neutrinos involved, as indicated by the gray lines in the diagram, but let’s not worry about them. They carry no charge.
The point here is that we recognize the charge as being the same charge, even though it is being carried by different particles.
Let’s see how this law applies to the following scenario: We have a closed, isolated, electrically-insulated container. Within the container there is a number Np of protons; as always, they carry one unit of positive charge apiece. There is also a number Ne of electrons; as always, they carry one unit of negative charge apiece. Finally there is a number Nn of neutrons. In this subsection, we temporarily pretend that other types of charge carriers (such as positrons) do not exist.
If the two-fluid model were correct, we would in general need two variables to keep track of the two kinds of charge. In the previous paragraph we used two variables (Np and Ne), but that was to keep track of the particles, not the charge itself.
Let’s make a change of variables. For this system, we define
|
The variable Q has a conventional name: it is called the charge. Equation 1 tells us how to calculate the charge for this system (whereas for a more complicated system a more complicated formula might be needed). The value of Q can be positive, negative, or zero. The law of conservation of charge states that Q is conserved.4
In contrast, the law of conservation of charge says nothing about R. In fact, R has nothing to do with charge, and is not even a conserved quantity. Every time a neutron decays, R increases by two, since the decay produces a new proton and a new electron. The charge Q is conserved during this process, as it must be for any process … but R is manifestly not conserved.
Let’s be clear: we only need one variable, Q, to tell us everything we need to know about charge. Any one-variable model can always be dressed up to look like it has two (or more) variables, but there’s no point in doing so. It would be worse than useless.
Using the two variables Q and R is mathematically equivalent to using the two variables Np and Ne. If you start with Q, that is all you will ever need to keep track of charge; you don’t need R and you don’t need to keep track of Np and Ne separately in order to keep track of the amount of charge.
Of course R is meaningful; for example, an electrically-neutral plasma (Q=0, R≫0) has much greater electrical conductivity than an electrically-neutral vacuum (Q=0, R=0). (A parallel statement can be made concerning solid state physics: A compensated semiconductor is different from an intrinsic semiconductor.) That’s all fine; it simply tells you that there’s more to physics than just charge. Still, the fact remains that the single variable Q represents the charge, and you don’t need to know anything but Q to know the charge.
Now let’s look in more detail at neutron decay. This is relevant because it violates the strong two-component model. Examples include:
The baryon number (aka atomic mass number) A is conserved during beta decay. This is not a consequence of conservation of charge; it is a consequence of another conservation law, namely conservation of baryon number. Combining conservation of A with conservation of Q, we can infer that the quantity R + 2Nn is conserved … but R by itself is not conserved.
If you know A you can predict the molar mass of the atom approximately (but not exactly).
The nature of electrical charge can be understood with even greater clarity when contrasted with the subatomic color charge: There is only one kind of electrical charge, but there are three kinds of color charge.
Terminology: The term “charge” by itself is synonymous with plain old electrical charge. If you want to refer to color charge, you have to say “color charge”.
The symmetry of color charge is described by the group SU(3), while the symmetry of electrical charge is described by the group U(1). This allows us to say with great formality and precision that there are three kinds of color charge but only one kind of electrical charge.
For more on color charge, see reference 5, reference 6, and reference 7.
If we are talking about “the” pressure, there is only one kind of pressure. For example, it appears in the equation
| (2) |
where E is the energy, P is the pressure, V is the volume, T is the temperature, and S is the entropy. It is straightforward to measure the pressure, using a Bourdon tube or otherwise.
However, under some circumstances there is some value in introducing the notion of partial pressure. In a sample of ordinary air, there is some partial pressure of oxygen, some partial pressure of nitrogen, and various smaller contributions.
If you know the various partial pressures, you can predict the overall pressure ... but the converse is not true. The pressure does not care what kind of particles are exerting the pressure. In principle you could measure the partial pressure using a semipermeable membrane plus a Bourdon tube, but this is not very convenient. If you have a mixture of N gases you would need something like N different selective membranes, which is not necessarily easy to arrange.
Similar words apply to charge-carrying particles. The charge does not care what sort of particles are carrying the charge. However, if you have the right kinds of semipermeable membranes, you can sort out the various contributions.
We can make sense of this with the help of Pourbaix diagrams, such as the following, which shows copper in equilibrium with water. The region between the diagonal dashed lines is where water itself is stable; above this region water oxidizes itself and evolves O2; below this region water reduces itself and evolves H2.
Such diagrams come in handy if you are trying to understand
The horizontal axis is pH, which is related to the partial pressure of H+ ions. You can measure pH using a voltmeter with an electrode that is sensitive only to H+ ions, not to any other charge-carrying particles (not even if they contain protons, not even if they contain hydrogen, e.g. NH4+ ions).
The vertical axis is the oxidation-reduction potential (ORP). You can measure it using a voltmeter that responds only to electrons, not to any other charge-carrying particles.
This is what a two-fluid model looks like. It is not a model of charge. It is a model of ORP and pH.
There are innumerable other diagrams of this sort that could be constructed. For example, one could use pOH as one of the axes, instead of (or in addition to) pH.
Very commonly, as soon as you start considering a two-fluid model, you end up with a more-than-two-fluid model.
If we want to be scientific (as discussed in reference 8), due diligence requires that we examine the arguments in favor of the two-fluid model. We did some of this in section 5, but let’s go over it again.
One argument starts from the correct observation that in ordinary terrestrial matter, positive charge is predominantly embodied in protons, while negative charge is predominantly embodied in electrons. This however is not evidence against the one-fluid model, not in the slightest. It fails to prove that there are two kinds of charge. It fails for at least two reasons:
Charge, like other fundamental physical quantities such as energy and momentum, is something of an abstraction. The fact that it is abstract doesn’t make it any less real. (See reference 9 for a discussion of abstract things and embodiments thereof.) We don’t say that momentum embodied in a piece of wood is in any fundamental way different from momentum embodied in a piece of plastic; the embodiment is different, but the momentum is fundamentally the same. By the same token, the charge embodied in electrons is fundamentally the same as the charge embodied in other particles. In particular, negatively-charged pions, muons, antiprotons, etc., do not “contain” electrons. They contain negative charge, but they do not contain electrons. Conversely, there are a lot of things we know about an electron, including mass, lepton number, charge, et cetera. So we see that the concept of charge and the concept of electron are very different. Charge is just one property of the electron, one property among many.
This supports the crucial point of today’s discussion: If there were two kinds of charge (apples and oranges), you would need two numbers to describe the state of charge ... but this is never observed. You never need more than one number to describe the charge of any given object or region. To describe an electron you need more than one number, but that’s the answer to a different question. In particular, an electron is different from an antiproton, even though they have the same charge.
It’s a mistake to overemphasize the embodiments and/or the mobility of the embodiments. In a sample containing a mixture of five acids, there will be six different kinds of current. That alone should suffice to invalidate all the arguments in favor of a two-fluid model; if you’re going to allow more than one, logic requires you to allow an unlimited number.
The smart way to proceed is to say that there is only one kind of charge, just as there is only one kind of momentum. The momentum is the same kind of momentum, no matter whether it is embodied in electrons, protons, wood, plastic, or whatever. By the same token, the charge is the same kind of charge, no matter whether it is embodied in electrons, protons, ions, subatomic particles, or whatever.
Charge is not matter, and matter is not charge. If you mean “charge”, you should say “charge”, while if you mean “charged particle”, you should say “charged particle”. There exist many kinds of charged particles, but only one kind of electrical charge.
The situation is shown in figure 5.
| Within a given column, the entities on different rows have possibly different solubility, different lifetime, different mass, et cetera. | Within a given column, the entities have the same charge. |
| To keep track of many things, we need many numbers. | To keep track of charge, we need only one number. |
It would be unwise to even mention the two-fluid model in an introductory course. There is nothing to be gained from it. In general, mentioning a misconception is more likely to reinforce it than to dispel it.
Introductory courses often explore the topic of electricity by means of simple macroscopic experiments. These may include rubbing a rubber rod on fur or peeling bits of cellophane tape off the desktop, then testing for the presence of charge using home-made electroscopes. Alas, this does not provide any evidence for or against the two-fluid model or the one-fluid model. Even the fallacious arguments mentioned in section 9 are irrelevant in such a situation, because they involve microscopic phenomena that cannot be perceived by casual macroscopic observation.
However, there is more to physics than simple macroscopic experiments; there is also theory, and there are more advanced experiments. There are multiple ways to discriminate between the various hypotheses.
In an introductory class, there is no need to emphasize the one-component model, nor to refute the two-fluid model, nor even to mention the two-fluid model (unless a student brings it up). The sensible approach is just to introduce the idea of “charge”, say that the amount of charge Q can be positive, zero, or negative, and proceed from there. This is the approach taken by some textbooks (e.g. reference 10). There is no need to make things more complicated than that. The simple and obvious answer is the fundamentally correct answer.
It’s amazing how many introductory physics books get this wrong: reference 11, reference 12, reference 13, and reference 14 among others.