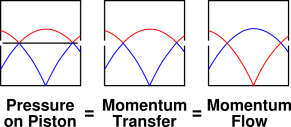
Figure 1: Pressure, ± Piston ± Collisions
It is important to realize that in fluids (including water and air) there is pressure everywhere. Pressure is not something that happens only when the fluid hits a tangible surface.
Yes, pressure is force per unit area. But we can get a more sophisticated notion of pressure if we restate that as momentum flow across the area.
Force is just momentum flow. (The net force is the momentum flow from A to B minus the momentum flow from B to A.)
Pressure is just one contribution to the momentum flow. There are other contributions to the momentum flow, notably from the shear viscosity and the bulk viscosity. We will not have much to say about viscosity, except to say: (a) It is trickier than you might imagine to give a simple, non-mathematical way of distinguishing pressure from bulk viscosity effects; the simple explanations are not correct, and the correct explanations are not simple. (b) There are many practical situations where the effects of viscosity are small compared to other effects, especially when we are interested in large objects moving quickly through ordinary not-especially-viscous fluids.
Temporarily, for simplicity, let’s assume the viscosity is very small, and talk only about pressure.
Figure 1 shows three different cases, i.e. three different ways that momentum can be carried from parcel A to parcel B. All three ways are called pressure.
In each case, have some gas in a box. The trajectory of one gas particle is shown in red. The trajectory of another gas particle is shown in blue. The box itself is shown in black. Everything is in equilibrium. The pressure in the top of the box is less than the pressure in the bottom of the box, because a gravitational field is acting on the gas. Gravity is causing a downward force on the gas particles, as you can see from the fact that the trajectories are not straight but rather parabolic everywhere (except for collisions).
The gas is in equilibrium because the gravitational force is balanced by an upward force due to the pressure gradient, as we now discuss.
In the left third of the diagram, there is a piston in the box. There is no net force on the piston, because the force due to the blue particle hitting the bottom of the piston is balanced by the force of the red particle hitting the top of the piston. Even though the net force is zero, there is some flow of momentum, i.e. stress. There is a downward flow of downward momentum (or equivalently an upward flow of upward momentum).
In the middle third of the diagram, momentum is being transferred in a different way. There are two places where the blue particle hits the red particle, transferring momentum across the boundary between top and bottom. The boundary is intangible, but it is still a boundary. This momentum transfer is called pressure, even though there is no tangible surface for the pressure to act upon.
On the right third of the diagram, the piston is absent and even the collisions are absent. The two particles don’t collide – they just fly past each other. The momentum flow is the same! It is still true that the pressure in the bottom is larger because of gravity, and it is still true that momentum is being transferred from bottom to top because of the pressure gradient.
In all three cases, one particle or the other turns around when it collides with the bottom of the box. This this collision is how pressure acts on the bottom surface. Also in all three cases, one particle or the other turns around near the top of the box due to gravity, without hitting the top of the box. That represents the fact that at the top of the box there is very little pressure. In all cases the net effect of all the collisions can be summarized as a transfer of momentum from the gravitational field to the bottom of the box.
This notion of "flow" is central to what we mean by conservation; see reference 1.
Momentum flow is how you derive the equations of fluid dynamics; see reference 2.
All this generalizes beautifully to D=3+1 spacetime; see reference 3 Chapter 5.
Disclaimer: It is usually better to think of a fluid as a continuous fluid with macroscopic properties such as pressure, temperature, viscosity, et cetera ... rather than as a collection of individual particles. The macroscopic properties are ultimately derivable from the particle dynamics, as we have done here, but the derivation is laborious and error-prone, so don’t go there unless you really need to.
In macroscopic terms, our results can be stated quite simply: the fluid has pressure everywhere, not just when it acts on a tangible surface. The force on a small parcel of fluid depends on the gradient of the pressure.