1  Introduction

Obviously you can’t learn (or teach) everything at once ... but you have to start somewhere. This leads to two important questions: (1) where to start, and (2) when to move on to the next topic.

To answer such questions, the only thing that has ever made sense to me is the following:

Spiral approach: Learn a few rough ideas, then spiral back, making connections between the ideas. Then keep spiraling back again and again, gradually adding new ideas, refining the ideas, and making more connections, checking to see in what ways each idea is consistent (or inconsistent!) with the others.

Therefore the answer to question (1) is that the starting-point doesn’t matter very much. After a few trips around the spiral, nobody knows or cares where it started.

Question (2) is super-important, because it will come up again and again, every day for the rest of your life. Each time, the spiral approach provides a partial (but not complete) answer. It says that you do not need to master one topic before moving on to the next. Plan on coming back.

The spiral approach stands in contrast to the 2000-year-old axiomatic / deductive approach, where topics are arranged in some monotonic order, and the student is expected to master each topic before moving on to the next. As discussed in section 4, the axiomatic approach is a bad idea. The more rigidly it is applied, the worse it is. It may seem elegant or rigorous, but it is not the way people learn or think.

*   Contents

• 1  Introduction
• 2  Some Preliminary Examples
  • 2.1  Long Multiplication
  • 2.2  Equivalent Circuits
• 3  Good: Spirals, Stair-Steps, Tapestries, Building Blocks, Mazes, and Indirect Solutions
  • 3.1  Peek at the Big Picture
  • 3.2  The Spiral Approach
  • 3.3  The Stair-Step Approach
  • 3.4  Tapestries
  • 3.5  The Building-Block Approach
  • 3.6  Mazes
  • 3.7  Multiple Solutions and Indirect Solutions
• 4  Bad: Traditional Axiomatic Approach
• 5  Expertise versus Automaticity
  • 5.1  The Bone Analogy
  • 5.2  Professionals versus Automatons
• 6  Showing the Work, versus Polish
• 7  Appendix
  • 7.1  Don’t Mock the Student
  • 7.2  Cockamamie Circuit
• 8  References

2  Some Preliminary Examples

2.1  Long Multiplication

Suppose somebody wanted to learn long multiplication before they had fully mastered basic short multiplication facts, aka the “times tables”.

That’s actually not a problem. In the worst case, if they had to refer to an actual non-metaphorical 10×10 short-multiplication table while doing their long multiplication exercises, it would not be the end of the world. It would slow them down, but not fatally.

Forsooth, the shoe is pretty much on the other foot: Doing a bunch of long-multiplication problems provides opportunities, motivations, and reasons to learn the basic short-multiplication facts.

The point here is simple: It is absolutely not necessary to master things at one level before moving on to the next level. Any topic of real importance will come up again and again, in various natural contexts, so there will be lots of opportunities to refine the ideas. This is sometimes called successive refinement. It is also called the spiral approach.

2.2  Equivalent Circuits

Consider the following two-part story:

1. At one school, the professor walked into the room and drew three diagrams.

   Figure 1: Thévenin Equivalent Circuit		Figure 2: Norton Equivalent Circuit

   
   Figure 3: Load Line of a Linear Circuit

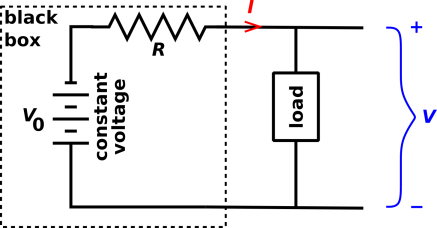
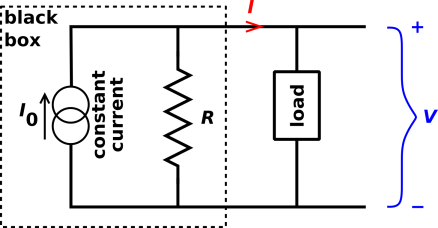
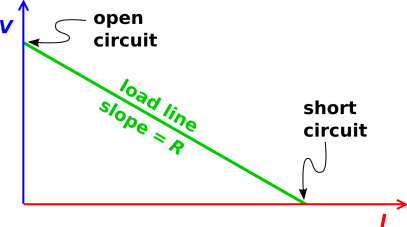
   Pointing to various features of the diagrams, he said something like “Open-circuit voltage, short-circuit current, linear circuit, two points determine a line. Thévenin equivalent, Norton equivalent. Same black-box behavior. Useful. Know it.”

   The whole presentation took only a minute or two. Nothing more needed to be said that day. Many of his sentences didn’t even have verbs. In particular, he did not take time to make sure that the students mastered the concept before moving on.

   The students looked at his diagram and nodded. Open-circuit voltage. Short-circuit current. Two points determine a line. Sounds reasonable. Sounds useful.

   In the unlikely event that some student initially acquired a defective understanding of such circuits, that defect would have been cured naturally sooner or later, probably sooner, because equivalent circuits are indeed useful, and get used again and again and again. One of my favorite sayings is:

   Utility is the best mnemonic.

   That is to say: Stuff that gets used gets remembered.

2. At another school, the same subject was handled very differently. The professor lectured on and on about Thévenin equivalents, Norton equivalents, wye-delta transformations, blah blah blah ... for 90 minutes! He figured it was an important topic, and he wanted to make sure everybody understood it before moving on.

   Just to make double-especially sure everybody understood it before moving on, he assigned hours of homework on the subject. Students were required to analyze some cockamamie circuit with lots of resistors and lots of batteries.

   Just to make triple-extra sure that everybody understood it before moving on, there was a big lab assignment. Students were required to actually build the cockamamie circuit and measure it, comparing against the Thévenin and Norton predictions. For at least two idiotic reasons (as discussed in section 7.2) the observations did not match the predictions.

   The upshot was that these students came away with the idea that Thévenin and Norton equivalents were horribly complicated and useless.

So you see, the two schools led their students to dramatically different conclusions.

The point of this parable is simple: It is absolutely not necessary for students to master an idea before moving on. Instead, one can use the spiral approach: Introduce the subject lightly, then move on to other topics, then come back and revisit each topic, tying everything together. If the supposedly-important ideas really are important, they will come up again and again, in the normal course of business.

As the travel guidebooks say: When planning a trip to the big city, do not plan on seeing every single museum on your first trip. Assume you will come back. Assume your first trip is not the only trip.

3  Good: Spirals, Stair-Steps, Tapestries, Building Blocks, Mazes, and Indirect Solutions

3.1  Peek at the Big Picture

Most of this article is about how to take a complex topic apart and then, later, put it back together. However, in some situations, especially with students who are seeing the topic for the first time, it pays to provide some sort of overview / survey / synopsis.¹ This is analogous to peeking at the picture on the box that the jigsaw puzzle came in. It provides some perspective and some indication of how the various pieces fit into the big picture. This helps motivate folks to learn about the pieces.

This involves some tricky judgment calls, because there are limits. Sometimes the big picture can be intimidating and overwhelming.

3.2  The Spiral Approach

When it comes to learning (and teaching), it doesn’t pay to worry too much about the order in which ideas are presented.

Instead, it makes sense to use a spiral approach. That is, we start by mentioning a bunch of rough ideas, including some applications as well as some fundamental building-blocks. Then we go over everything again, making connections between the ideas, refining the ideas, discussing things in more depth, and introducing some new ideas. And so on, iteratively.

By the time you have made the Nth turn around the spiral, nobody cares – or even remembers – where you started.

See reference 1 for an insightful discussion of how thinking and problem-solving are done. This includes an interesting specific example, namely proving the unique-factorization theorem ... but the process is even more interesting than the result. Also reference 2 is a classic, highly-regarded discussion of problem-solving techniques. Additional discussion can be found in reference 3.

3.3  The Stair-Step Approach

I like to tell students:

You’re not Superman, and I’m not Superman either. I can’t teach you how to leap tall buildings in a single bound. I can however show you where the stairwell is. We can get to the top one step at a time.

Figure 4: Long Spiral Staircase

3.4  Tapestries

Feynman compared knowledge to a grand tapestry. Any unknown fact is like a hole in the tapestry. The hole can be repaired by weaving upward from the bottom, downward from the top, or inward from the sides. I would go even farther and point out that you can start in the middle of empty space and weave new fabric from scratch, and then patch it into to the main tapestry later. Furthermore, real problem-solving involves a great deal of exploring avenues that turn out to be dead ends, and then back-tracking.

Actually there are even more options than that, because the network of knowledge is very high-dimensional, not just two-dimensional like a tapestry. Ideas are connected in many, many different directions.

3.5  The Building-Block Approach

When teaching real-world skills, it is essential to use the building-block approach. That is, we break the overall task into modules, into small building-blocks. Then we teach a few of the blocks in isolation, and then gradually combine them, two at a time, then three at a time, et cetera. Then we spiral back and add a few more blocks. Eventually we combine everything to create the final complete edifice.

The wise teacher will not only use this approach, but explain the process, so that students can internalize it. That is to say, the topic of problem-solving skills is worth discussing explicitly. Later, when they are on their own, when they encounter a hard problem, students will be prepared to chip away at it, breaking it into a large number of manageable sub-problems, and then combining the sub-results.

The final step – putting things together – must not be omitted. Dealing with the blocks one by one is a fine place to begin, but it is not an acceptable place to end!

3.6  Mazes

The maze metaphor is discussed in reference 4.

Figure 5: Maze, as a Metaphor for How Research is Done

3.7  Multiple Solutions and Indirect Solutions

As a general rule:

With rare exceptions, the teacher should not require that a problem be solved a particular way. Non-standard methods should be tolerated, within reason. There is a continuum, ranging from creative, indirect, roundabout, or peculiar to outright bizarre and perverse.

If you want to give students practice with a particular method, choose examples where that method is clearly preferable. If the method is any good, such examples should be easy to find.

For the next level of detail, see reference 5.

4  Bad: Traditional Axiomatic Approach

The spiral approach is dramatically different from what might be considered the “traditional” axiomatic approach. Consider the following contrast:

Furthermore: Just because the straight-forward approach is bad does not mean that the straight-backward approach is good. As usual, all the extremes are wrong. For learning and teaching, some version of the spiral approach and/or the building-block approach is usually a good idea, as discussed in section 3.2 and section 3.5. In a more general problem-solving situation, where there is no teacher (i.e. no one who knows what the right answer is) the situation is even more fluid. You have to come at the problem from many different angles.

5  Expertise versus Automaticity

5.1  The Bone Analogy

Some folks (including Sal Khan) argue against the spiral approach. They assert that it is vital to achieve a a «solid» understanding of one topic before moving on to the next. They consider a non-solid understanding to be dangerous. Khan explicitly compares it to a broken bone.

I apply the bone analogy differently: Real bones have hollow parts and, even more remarkably, cancellous parts, as shown in figure 6 (from reference 6).

Figure 6: Cancellous Bone

Cancellous bones (aka cancelate bones) work better than any corresponding «solid» bone would work, in terms of strength-to-weight ratio, growth rate, and other critical measures. Non-metaphorically speaking, even if you think a «solid» understanding is the ultimate goal, it is better to lay down a preliminary cancellous structure, and then spiral back to fill in whatever gaps really need filling. In terms of pedagogical sequencing, the only thing that has ever made sense to me is the spiral approach. Don’t assume that the first exposure to a topic will be the last.

5.2  Professionals versus Automatons

Here’s another example, namely US Airways flight 1549, the one that ended up in the Hudson River. This is a case where we can sharply compare automaticity versus expertise and professionalism.

Take a guess: Who saved the day? The automatons, or the professionals????

1. The autopilot was not turned on at the time of the bird strike. The First Officer was hand-flying the plane. The pilots could have turned on the autopilot, but they didn’t bother, and it would not have made much difference either way. It would’ve taken about the same amount of effort to tell the autopilot what do as to just do it by hand. If they had switched it on, they would have had to switch it off about a minute later.
2. The GPWS was turned on by default, as usual. It got left on. All it did was generate unhelpful nuisance warnings. In the aftermath, the NTSB recommended adding to the emergency checklist an item about turning off the GPWS. That’s serious business. You don’t lightly add items to an emergency checklist.
3. The alpha-protect system was on and could not be turned off. The A320 is a fly-by-wire aircraft, and the computer gets the final say. It made things worse: In the last seconds of flight, the pilot commanded the plane to raise the nose another degree or so and the airplane did not respond, because the alpha-protect system would not allow it.

In summary, I score the automatons 0-2-1: No wins, two losses, and one tie.

Now what about the pilots? Do you think they were drill drill drilled to achieve “automaticity”? If so, you do not understand the job. Really not.

Sure, they were trained to know the emergency checklists by rote ... but they were also trained to understand every item on the list at a much deeper level. The two types of learning are not mutually exclusive. All of the rote stuff the First Officer knew was unnecessary in this case, because he had the Quick Reference Handbook to follow. What’s more, virtually all of the QRH was irrelevant! The engine-restart procedures assumed the engine quit at altitude, allowing plenty of time for a restart. Step 3 on the checklist involved waiting for 30 seconds. Think about that. The total time from bird strike to touchdown was one minute and 15 seconds. The First Officer skipped the 30-second wait step. An automaton would not have. On the other hand, he never made it past step 4, because both engines were completely ruined. (He had no way of knowing they were ruined, so it made sense to attempt the restart.)

They crew didn’t even make it as far as step 0 of the ditching checklist ... and wouldn’t have been able to complete the checklist anyway. And no automaton could have done better. An automaton can only do what it is programmed to do, and nobody had ever contemplated making a ditching decision on such short notice.

So this is why you need experts and professionals. They went off-script. Waaaay off-script. I’ll concede the pilots exhibited “some” elements of more-or-less “automatic” behavior. For example, the autopilot could have kept the aircraft right-side-up, automatically. The pilot was able to do the same thing, subconsciously, “automatically” if you will ... but that’s not the interesting part of the story. The interesting part is all the non-automatic stuff he was doing at the same time.

Sure, those guys were experts. They were well trained. However, the objective and result of the training was not automaticity. Not even close.

6  Showing the Work, versus Polish

Here’s another set of contrasts for you:

Let’s be clear: Listening to a piano sonata is one thing. Performing one is something else entirely. Composing one is something else yet again.

I mention this because in some fields, the textbooks tend to be elegant and highly polished. This has been the practice for thousands of years, continuing to the present day. They discuss the most elegant solution, without discussing how the solution was actually found, i.e. the messy process of proceeding upward from the bottom, downward from the top, inward from the sides, and outward from the middle, with lots of back-tracking, finding an inelegant solution and then gradually refining it.

In the real world, in any sort of engineering situation, you are required to show the work. That includes keeping the scaffolding in place, or at least keeping it close at hand. This is often not easy to do, but it is required so that others can validate, maintain, repair, reuse, and extend your work. For the next level of detail, see reference 7.

7  Appendix

7.1  Don’t Mock the Student

According to legend (as quoted in reference 8), a new student of Euclid’s once asked him, “What shall I get by learning these things?” In reply, Euclid beckoned his slave and told him, “Give him a coin, since he must make gain out of what he learns”.

This is a horrifying story. A student who asks what something is good for should be encouraged. A student who asks how something fits into the big picture should be encouraged. Teachers should be prepared to answer such questions. Euclid may have been a good mathematician, but in my opinion he was not a good teacher, if the legend is to be believed. In any case, apart from the legend, Euclid’s book says almost nothing about motivations or applications.

7.2  Cockamamie Circuit

In case you were wondering how it was possible to screw up something so simple as Thévenin and Norton equivalents, as discussed in section 2.2, here’s next level of detail.

The school was too cheap to buy 1% precision resistors, which cost about a penny apiece. They thought their students didn’t deserve that kind of luxury. So they used 10% resistors instead. The cockamamie circuit contained a large number of resistors, so the uncertainties accumulated. What’s worse, the assignment required students to measure a voltage that was a small difference between large numbers, which made the relative uncertainty enormous.

Secondly, although the homework calculation used ideal batteries as voltage sources, the lab project used bench power supplies. It turns out that a battery puts out a more-or-less constant voltage over a wide range of positive and negative currents, whereas an electronic power supply does not tolerate negative currents. As Murphy’s Law would have it, the cockamamie circuit was trying to run negative current through one of the power supplies. So the observed behavior of the circuit bore absolutely no resemblance to the homemwork calculation.

8  References

1.

Timothy Gowers,
“Proving the fundamental theorem of arithmetic”
https://gowers.wordpress.com/2011/11/18/proving-the-fundamental-theorem-of-arithmetic/

2.

George Pólya,
How to Solve It: A New Aspect of Mathematical Method
1st edition (1945), 2nd edition (1957), Princeton University Press

3.

John Denker,
“Principles of Teaching and Learning”
www.av8n.com/physics/pedagogy.htm

4.

John Denker,
“How Research is Done : Exploring a Maze using only Local Information”
www.av8n.com/physics/research-maze.htm

5.

John Denker,
“Taking an Indirect Approach”
../education/indirect-approach.htm

6.

medicalpicturesinfo.com,
“Cancellous Bone”
http://medicalpicturesinfo.com/wp-content/uploads/2011/09/Cancellous-Bone-4.gif

7.

John Denker,
“Suggestions for Writing Good Software”
../computer/htm/good-software.htm

8.

Marvin Jay Greenberg,
Euclidean & Non-Euclidean Geometries: Development and History
2nd edition, W.H. Freeman and Co., New York (1973) pp. 7-8.

1

It’s odd that English has three words that mean exactly the same thing.